基于matlab的控制系统与仿真-3
Author:AXYZdong 自动化专业 工科男
有一点思考,有一点想法,有一点理性!
定个小小目标,努力成为习惯!在最美的年华遇见更好的自己!
习题3
3.3 绘制以下传递函数模型的单位阶跃响应曲线
>>sys=tf([5 8],[1 4 6 3 3])
sys =
5 s + 8
-----------------------------
s^4 + 4 s^3 + 6 s^2 + 3 s + 3
Continuous-time transfer function.
>> step(sys)
运行结果:

3.7 绘制以下系统的根轨迹曲线
(1)
(2)
G1= tf([1],conv([1 0],conv([1 2 2],[1 6 13])))
G1 =
1
------------------------------------
s^5 + 8 s^4 + 27 s^3 + 38 s^2 + 26 s
Continuous-time transfer function.
>> rlocus(G1)
>> G2= tf([1 12],conv([1 1],conv([1 12 100],[1 10])))
G2 =
s + 12
--------------------------------------
s^4 + 23 s^3 + 242 s^2 + 1220 s + 1000
Continuous-time transfer function.
>> rlocus(G2)

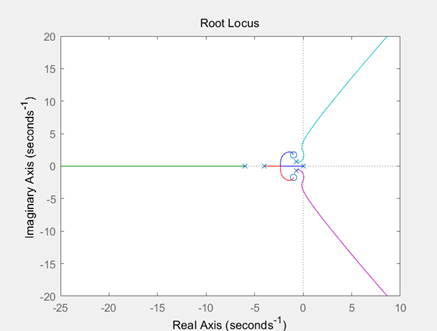
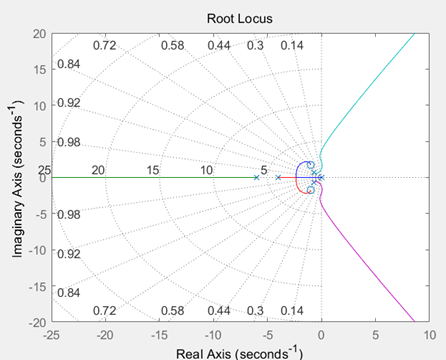
3.8 已知反馈系统的开环传递函数为:
试画出系统的根轨迹和根轨迹渐近线。
>> G3= tf([1 2 4],conv([1 0],conv([1 4],conv([1 6],[1 1.4 1]))))
G3 =
s^2 + 2 s + 4
-----------------------------------------
s^5 + 11.4 s^4 + 39 s^3 + 43.6 s^2 + 24 s
Continuous-time transfer function.
>> rlocus(G3)
>> sgrid
3.9 已知单位反馈控制系统的开环传递函数为:
试画出下列两种情形的根轨迹图;
(1)负反馈控制系统的根轨迹图;
(2)正反馈控制系统的根轨迹图;
>> G4= tf([1 2],conv([1 0],conv([1 4],conv([1 8],[1 2 5]))))
G4 =
s + 2
---------------------------------------
s^5 + 14 s^4 + 61 s^3 + 124 s^2 + 160 s
Continuous-time transfer function.
>> rlocus(G4)
>> rlocus(-G4)

▲ 负反馈

▲ 正反馈
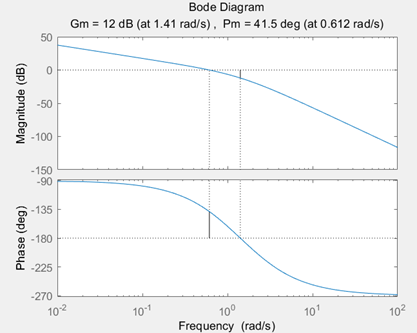
3.10 已知某控制系统的开环传递函数
当 时,试绘制系统的开环频率特性曲线,并求出系统的幅值裕量与相位裕量。
G5=zpk([],[0 -1 -2],1.5)
G5 =
1.5
-------------
s (s+1) (s+2)
Continuous-time zero/pole/gain model.
>> margin(G5)
>> [Gm,Pm,Wcg,Wcp] = margin(G5)
Gm =
4.0000
Pm =
41.5340
Wcg =
1.4142
Wcp =
0.6118
3.11 已知一个典型的二阶环节传递函数为
其中 ,试分别绘制 时的 Bode 图。
wn=0.7;
s=tf('s');
n=[0.1,0.4,1.0,1.6,2.0];
for i=n
figure
G=wn^2/(s^2+2*i*wn*s+wn^2);
bode(G);
end


▲ 从上到下$\zeta=0.1、0.4、1.0、1.6、2.0$
3.13 已知系统开环传递函数为
试求出 Nyquist 曲线。
>> G=zpk([-1],[-0.8-1.6*j,-0.8+1.6*j],3)
G =
3 (s+1)
------------------
(s^2 + 1.6s + 3.2)
Continuous-time zero/pole/gain model.
>> nyquist(G)

3.14 已知二阶系统传递函数为:
试绘制阻尼系数 分别为 时的系统的 Nyquist 曲线。
n=[0.4,0.7,1.0,1.3];
for i=n
figure
G=tf([0 1],[1 2*i 1]);
nyquist(G);
end


▲ 从上到下$\zeta=0.4、0.7、1.0、1.3$
本次的分享就到这里

好书不厌百回读,熟读自知其中意。将学习成为习惯,用知识改变命运,用博客见证成长,用行动证明努力。
如果我的博客对你有帮助、如果你喜欢我的博客内容,请 “点赞” “评论” “收藏” 一键三连哦!
听说 👉 点赞 👈 的人运气不会太差,每一天都会元气满满呦!^ _ ^
**码字不易,大家的支持就是我坚持下去的动力。点赞后不要忘了👉关注👈我哦!
如果以上内容有任何错误或者不准确的地方,欢迎在下面👇留个言。或者你有更好的想法,欢迎一起交流学习~~~
- 点赞
- 收藏
- 关注作者


评论(0)