LAPJV算法学习笔记

伪代码：

LAPJV算法详解（ing_Sparse Direction的博客-CSDN博客_lap.lapjv

  

   

    

     

    
    

     

      from lapjv import lapjv
     
    
   

    

     

    
    

     

      import numpy as np
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      a = np.array([[0.1,0.6,0.3],[0.2,0.1,0.6],[0.5,0.2,0.9]])
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      x,y,c = lapjv(a)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      print(x,y,c)
     
    
  
 

out: [2 0 1] [1 2 0] (0.699999988079071, array([0. , 0.3, 0.4], dtype=float32), array([-0.10000002, -0.2 , 0.3 ], dtype=float32))

其中x,y分别是按照 行列来计算的

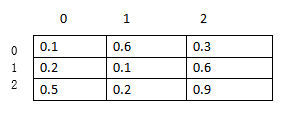
行索引分配[2,0,1]: cost = 0.3+0.2 +0.2 = 0.7

0行，2列

1行，0列

2行，1列

列索引分配 [1,2,0]：cost = 0.2 + 0.2 +0.3 =0.7

0列，1行

1列，2行

2列，0行

cost就是求和最小。

bytetrack用到的lapjv算法：

  

   

    

     

    
    

     

        cost, x, y = lap.lapjv(cost_matrix, extend_cost=True, cost_limit=thresh)
     
    
   

    

     

    
    

     
    for ix, mx in enumerate(x):
     
    
   

    

     

    
    

     
        if mx >= 0:
     
    
   

    

     

    
    

     

                  matches.append([ix, mx])
     
    
  
 

c++版：

参见博客：

ByteTrack 多目标跟踪 测试笔记_jacke121的专栏-CSDN博客

在bytetrack的c++版本中。

网友实现的python3源码版：

LAPJV-线性分配问题的Jonker-Volgenant算法V3.0：解决LAP的Jonker-Volgenant算法的Matlab实现。-matlab开发_-互联网文档类资源-CSDN下载

文章来源: blog.csdn.net，作者：AI视觉网奇，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/jacke121/article/details/122478422