背景
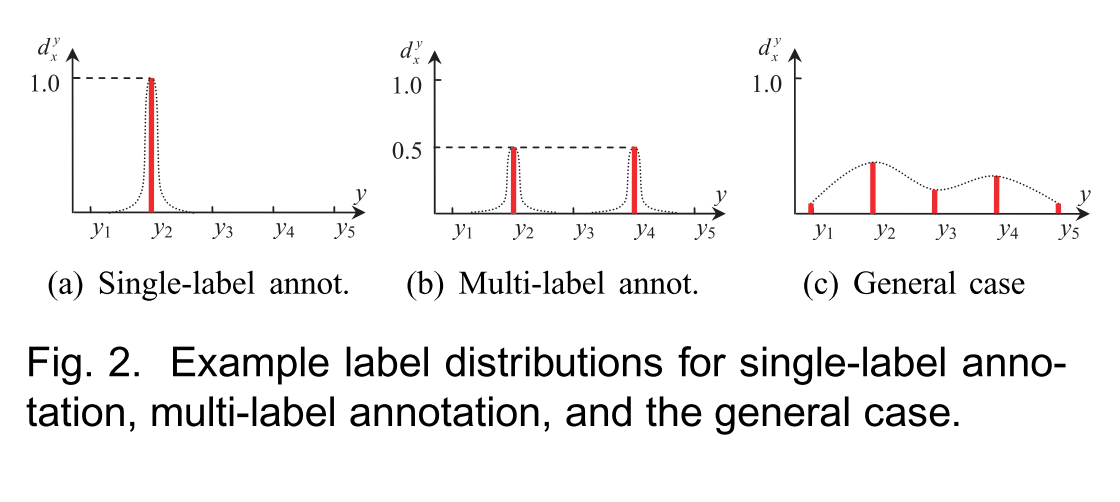
学习的本质是构建从实例到标签的映射关系,但有时候标签存在模糊性,即一个实例不一定映射到一个标签,现有的学习范式中,主要存在两种形式——单标签学习和多标签学习。单标签学习是指给一个实例分配一个标签,多标签学习是指给一个实例分配多个标签。
以上两种形式都在回答一个问题:“哪个(哪些)标签可以描述这个实例”,但都没有回答一个问题是“每个标签能够在多大程度上描述这个实例”,也就是每个标签之间相对的重要程度。
假设对于一个实例
x,分配一个实数
dxy 描述
y描述
x的程度。一般
dxy∈[0,1],如果这个标签集是完整的,标签集合里面的标签总是能够完整的描述实例,则存在
∑ydxy=1.
对于一个实例,所有标签的描述程度构成一个类似于概率分布的数据形式,称为标签分布。
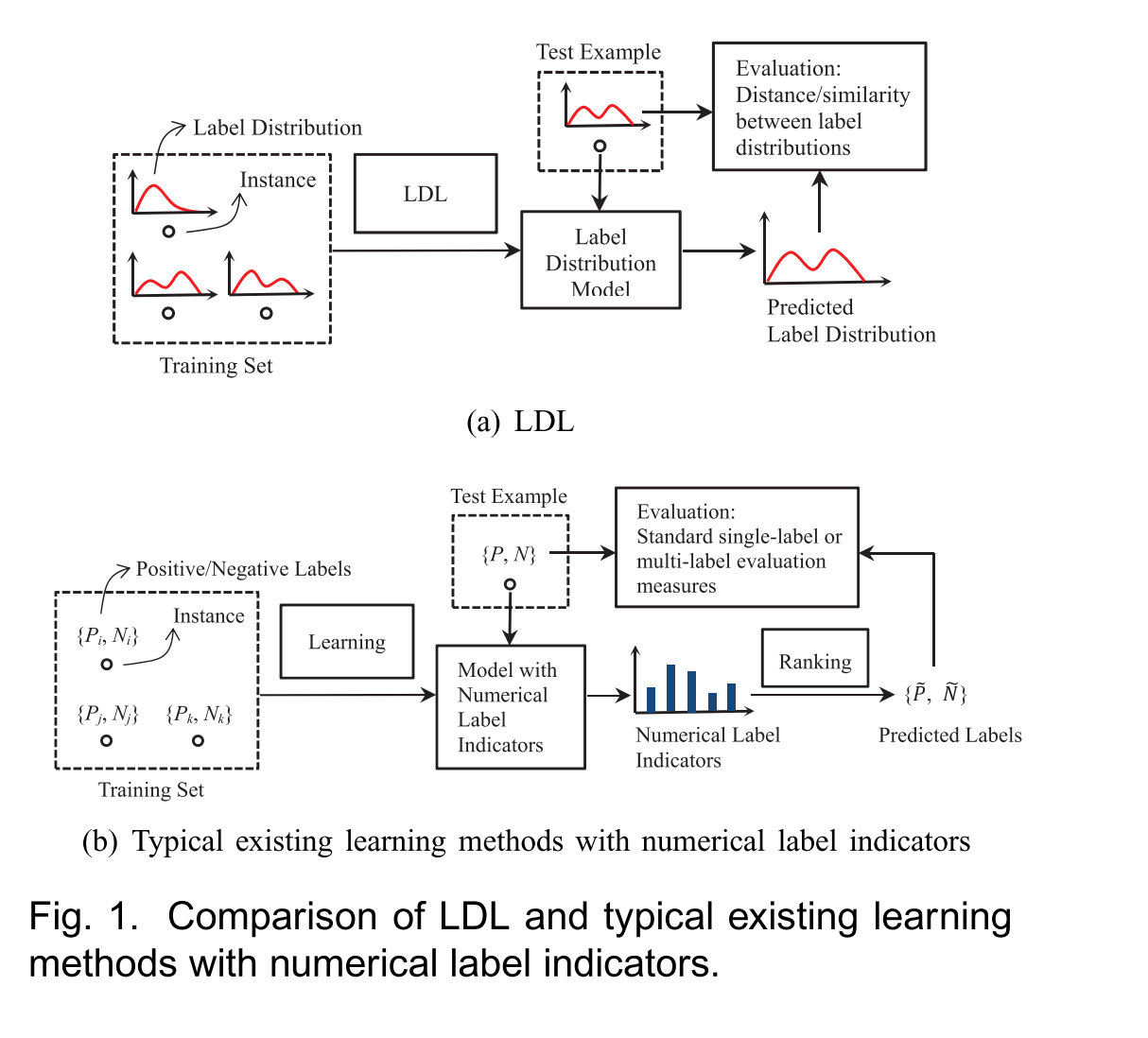
与传统学习范式

-
每个LDL实例都与标签分布明确相关,而不是单个标签或相关标签集,标签分布的标签来自于原始数据,是原始数据的一部分,而不是人为地从原始数据生成的。
-
以前的学习范式通过对预测结果进行排序,根据顺序决定。只要排名不变,标签的值不是很重要;LDL关心的是整体的标签分布,每个标签的描述程度的值是很重要的。
-
以往的SLL和MLL的评价指标是通用的;LDL的性能通过预测标签分布和真实标签分布之间的相似性或距离和评估。
问题定义

由上图可知,LDL是SLL和MLL更普遍的情况,SLL和MLL可以看作是LDL的特殊情况。
LDL意味着更大的输出空间,SLL的输出可能性是标签的个数
c,MLL的输出可能性是
2c−1,LDL的输出值只需要满足
dxy∈[0,1] 和
∑ydxy=1,意味着无数种可能性。
问题定义如下:
输入空间为
X=R2,完整标签集合为
y=y1,y2,...,yc,给定一个训练集
S=(x1,D1),(x2,D2),...,(xn,Dn),LDL的目标是学习一个条件概率密度函数
p(y∣x),其中
x∈X,y∈Y。
利用
p(y∣x;θ)表示参数模型,
θ 表示模型参数,对于输入训练集
S,找到参数
θ 使得模型生成的分布与实际分布
Di 相似。
如果采用KL散度度量两个分布的相似性,那么最优的模型参数
θ∗的公式为:

对于SLL,上式变为

对于MLL,则上式为

评价指标

KL散度
距离度量:香农信息熵家族,信息熵偏差测量
Dis(D,D^)=j=1∑cdjlndj^dj
dis = np.sum(real * np.log(real/predict))
Chebyshev
切比雪夫距离:距离度量,属于 L_p 闵氏距离家族
Dis(D,D^)=maxj∣dj−dj^∣
真实分布与预测分布标签之间差值的最大值
dis = np.sum(np.max(np.abs(real-predict) , 1)) / batch_size
Clark
克拉克距离:距离度量,属于 Squared L_2 家族,以平方的欧几里得距离做为被除数
Dis(D,D^)=c∑j=1c(dj+dj^)2(dj−dj^)2
因为该度量值与标签的种类数有关,为标准化,除以标签数量的平方根。
numerator = np.sum( (real-predict)**2 / (real+predict)**2, axis=1)
denominator = c
dis = np.sum(np.sqrt(numerator/denominator)) / batch_size
Canberra
堪培拉距离:距离度量,属于 L_1 家族,矢量空间中的点对之间的距离的数值度量,它是L_1距离的加权版本。
Dis(D,D^)=c∑j=1cdj+dj^∣dj−dj^∣
该度量值与标签的种类数有关,为标准化,除以标签的数量。
numerator = np.sum( np.abs(real-predict) / (real+predict), axis=1)
denominator = c
dis = np.sum(numerator/denominator) / batch_size
Cosine
余弦距离:相似性度量,属于 Inter Product 家族,是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。
Sim(D,D^)=∑j=1cdj2
∑j=1cdj^2
∑j=1cdjdj^
numerator = np.sum(real*predict, axis=1)
denominator = np.sqrt(np.sum(real**2, axis=1)) * np.sqrt(np.sum(predict**2, axis=1))
sim = np.sum(numerator / denominator) / batch_size
Intersection
交叉距离:相似性度量,最小轨道交叉距离,是天文学中用于评估天文物体之间潜在的近距离接近和碰撞风险的度量。它被定义为两个物体的密切轨道的最近点之间的距离。
Sim(D,D^)=j=1∑cmin(dj,dj^)
真实分布与预测分布标签之间差最小值的和
min_value = np.min(np.dstack(real, predict), axis=-1)
sim = np.sum(min_value) / batch_size
SquareChord
Squared-chord 家族,在量子信息理论中,量子态“接近”的度量。
Dis(D,D^)=j=1∑c(dj
−dj^
)2
sum_value = (np.sqrt(real) - np.sqrt(predict))**2
dis = np.sum(sum_value) / batch_size
Sorensen
L1家族,用于准确测量绝对差异的特征。
Dis(D,D^)=∑j=1c(dj+dj^)∑j=1c∣dj−dj^∣
numerator = np.sum(np.abs(real - predict), axis=1)
denominator = np.sum(real + predict, axis=1)
dis = np.sum(numerator/denominator) / batch_size
KL散度的理解
对于离散信源
X={x1,x2,x3,……,xn},对应的概率为
pi=p(X=xi)
- 自信息量
I(xi)=log(p(xi)1)
- 信息熵
H(X)=−i=1∑np(xi)logp(xi)
交叉熵
对于两个离散变量,设其概率分布为
p(x)和
q(x),其交叉熵的定义为
H(p,q)=x∑p(x)logq(x)1=−a∑p(x)logq(x)
信息论,表示对预测分布
q(x)用真实分布
p(x)进行编码所需的信息量的大小。
KL散度(相对熵)
由交叉熵推出相对熵
DKL(p∣∣q)=H(p,q)−H(p)=−a∑p(x)logq(x)−a∑−p(x)logp(x)=−a∑p(x)(logq(x)−logp(x))=−a∑p(x)logp(x)q(x)=a∑p(x)logq(x)p(x)
由期望推导
本质上,KL散度计算对原始分布中数据概率与近似分布之间的对数差的期望,近似一个分布与实际分布时损失了多少信息。
DKL(p∣∣q)=E[logp(x)−logq(x)]=−p(x)a∑(logq(x)−logp(x))=p(x)a∑logq(x)p(x)
性质
DKL(p∣∣q)≥0
由Gibbs不等式:
若
∑i=1npi=∑i=1nqi=1,且
pi,qi∈(0,1],则有:
−i∑npilogpi≤−i∑npilogqi
当且仅当
pi=qi时等号成立。
DKL(p∣∣q)=DKL(q∣∣p)
参考资料
Label Distribution Learning
R语言实现46种距离算法
Kullback-Leibler Divergence Explained
KL散度(Kullback-Leibler Divergence)介绍及详细公式推导
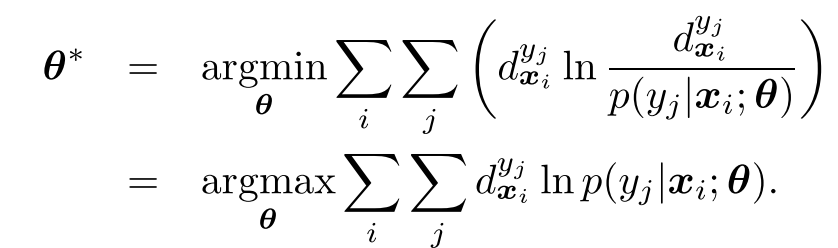
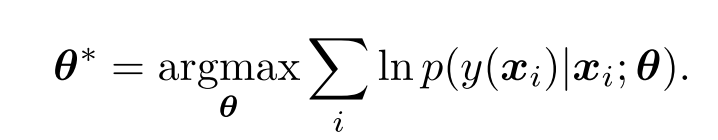
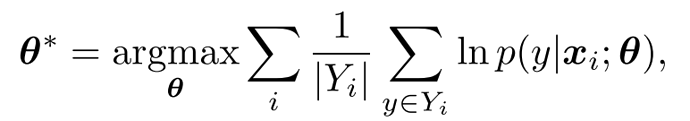



评论(0)