向量积
【摘要】
矩阵形式[编辑]
给定直角坐标系的单位向量i,j,k满足下列等式:
i ×
j =
k j ×
k =
i &n...
矩阵形式[编辑]
给定直角坐标系的单位向量i,j,k满足下列等式:
- i × j = k j × k = i k × i = j
通过这些规则,两个向量的叉积的坐标可以方便地计算出来,不需要考虑任何角度:设
- a = a 1 i + a 2 j + a 3 k = [ a 1, a 2, a 3]
- b = b 1 i + b 2 j + b 3 k = [ b 1, b 2, b 3]
则
- a × b = [a 2b 3 − a 3b 2, a 3b 1 − a 1b 3, a 1b 2 − a 2b 1]
叉积也可以用四元数来表示。注意到上述i,j,k之间的叉积满足四元数的乘法。一般而言,若将向量[a1, a2, a3]表示成四元数a1i + a2j + a3k,两个向量的叉积可以这样计算:计算两个四元数的乘积得到一个四元数,并将这个四元数的实部去掉,即为结果。更多关于四元数乘法,向量运算及其几何意义请参见四元数与空间旋转。
文章来源: blog.csdn.net,作者:fengda2870,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/fengda2870/article/details/22397173
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者

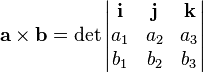

评论(0)