AEJoy —— 表达式之速度和频率控制（二）【JS】

理解产生问题的原因

学习如何解决问题的第一步是理解为什么显而易见的解决方案不起作用。问题的根源在于表达式没有记忆。在前面的示例中，表达式在每一帧检索速度控制滑块的当前值，并使用该值来计算当前旋转 —— 而不考虑滑块的以前值。如果滑块一直在它的当前值，结果(对于每一帧)是相同的。所以当滑块最终返回 0 时（例如，表达式将总旋转计算为 0），这显然不是我们想要的。我们的表达式需要计算由于滑块的所有先前值的累积旋转。然后，当滑块返回 0 时，表达式将计算旋转的总角度，而不是本身返回 0 。现在我们有了一个计划，但该怎么做呢?

线性关键帧积分器

在这种情况下，解决问题的关键涉及到一点微积分。不要惊慌，这并不难理解，而且是一个非常有用的概念。原来这个谜题中缺失的部分就是所谓的积分。利用微积分，如果你对速度与时间积分，你就能得到移动的距离(或者在这种情况下，旋转的总角度)。实际上，你可以通过计算曲线下的面积来实现，而这正是这里所需要的。“曲线下面积” 是什么意思? 本例中的 “曲线” 是 Slider Control（滑块控件）值与时间的关系图。

Slider Control 的图形会上升到每秒 360 度，保持该值 2 秒，然后下降到 0

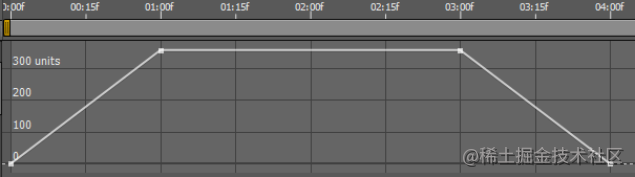
在这种情况下，要计算曲线下的面积，最简单的方法是将工作分成三个部分。这三个片段中的每一个都由线性关键帧限定。首先是三角形部分ÿ

文章来源: panda1234lee.blog.csdn.net，作者：panda1234lee，版权归原作者所有，如需转载，请联系作者。

原文链接：panda1234lee.blog.csdn.net/article/details/121529437