【小Y学算法】⚡️每日LeetCode打卡⚡️——30.平衡二叉树
【摘要】 📢前言 🚀 算法题 🚀 🌲 每天打卡一道算法题,既是一个学习过程,又是一个分享的过程😜🌲 提示:本专栏解题 编程语言一律使用 C# 和 Java 两种进行解题🌲 要保持一个每天都在学习的状态,让我们一起努力成为算法大神吧🧐!🌲 今天是力扣算法题持续打卡第30天🎈! 🚀 算法题 🚀 🌲原题样例:平衡二叉树给定一个二叉树,判断它是否是高度平衡的二叉树。本题中...

📢前言
| 🚀 算法题 🚀 |
- 🌲 每天打卡一道算法题,既是一个学习过程,又是一个分享的过程😜
- 🌲 提示:本专栏解题 编程语言一律使用 C# 和 Java 两种进行解题
- 🌲 要保持一个每天都在学习的状态,让我们一起努力成为算法大神吧🧐!
- 🌲 今天是力扣算法题持续打卡第30天🎈!
| 🚀 算法题 🚀 |
🌲原题样例:平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 1:
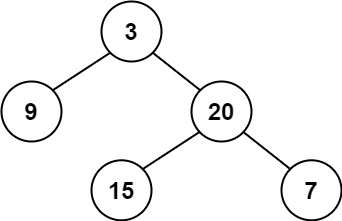
输入:root = [3,9,20,null,null,15,7]
输出:true
示例 2:
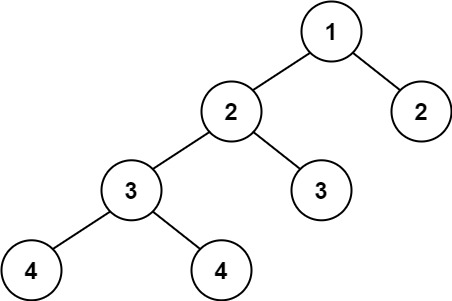
输入:root = [1,2,2,3,3,null,null,4,4]
输出:false
示例 3:
输入:root = []
输出:true
提示:
- 树中的节点数在范围 [0, 5000] 内
- -104 <= Node.val <= 104
🌻C#方法:中序遍历
这道题中的平衡二叉树的定义是:二叉树的每个节点的左右子树的高度差的绝对值不超过 11,则二叉树是平衡二叉树。
根据定义,一棵二叉树是平衡二叉树,当且仅当其所有子树也都是平衡二叉树,因此可以使用递归的方式判断二叉树是不是平衡二叉树,递归的顺序可以是自顶向下或者自底向上。
思路解析

代码:
public class Solution {
public bool IsBalanced(TreeNode root) {
if(root==null)
return true;
else
return Math.Abs(Height(root.left)-Height(root.right))<=1&&IsBalanced(root.left)&&IsBalanced(root.right);
}
public static int Height(TreeNode root){
if(root==null)
return 0;
else
return Math.Max(Height(root.left),Height(root.right))+1;
}
}
执行结果
通过
执行用时:92 ms,在所有 C# 提交中击败了73.75%的用户
内存消耗:27 MB,在所有 C# 提交中击败了94.38%的用户
复杂度分析
时间复杂度:O( n^2 ),其中 n 是数组的长度。每个数字只访问一次。
空间复杂度:O( n ),其中 n 是数组的长度。空间复杂度不考虑返回值,因此空间复杂度主要取决于递归栈的深度,递归栈的深度是O(logn)。
🌻Java 方法一:自顶向下的递归
思路解析

代码:
class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null) {
return true;
} else {
return Math.abs(height(root.left) - height(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
}
}
public int height(TreeNode root) {
if (root == null) {
return 0;
} else {
return Math.max(height(root.left), height(root.right)) + 1;
}
}
}
执行结果
通过
执行用时:1 ms,在所有 Java 提交中击败了79.28%的用户
内存消耗:38.5 MB,在所有 Java 提交中击败了34.42%的用户
复杂度分析
时间复杂度:O( n^2 ),其中 n 是数组的长度。每个数字只访问一次。
空间复杂度:O( n ),其中 n 是数组的长度。空间复杂度不考虑返回值,因此空间复杂度主要取决于递归栈的深度,递归栈的深度是O(logn)。
🌻Java 方法二:自底向上的递归
思路解析
方法一由于是自顶向下递归,因此对于同一个节点,函数 height 会被重复调用,导致时间复杂度较高。
如果使用自底向上的做法,则对于每个节点,函数 height 只会被调用一次。
自底向上递归的做法类似于后序遍历,对于当前遍历到的节点,先递归地判断其左右子树是否平衡,再判断以当前节点为根的子树是否平衡。
如果一棵子树是平衡的,则返回其高度(高度一定是非负整数),否则返回 -1−1。
如果存在一棵子树不平衡,则整个二叉树一定不平衡。
代码:
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int p1 = 0, p2 = 0;
int[] sorted = new int[m + n];
int cur;
while (p1 < m || p2 < n) {
if (p1 == m) {
cur = nums2[p2++];
} else if (p2 == n) {
cur = nums1[p1++];
} else if (nums1[p1] < nums2[p2]) {
cur = nums1[p1++];
} else {
cur = nums2[p2++];
}
sorted[p1 + p2 - 1] = cur;
}
for (int i = 0; i != m + n; ++i) {
nums1[i] = sorted[i];
}
}
}
执行结果
通过
执行用时:1 ms,在所有 Java 提交中击败了79.28%的用户
内存消耗:38.1 MB,在所有 Java 提交中击败了96.98%的用户
复杂度分析
时间复杂度:O(n)
空间复杂度:O(n)
💬总结
- 今天是力扣算法题打卡的第三十天!
- 文章采用
C#和Java两种编程语言进行解题 - 一些方法也是参考力扣大神写的,也是边学习边分享,再次感谢算法大佬们
- 那今天的算法题分享到此结束啦,明天再见!

【版权声明】本文为华为云社区用户原创内容,转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息, 否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者



评论(0)