《重学数据结构》之什么是二叉树?
【摘要】
基本概念
树,一种非线性表数据结构:
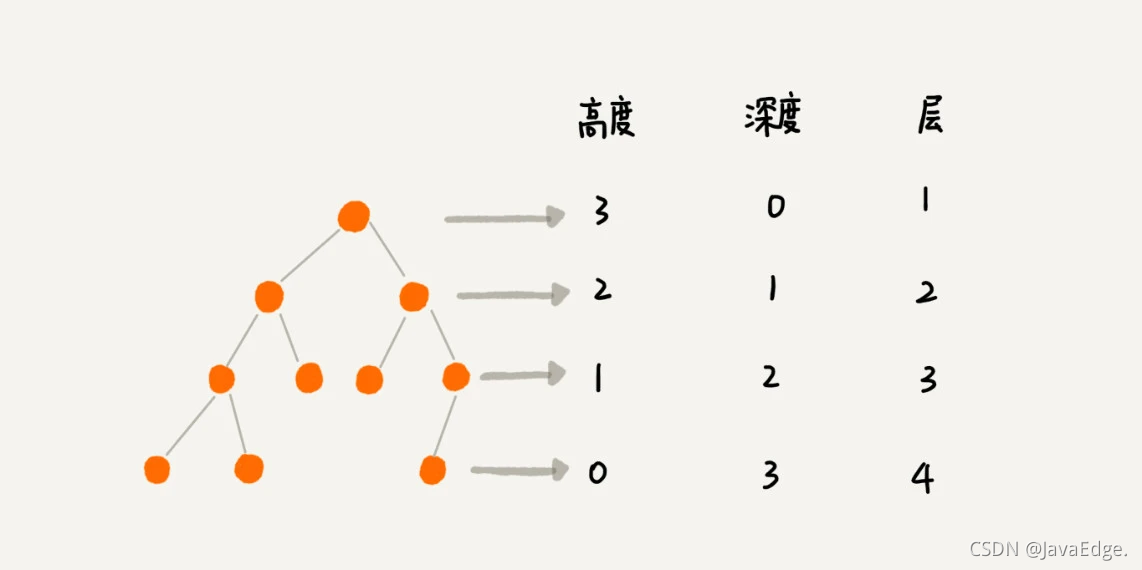
节点 “树”里面的每个元素父子关系 连线相邻节点之间的关系兄弟节点 节点的父节点是同一个节点根节点 没有父节点的节点叶(子)节点 没有子节点的节点节点的高度 节点...
基本概念
树,一种非线性表数据结构:
- 节点
“树”里面的每个元素 - 父子关系
连线相邻节点之间的关系 - 兄弟节点
节点的父节点是同一个节点 - 根节点
没有父节点的节点 - 叶(子)节点
没有子节点的节点 - 节点的高度
节点到叶节点的最长路径(边数) - 树的高度
根节点的高度 - 节点的深度
根节点到该节点所经历的边的个数 - 节点的层数
节点的深度+1

二叉树(Binary Tree)
最常用的树结构。
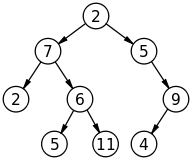
每个节点最多有两个子节点:左子节点,右子节点。
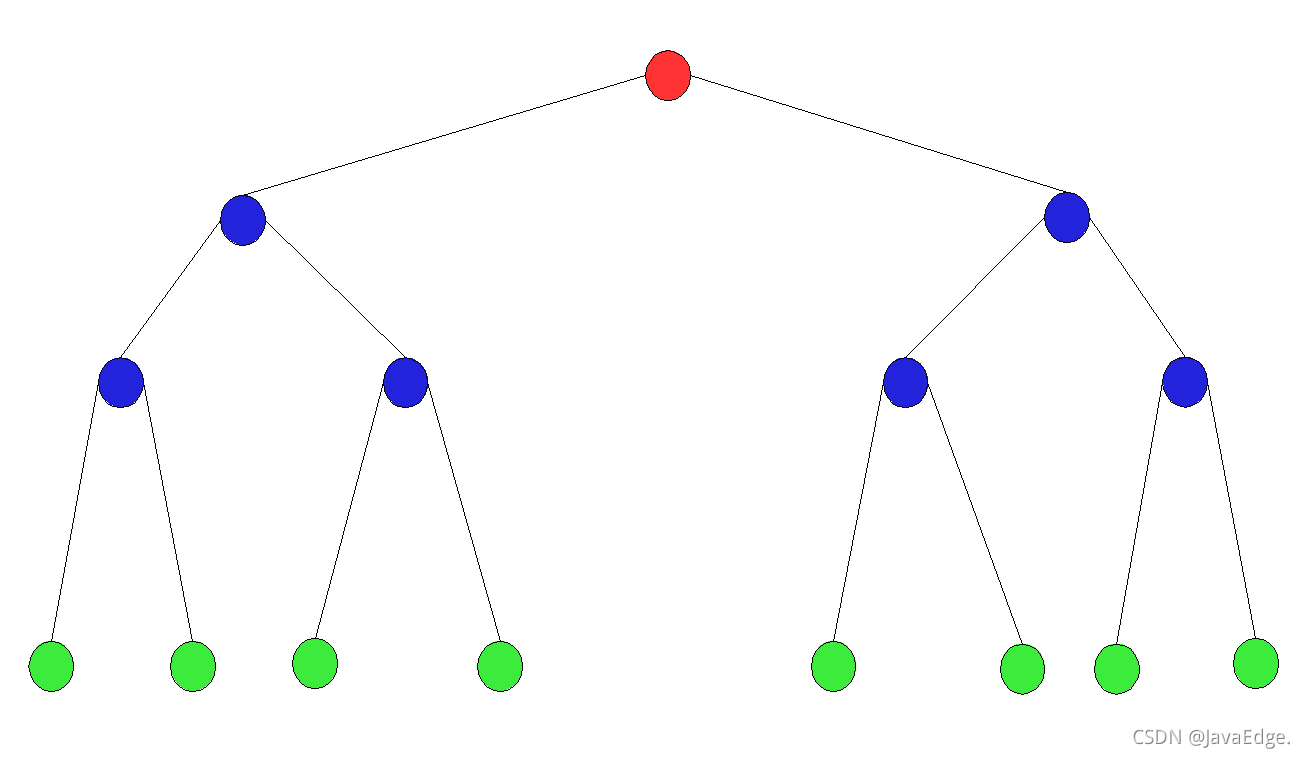
- 满二叉树
叶节点全在最底层,除叶节点外,每个节点都有左右两个子节点

- 完全二叉树
叶节点都在最底下两层,最后一层的叶节点都靠左排列,且除最后一层,其他层节点个数都达到最大
为啥就把最后一层的叶子节点靠左排列的叫完全二叉树?靠右排列为啥就不行?
要搞清楚完全二叉树为啥这么定义,先学习
如何存储二叉树?
基于指针或者引用的二叉链式存储法
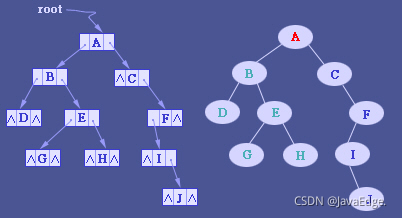
每个节点有三个字段:
- 一个存储数据
- 另两个指向左右子节点的指针
大部分二叉树代码都是通过这种结构实现的。
基于数组的顺序存储法
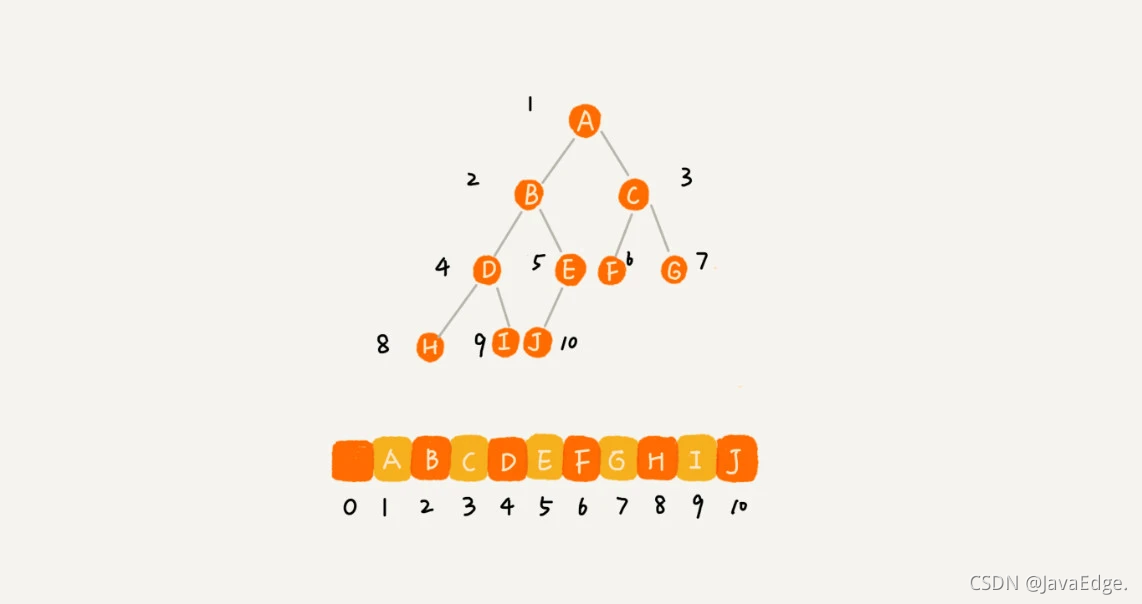
若节点X存储在数组中下标为i的位置
2 * i 存储左子节点
2 * i + 1存储右子节点
i/2存储其父节点
由于这是个完全二叉树,所以仅“浪费”了一个下标0的存储位置。若是非完全二叉树,就会浪费较多存储空间:
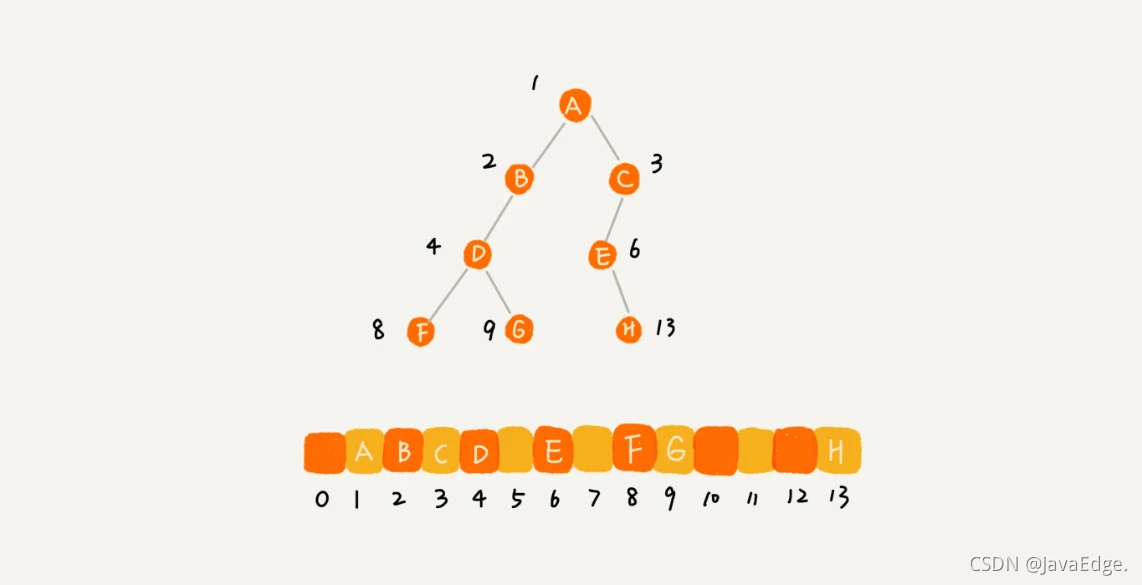
所以完全二叉树用数组存储最省内存,就不像链式存储法,还要存储左、右子节点的指针。所以完全二叉树要求最后一层的子节点都靠左。
堆也是一种完全二叉树,所以其最常用的存储方式就是数组。
二叉树的遍历
经典遍历
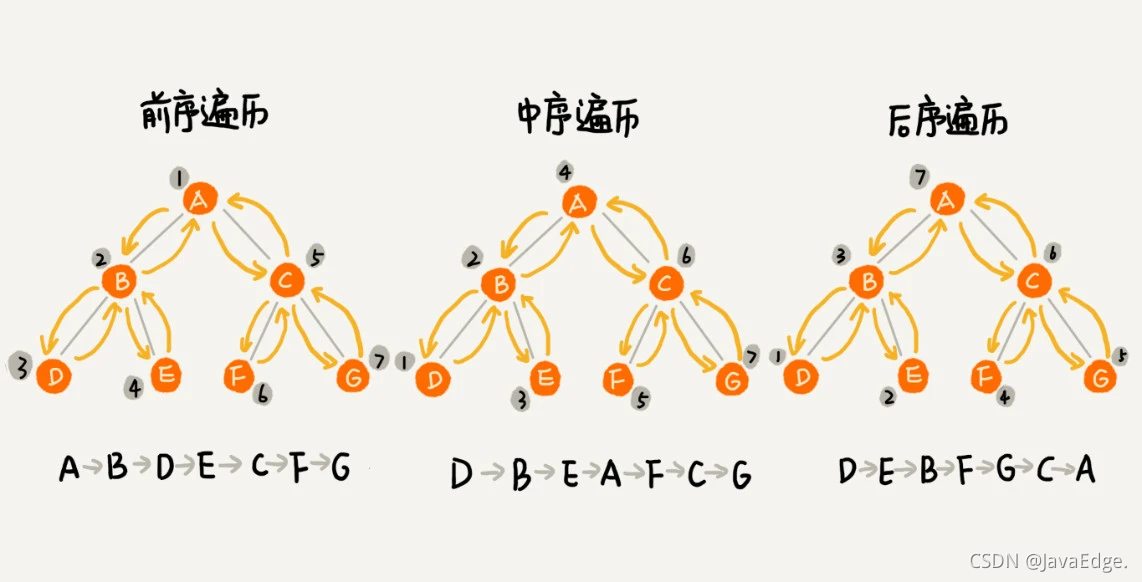
- 前序遍历
对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。 - 中序遍历
对于树中的任意节点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树。 - 后序遍历
对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身。

这些都是递归过程。
递归代码的关键就是递推公式,递推公式的关键就是,如果要解决问题A,就假设子问题B、C已经解决,然后再来看如何利用B、C来解决A。
所以可以写出前、中、后序遍历的
递推公式
前序遍历
preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)
- 1
中序遍历
inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)
- 1
后序遍历
postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r
- 1
void preOrder(Node* root) {
if (root == null) return;
print root // 此处为伪代码,表示打印root节点
preOrder(root->left);
preOrder(root->right);
}
void inOrder(Node* root) {
if (root == null) return;
inOrder(root->left);
print root // 此处为伪代码,表示打印root节点
inOrder(root->right);
}
void postOrder(Node* root) {
if (root == null) return;
postOrder(root->left);
postOrder(root->right);
print root // 此处为伪代码,表示打印root节点
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
时间复杂度
每个节点最多会被访问两次,所以遍历操作的时间复杂度,跟节点的个数n成正比,也就是说二叉树遍历的时间复杂度是O(n)。
参考
- https://zh.wikipedia.org/wiki/%E4%BA%8C%E5%8F%89%E6%A0%91
文章来源: javaedge.blog.csdn.net,作者:JavaEdge.,版权归原作者所有,如需转载,请联系作者。
原文链接:javaedge.blog.csdn.net/article/details/120121453
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)