【小Y学算法】⚡️每日LeetCode打卡⚡️——21.x 的平方根

📢前言

• 🌲 每天打卡一道算法题，既是一个学习过程，又是一个分享的过程😜
• 🌲 提示：本专栏解题 编程语言一律使用 C# 和 Java 两种进行解题
• 🌲 要保持一个每天都在学习的状态，让我们一起努力成为算法大神吧🧐！
• 🌲 今天是力扣算法题持续打卡第21天🎈！

🌲原题样例

实现int sqrt(int x)函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:

输入: 4
输出: 2

示例 2:
输入: 8
输出: 2
说明: 8 的平方根是 2.82842..., 
     由于返回类型是整数，小数部分将被舍去。

🌻C#方法：二分查找

思路解析

根据题意我们知道，最终目的就是返回 x 的平方根

我们可以直接调用Sqrt方法找到平方根，但是这就不是算法的本意啦~

所以可以使用二分法来解决这个问题

二分查找的下界为 0，上界可以粗略地设定为 x。

在二分查找的每一步中，我们只需要比较中间元素 mid 的平方与 x 的大小关系，并通过比较的结果调整上下界的范围。
由于我们所有的运算都是整数运算，不会存在误差

用 mid==x/mid 而不是 mid*mid==x 防止数值溢出

代码：

public class Solution {
 
      public  int MySqrt(int x)
        {
            if (x == 0) return 0;
            int left = 1, right = x, mid = (left+right)/2;
            while(left<right&&mid!=left)
            {
                if(mid== x/mid)
                {
                    return mid;
                }else if(mid < x / mid)
                {
                    left = mid;
                    mid = (left + right) / 2;
                }
                else
                {
                    right = mid;
                    mid = (left + right) / 2;
                }
            }
                return left;
        }
}

执行结果

通过
执行用时：44 ms，在所有 C# 提交中击败了57.74%的用户
内存消耗：14.7 MB，在所有 C# 提交中击败了1000.00%的用户

复杂度分析

时间复杂度：O( long x)
空间复杂度：O(1)

🌻Java 方法一：二分法

思路解析

由于 x 平方根的整数部分 ans 是满足 k^2 ≤x 的最大 k 值，因此我们可以对 k 进行二分查找，从而得到答案。

二分查找的下界为 0，上界可以粗略地设定为 x。
在二分查找的每一步中，我们只需要比较中间元素mid 的平方与 x 的大小关系，并通过比较的结果调整上下界的范围。

由于我们所有的运算都是整数运算，不会存在误差，因此在得到最终的答案 ans 后，也就不需要再去尝试ans+1 了。

代码：

class Solution {
    public int mySqrt(int x) {
        int l = 0, r = x, ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long) mid * mid <= x) {
                ans = mid;
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return ans;
    }
}

执行结果

通过
执行用时：1 ms，在所有 Java  提交中击败了100.00%的用户
内存消耗：35.3 MB，在所有 Java 提交中击败了92.27%的用户

复杂度分析

时间复杂度：O( long x)
空间复杂度：O(1)

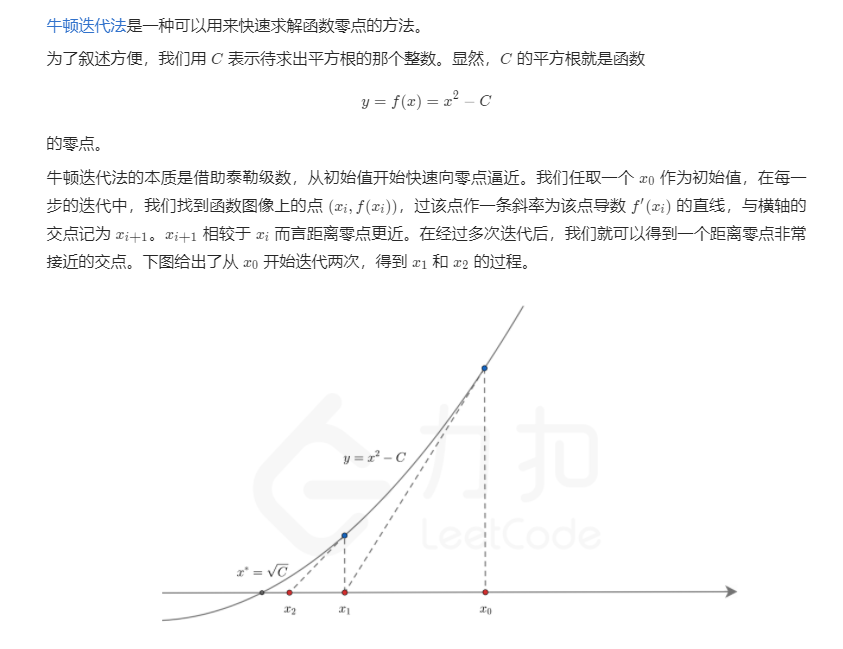
🌻Java 方法二：牛顿迭代

思路解析

这个方法是力扣官方解答，放在这给大家看看即可，我并没有看得很明白。。。

class Solution {
    public int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }

        double C = x, x0 = x;
        while (true) {
            double xi = 0.5 * (x0 + C / x0);
            if (Math.abs(x0 - xi) < 1e-7) {
                break;
            }
            x0 = xi;
        }
        return (int) x0;
    }
}

执行结果

通过
执行用时：1 ms，在所有 Java  提交中击败了100.00%的用户
内存消耗：35.5 MB，在所有 Java 提交中击败了57.42%的用户

复杂度分析

时间复杂度：O( long x)
空间复杂度：O(1)

💬总结

• 今天是力扣算法题打卡的第二十一天！
• 文章采用 C#和 Java 两种编程语言进行解题
• 一些方法也是参考力扣大神写的，也是边学习边分享，再次感谢算法大佬们
• 那今天的算法题分享到此结束啦，明天再见！
  

🚀往期优质文章分享

• ❤️Unity零基础到入门 | 游戏引擎 Unity 从0到1的 系统学习 路线【全面总结-建议收藏】！
• 🧡花一天时间做一个高质量飞机大战游戏，过万字Unity完整教程！漂亮学妹看了直呼666！
• 💛回忆童年和小伙伴一起玩过的经典游戏【炸弹人小游戏】制作过程+解析
• 💚通宵一晚做出来的一款类似CS的第一人称射击游戏Demo！原来做游戏也不是很难
• 🤍爆肝整整一个周末写一款类似 皇室战争 的 即时战斗类 游戏Demo！两万多字游戏制作过程+解析！
• 💙一款类似“恐龙快打”的 横版街机格斗游戏 该如何制作？| 一起来学习 顺便送源码【码文不易，建议收藏学习】
• 💜【超实用技巧】| 提高写文的质量 和 速率必学技能： Typora 图床配置 详细说明