[课程复习] 数据结构之线性表、树、图、查找、排序经典算法复习
作者最近在复习考博,乘此机会分享一些计算机科学与技术、软件工程等相关专业课程考题,一方面分享给考研、考博、找工作的博友,另一方面也是自己今后完成这些课程的复习资料,同时也是在线笔记。基础知识,希望对您有所帮助,不喜勿喷~
无知•乐观•低调•谦逊•生活
无知的我需要乐观的去求知,低调的底色是谦逊,而谦逊是源于对生活的通透,我们不止有工作、学习、编程,还要学会享受生活,人生何必走得这么匆忙!成都倒计时,加油,补充几张好看的框架图给大家。书阁觅知音,浔声只倾心。

文章目录
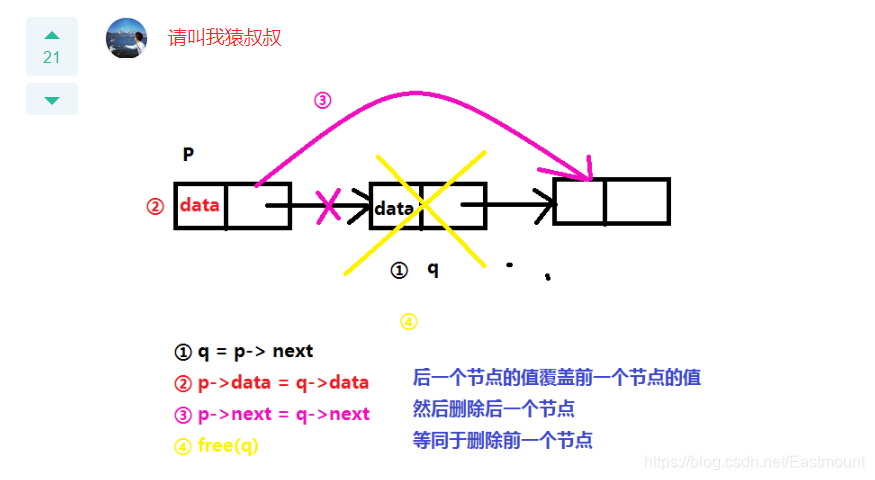
示例1:删除但列表中的相同节点元素。

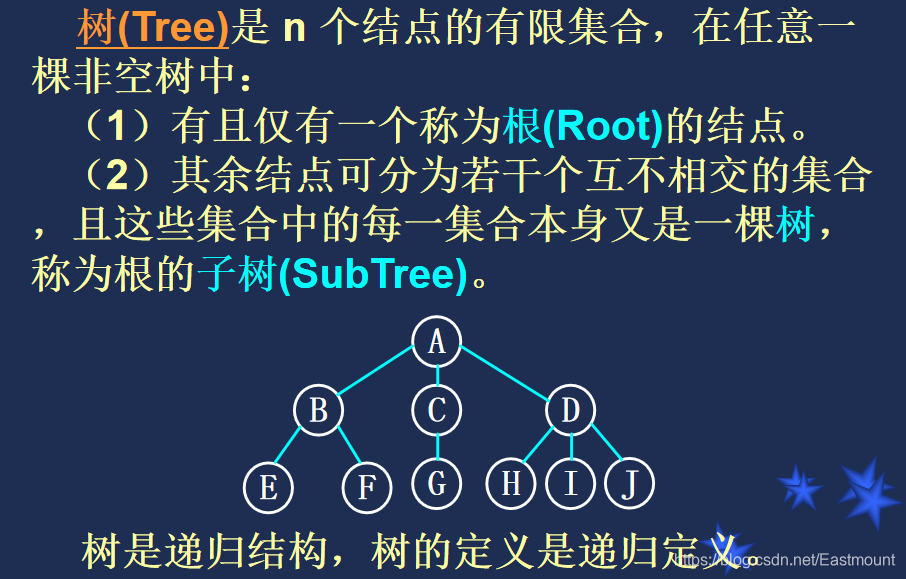

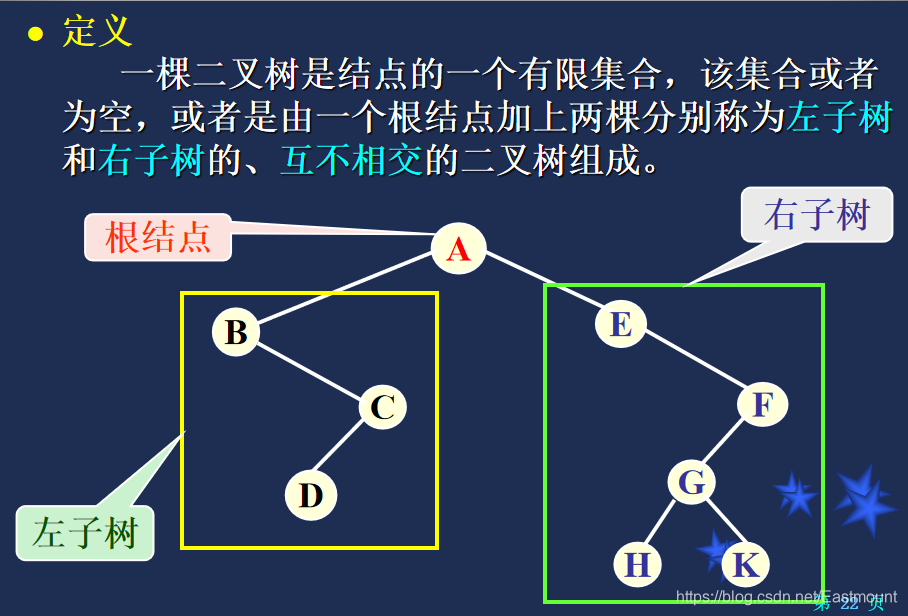
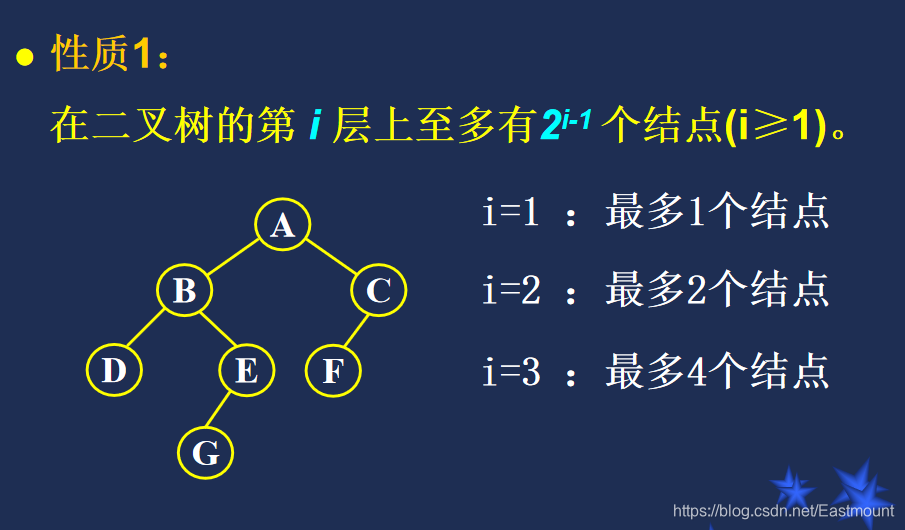





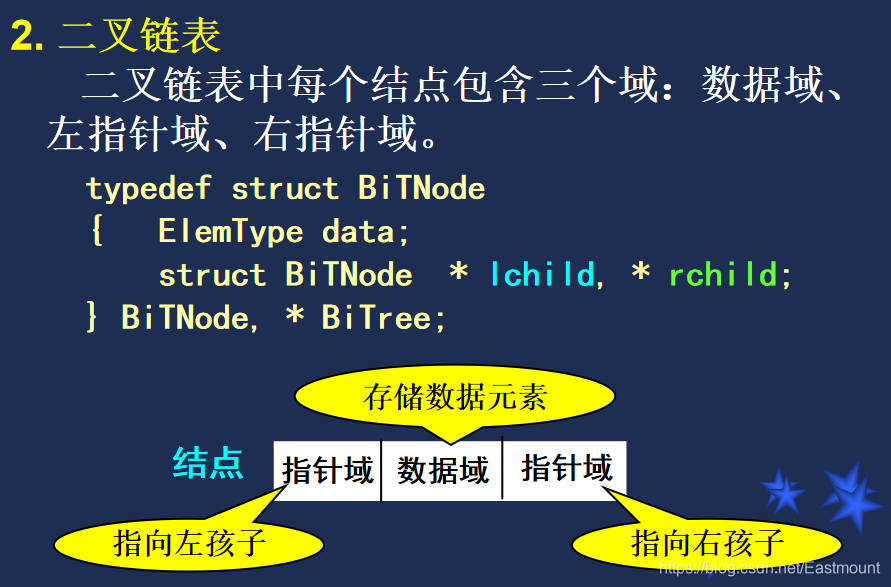
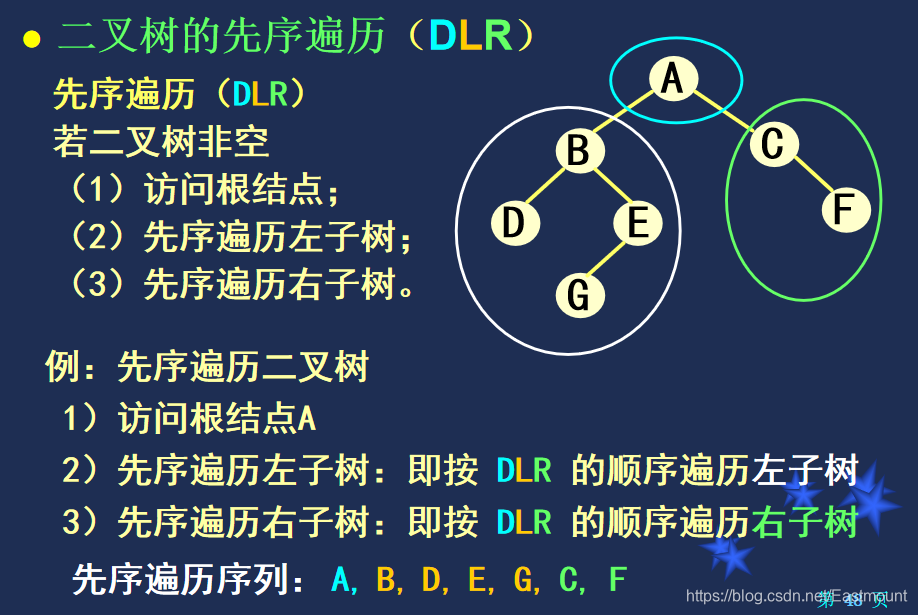
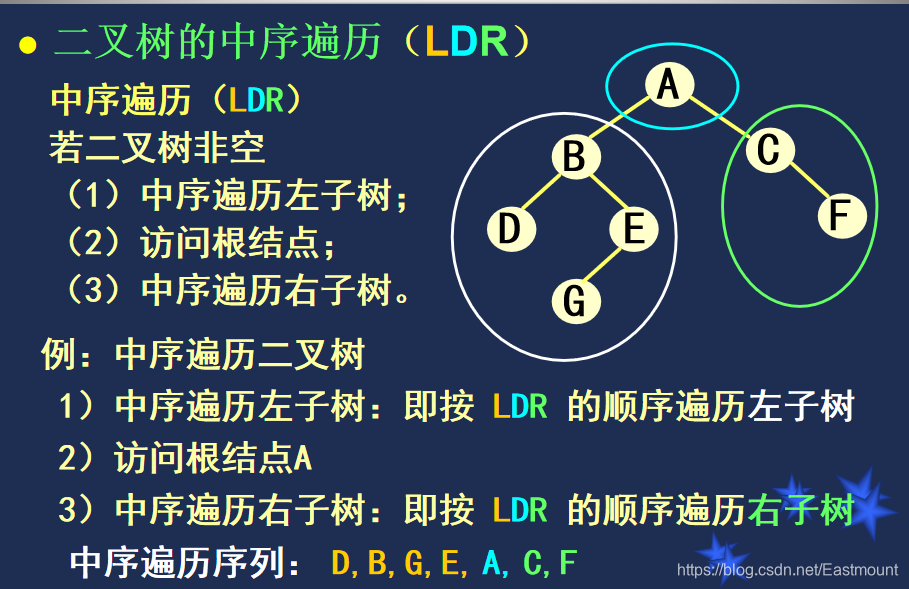
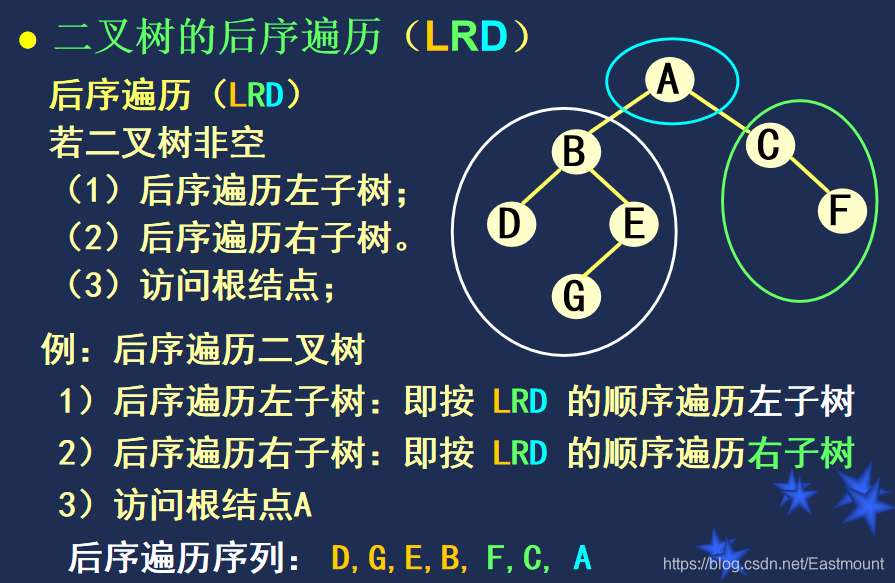
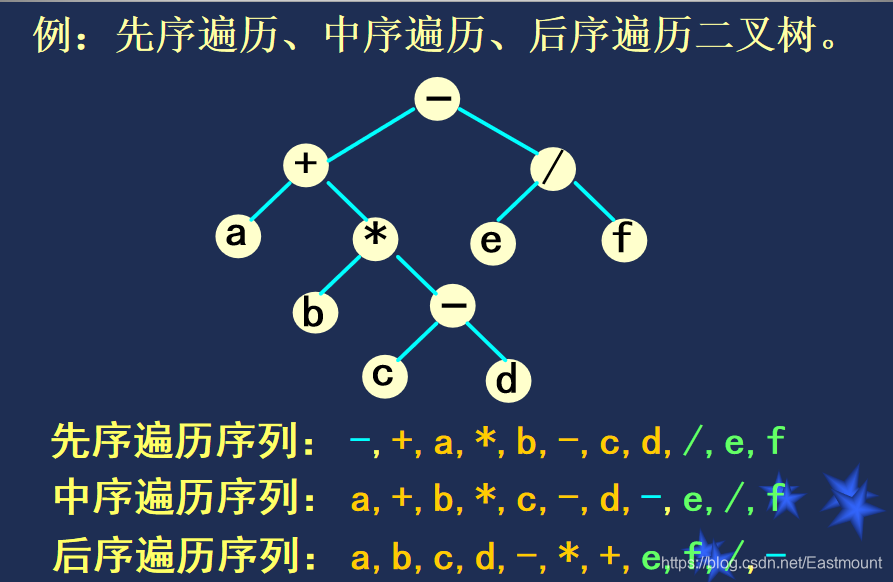
举例:
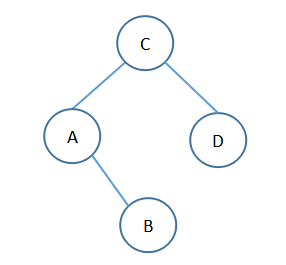
设某棵二叉树的中序遍历序列为ABCD,前序遍历序列为CABD,则后序遍历该二叉树得到序列为( )。
解析:
通过中序遍历和前序遍历可以将树构建出来,再求其后序遍历结果。
前序遍历(先根排序),故C为根节点,再看中序遍历可知,AB为C的左子树,D为其右子树。AB - C - D
前序遍历第二个节点为A,则A为根节点,再看中序遍历B在A后面,则B为右子树,最终构建树如下图所示。
答案:后序遍历结果为 BADC。
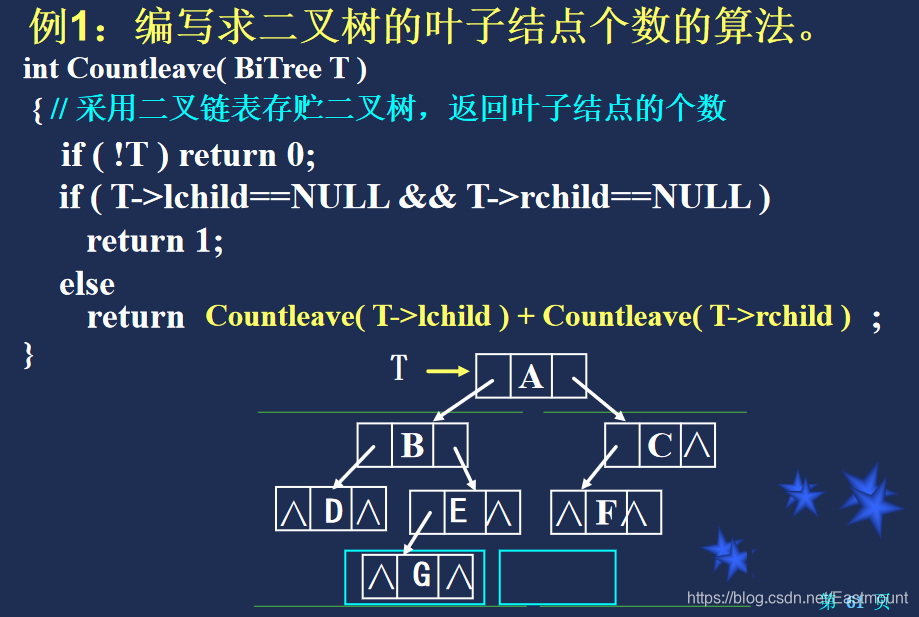
代码:


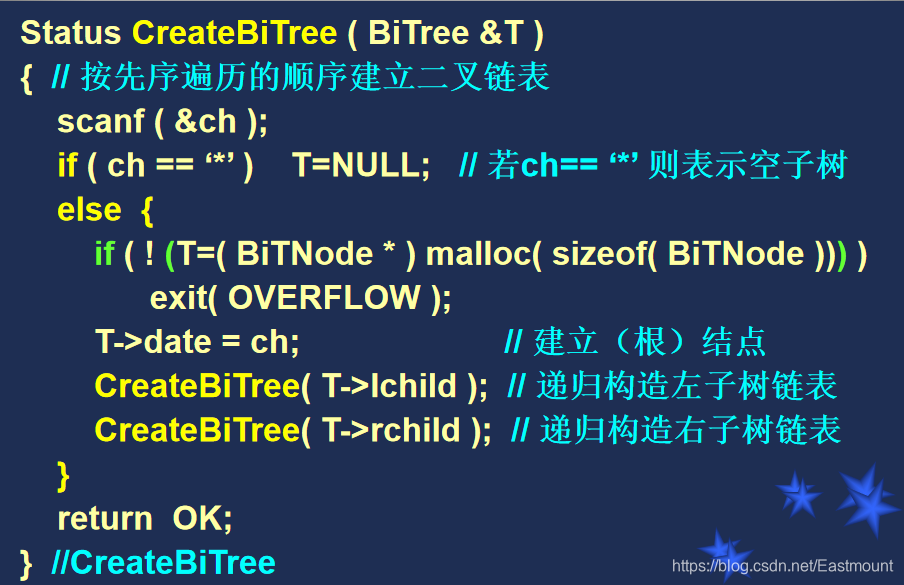
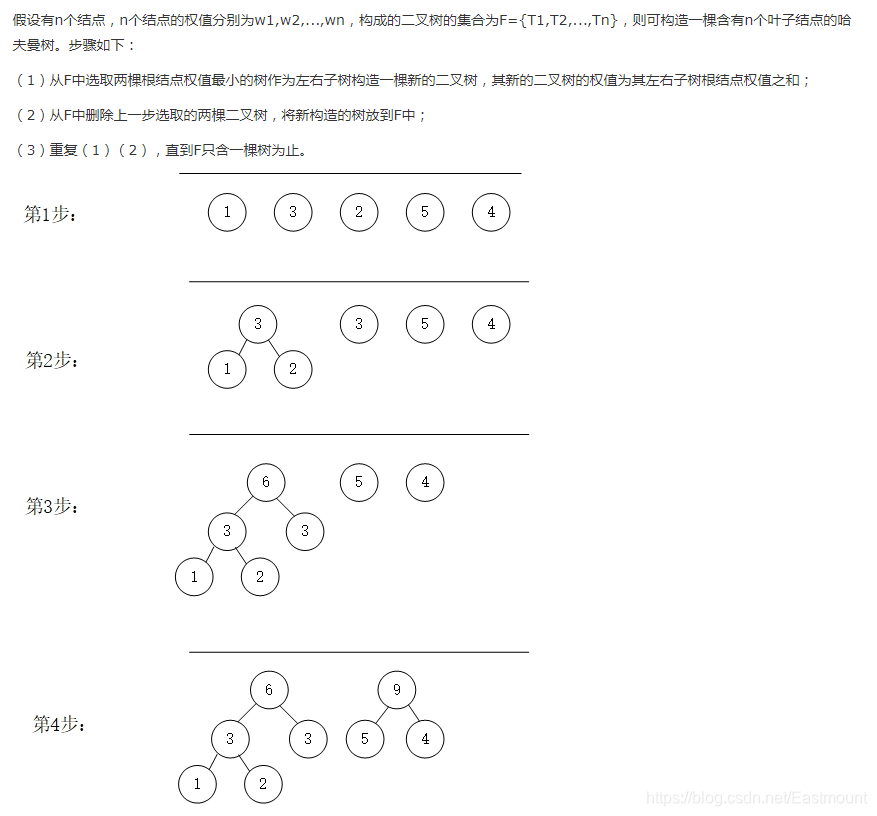
举例:
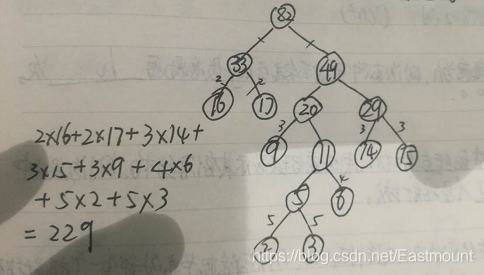
设一组权值集合W=(15,3,14,2,6,9,16,17),要求根据这些权值集合构造一棵哈夫曼树,则这棵哈夫曼树的带权路径长度为( )。


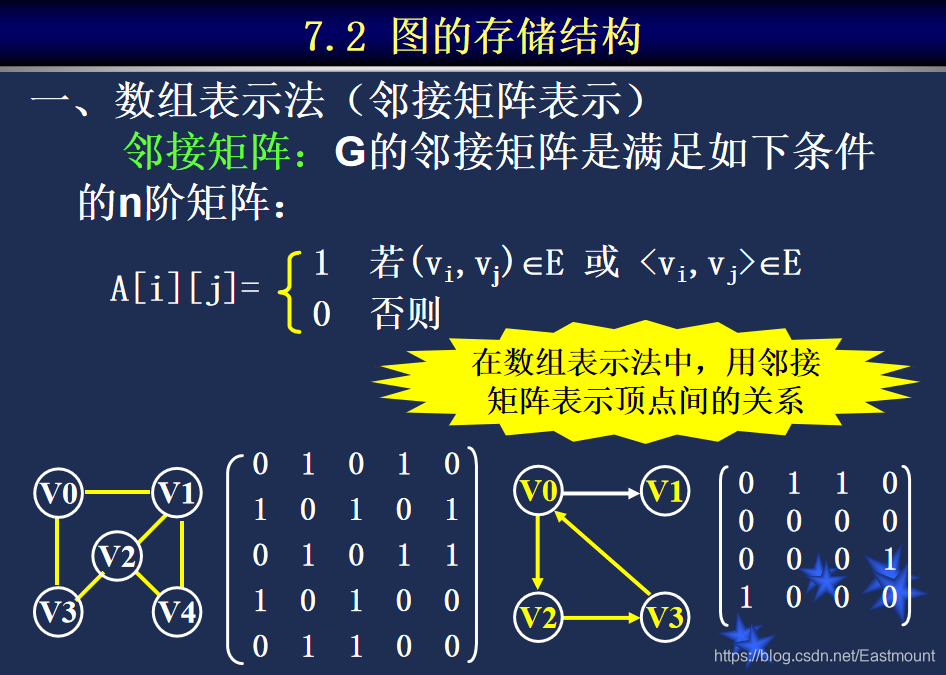
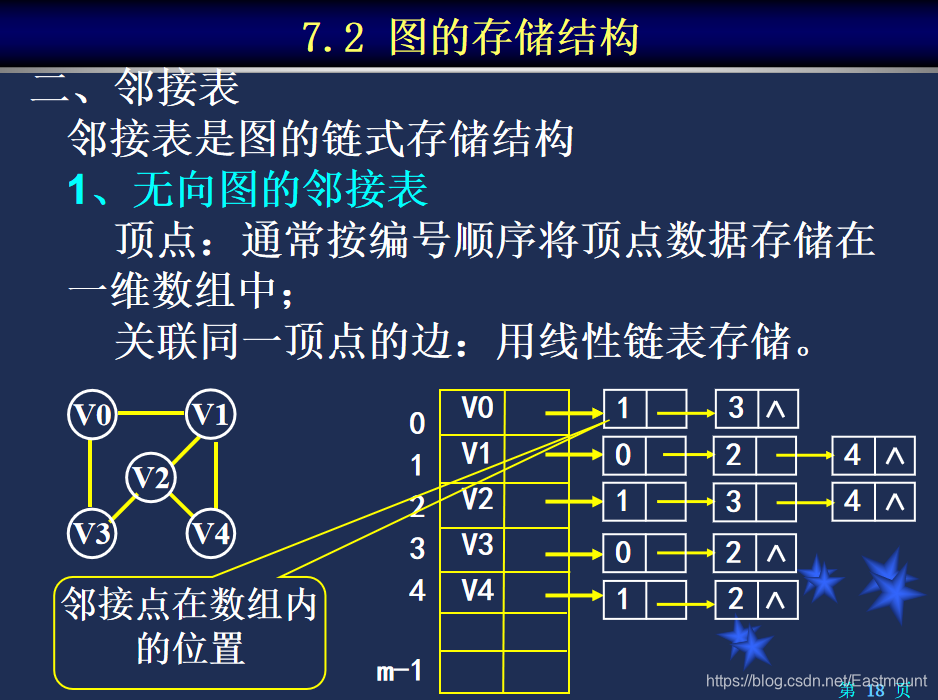
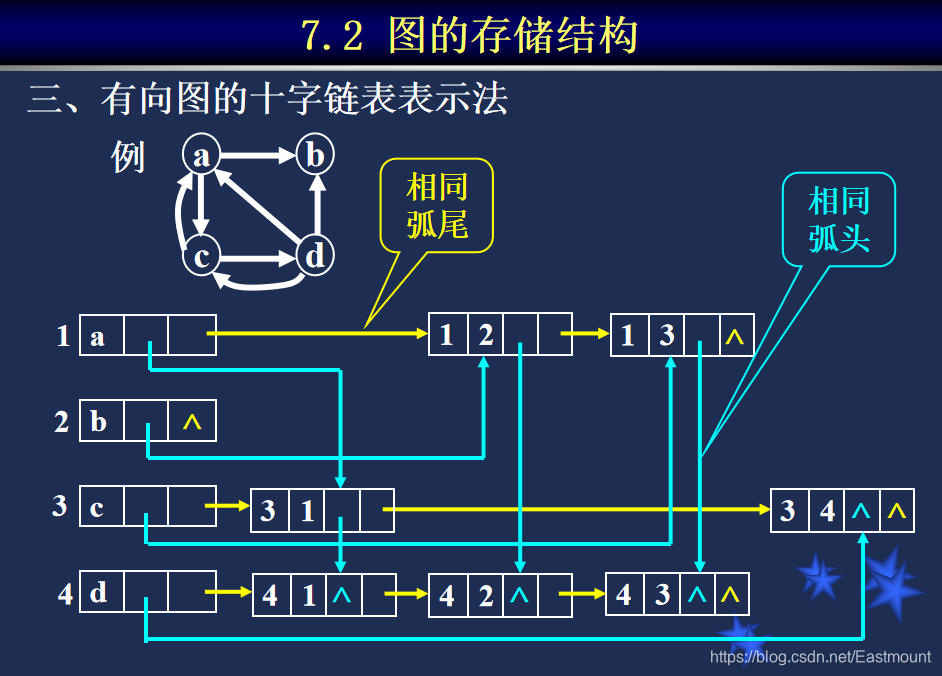
DFS:深度优先搜索

DFS代码:
// DFS的递归实现
void DFS_Recursive(Node* pRoot)
{
if (pRoot==NULL)
return;
cout<<pRoot->nVal<<" ";
if (pRoot->pLeft!=NULL)
DFS_Recursive(pRoot->pLeft);
if (pRoot->pRight!=NULL)
DFS_Recursive(pRoot->pRight);
}
BFS:广度优先搜索
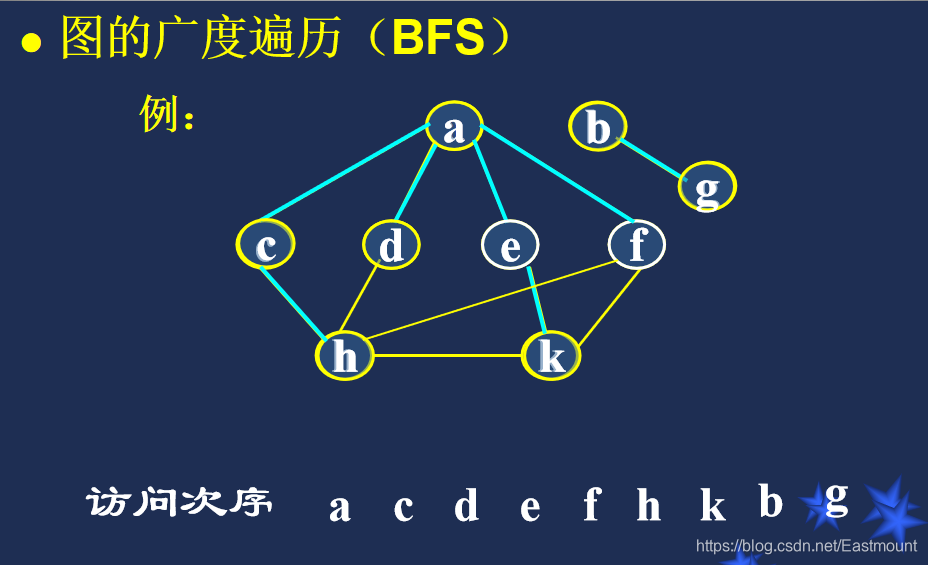
举例:
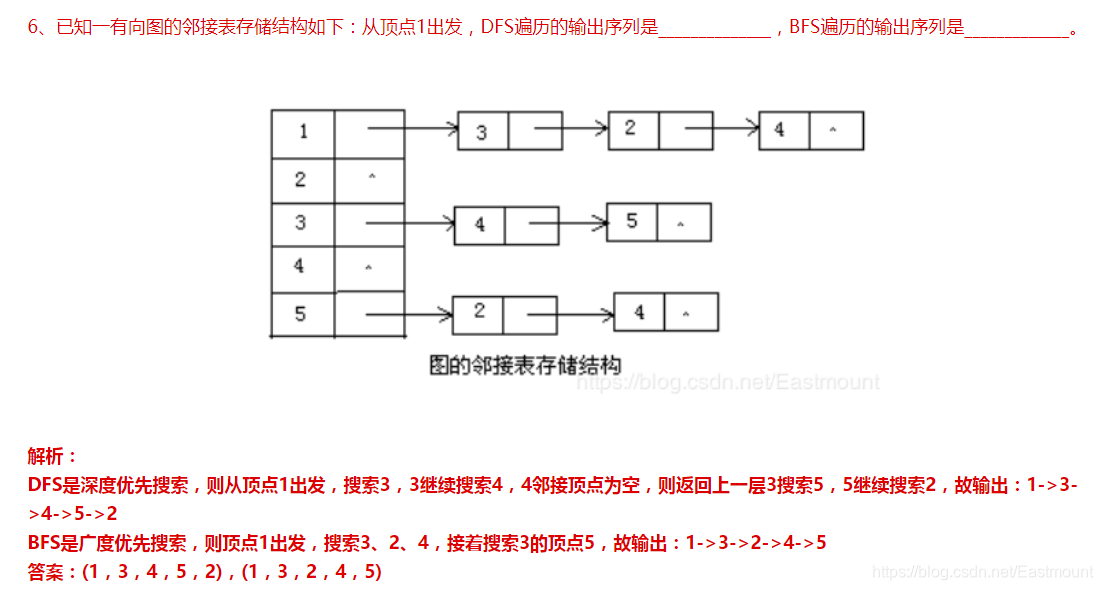
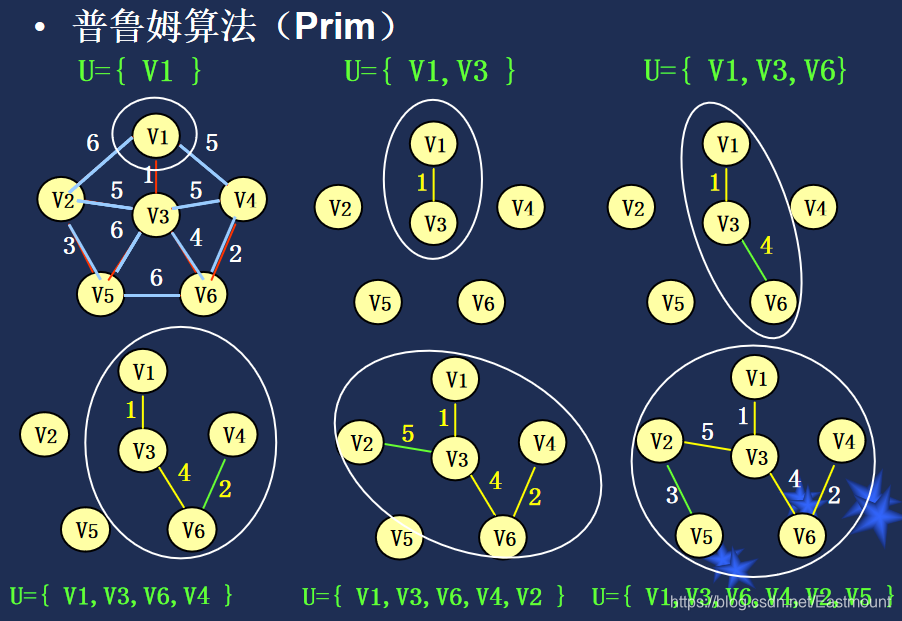
Prim算法

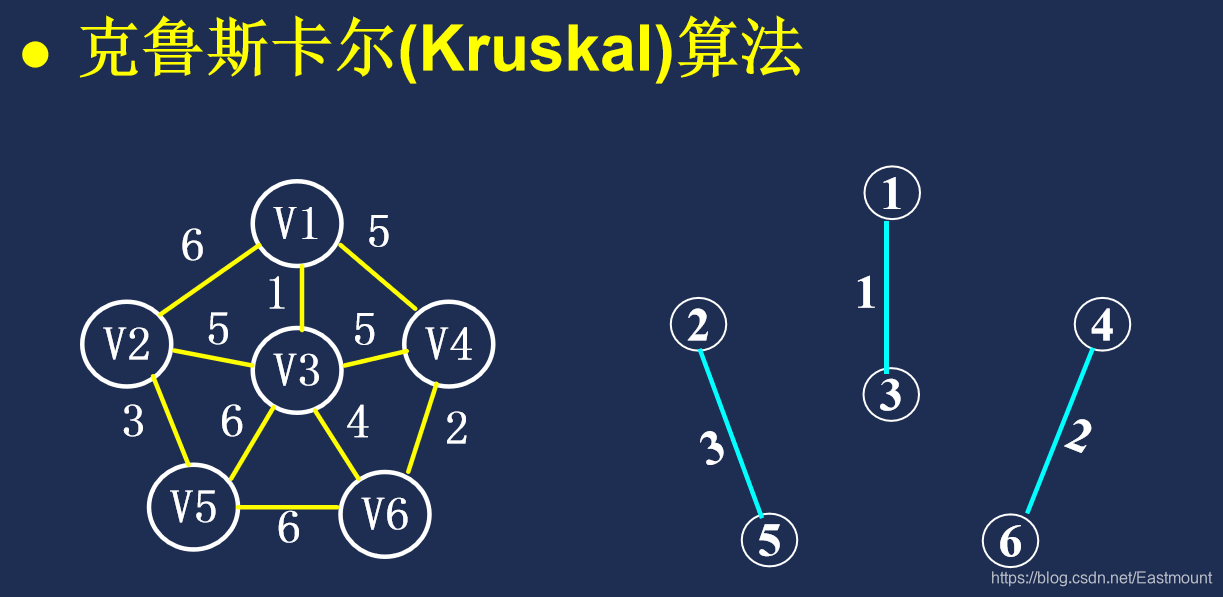
克鲁斯卡尔(Kruskal)算法
设连通网 N = ( V, {E} )。
- 初始时最小生成树只包含图的n个顶点,每个顶点为一棵子树;
- 选取权值较小且所关联的两个顶点不在同一子树的边,将此边加入到最小生成树中;
- 重复2)n-1次,即得到包含n个顶点和n-1条边的最小生成树。

拓扑排序:把AOV网络中所有顶点按照它们相互之间的优先关系排列成一个线性序列的过程。
拓扑排序的应用:是检测AOV网中是否存在环的有效方法。


Dijkstra算法
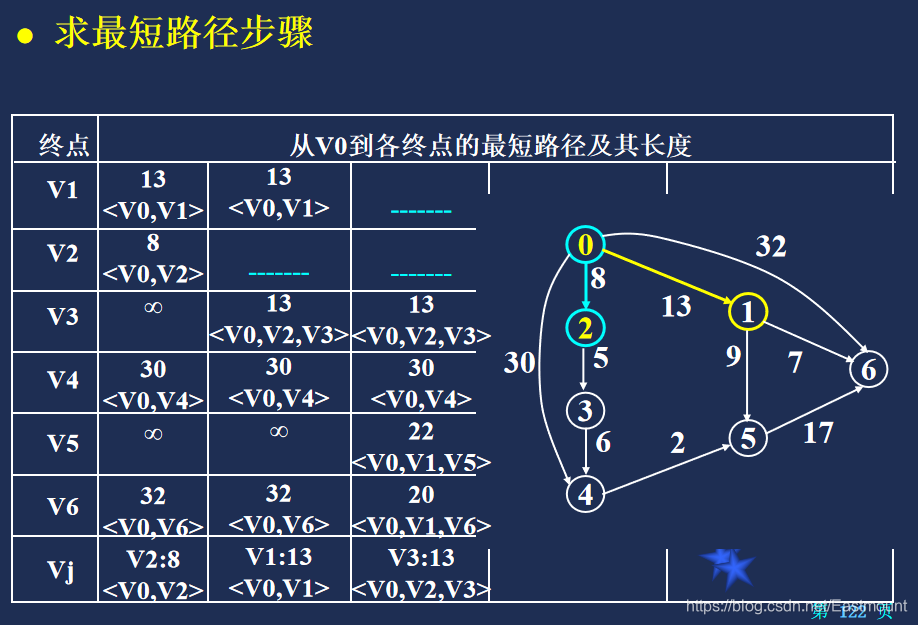

Floyd算法

如下图所示,表示折半查找的过程:

对应的代码如下所示:(背)
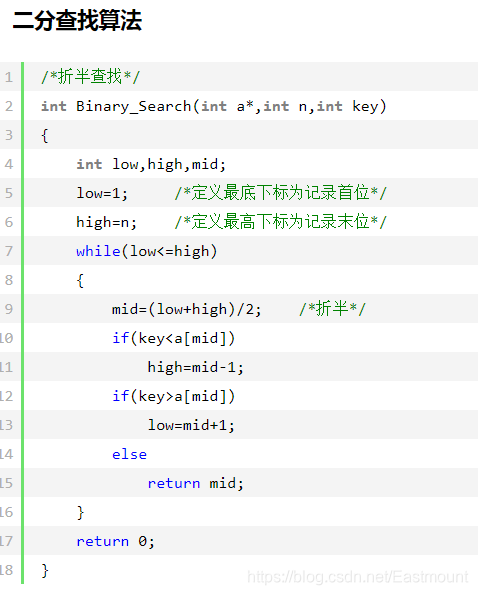
举例:
设一组有序的记录关键字序列为(13,18,24,35,47,50,62,83,90),查找方法用二分查找,要求计算出查找关键字62时的比较次数并计算出查找成功时的平均查找长度。
解析:其计算过程如下图所示。
答案:2,ASL = (1 * 1 + 2 * 2 + 3 * 4 + 4 * 2) / 9 = 25/9。

索引顺序表的查找:
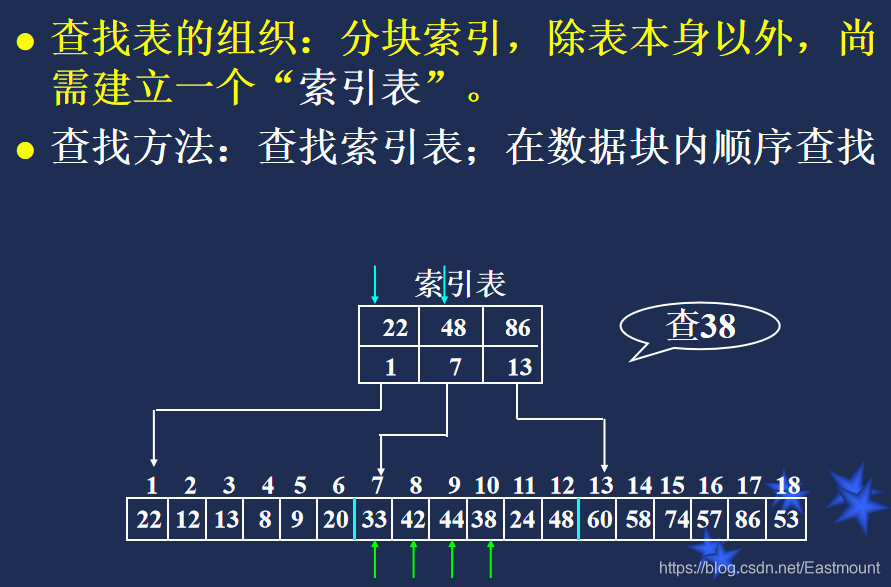
二叉排序树
二叉排序树是一棵空树,或者是具有下列性质的二叉树:
(1) 若左子树不空,则左子树上所有结点的值均小于根结点的值;
(2) 若右子树不空,则右子树上所有结点的值均大于根结点的值;
(3) 根结点的左、右子树也分别为二叉排序树。

二叉排序树的删除操作:

举例:
设一组初始记录关键字序列为 (20 , 12 , 42 , 31 , 18 , 14 , 28) ,则根据这些记录关键字构造的二叉排序树的平均查找长度是_________。
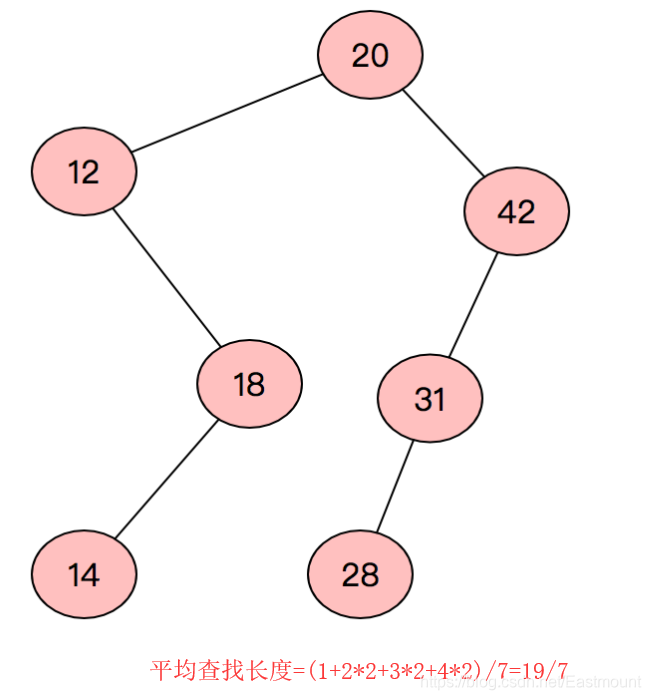
平衡二叉树


常用的解决冲突的方法:
(1) 开放地址法(线性探测再散列、二次探测再散列、随机探测再散列);
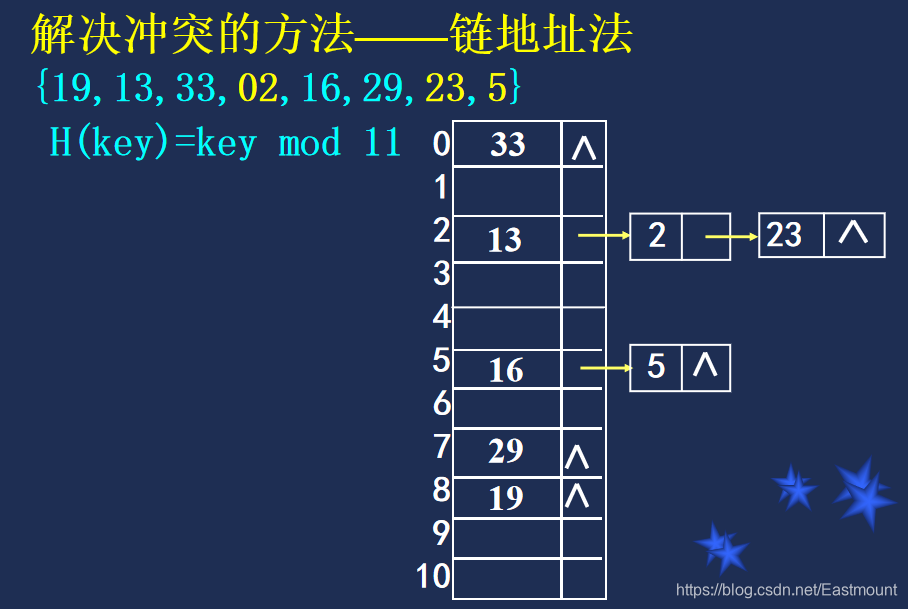
(2) 链地址法;
(3) 再哈希法;
(4) 建立一个公共溢出区。
举例:
设散列表的长度为8,散列函数H(k)=k % 7,用线性探测法解决冲突,则根据一组初始关键字序列(8,15,16,22,30,32)构造出的散列表的平均查找长度是________。
余数:0 1 2 3 4 5 6 7
8:8%7=1,1次
15:15%7=1,冲突+1,2次
16:16%7=2,与15冲突,2次
22:22%7=1,冲突3次,4次
30:30%7=2,冲突3次,4次
32:32%7=4,冲突2次,3次
故:(1 + 2 + 2 + 4 + 4 + 3)/6 = 8/3
举例:
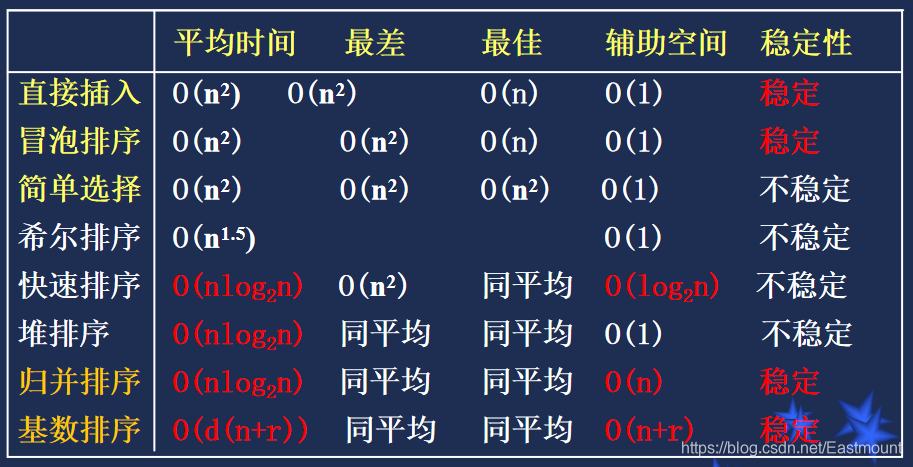
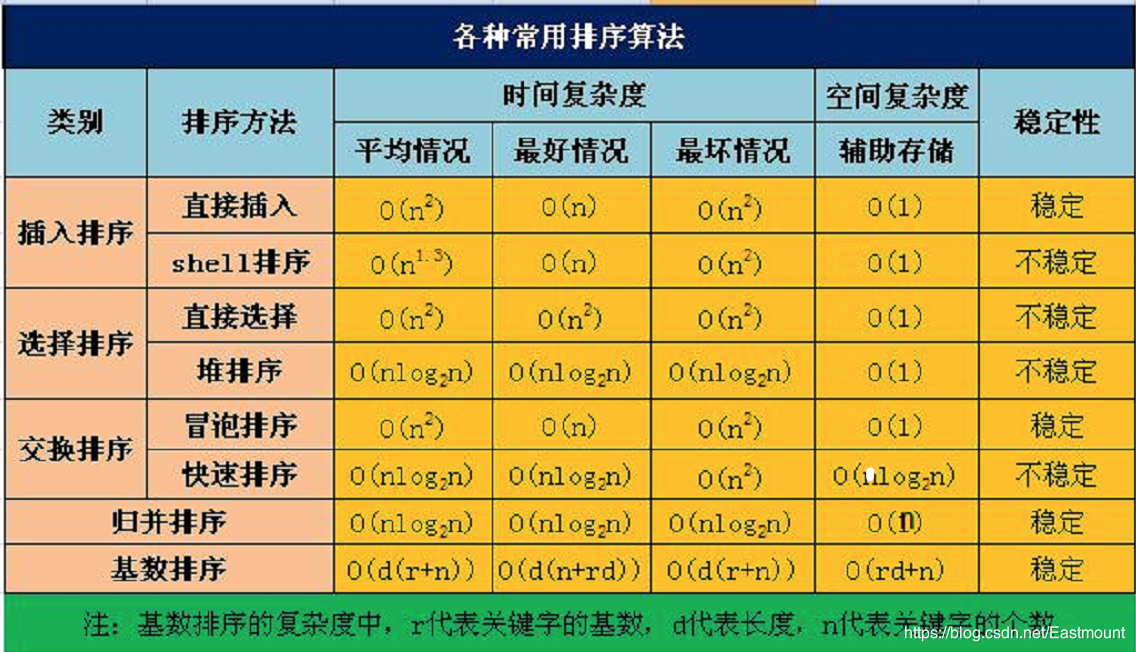
在快速排序、堆排序、归并排序中, 归并 排序是稳定的。
解析:
稳定排序:直接插入排序、冒泡排序、归并排序、基数排序
不稳定排序:希尔排序、直接选择排序、堆排序、快速排序

核心思想:两端向中间比较,并交换顺序

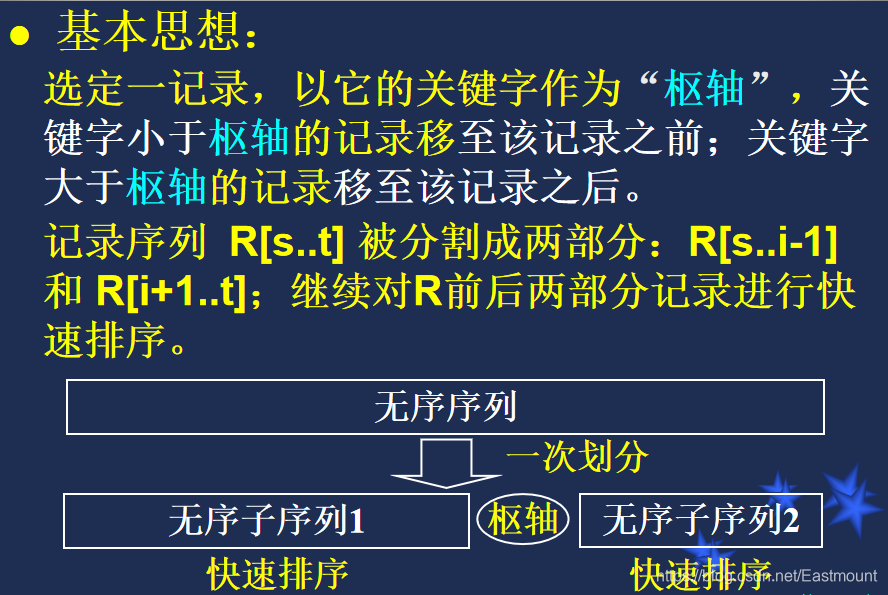
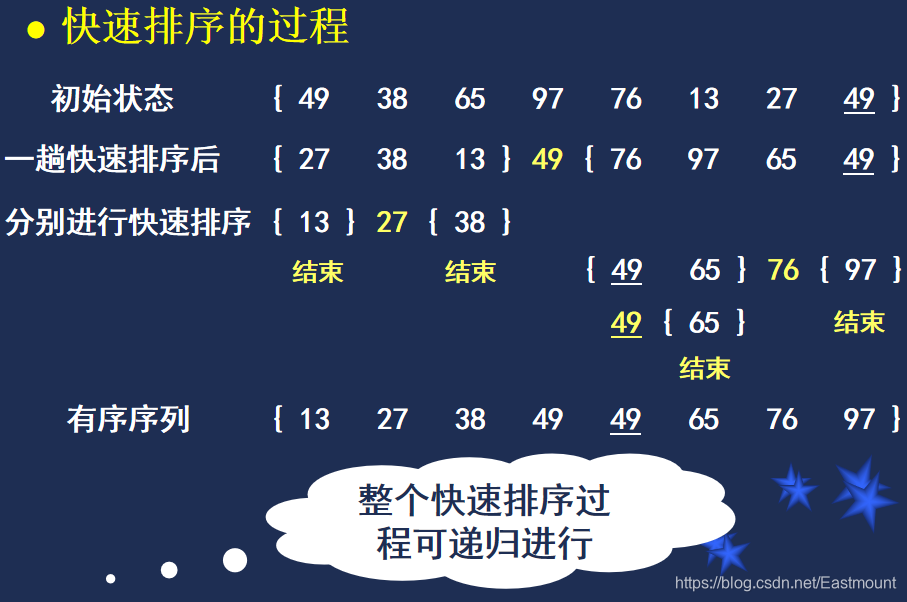
下面是一个简单的示例:
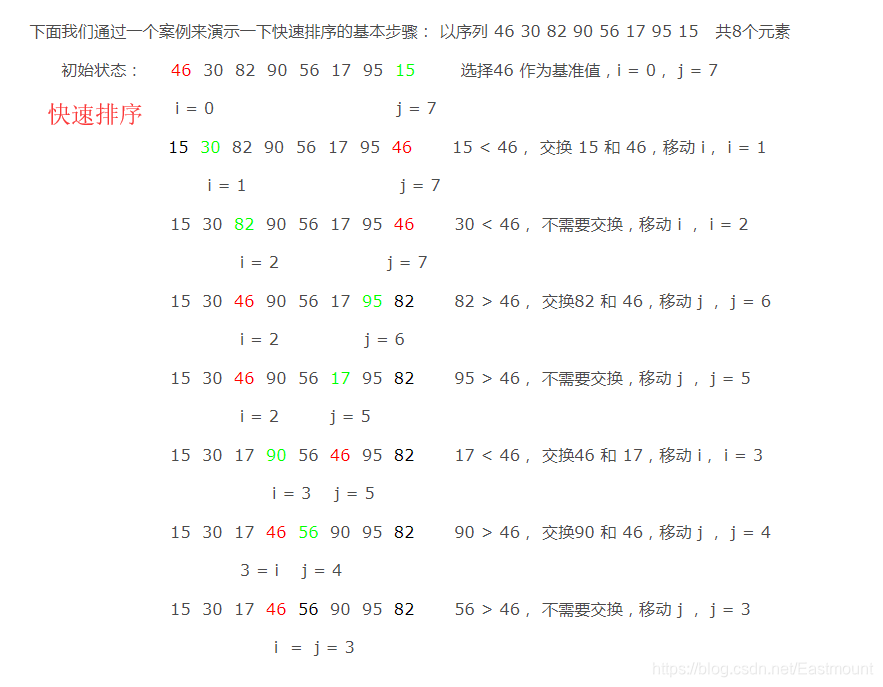
代码实现:
/*
* 快速排序
*
* 参数说明:
* a -- 待排序的数组
* l -- 数组的左边界(例如,从起始位置开始排序,则l=0)
* r -- 数组的右边界(例如,排序截至到数组末尾,则r=a.length-1)
*/
void quick_sort(int a[], int l, int r)
{
if (l < r)
{
int i,j,x;
i = l;
j = r;
x = a[i];
while (i < j)
{
while(i < j && a[j] > x)
j--; // 从右向左找第一个小于x的数
if(i < j)
a[i++] = a[j];
while(i < j && a[i] < x)
i++; // 从左向右找第一个大于x的数
if(i < j)
a[j--] = a[i];
}
a[i] = x;
quick_sort(a, l, i-1); /* 递归调用 */
quick_sort(a, i+1, r); /* 递归调用 */
}
}
举例1:
设一组初始关键字记录关键字为(20,15,14,18,21,36,40,10),则以20为基准记录的一趟快速排序结束后的结果为( )。
A.10,15,14,18,20,36,40,21
B.10,15,14,18,20,40,36,21
C.10,15,14,20,18,40,36,2l
D.10,15,14,18,20,36,40,21
解析:第一趟快排如下
20,15,14,18,21,36,40,10 => 右边开始,找到小于20的10,交换次序
10, 15,14,18,21,36,40,() => 左边继续,找到大于20的21,交换次序
10,15,14,18,(),36,40,21 => 右边继续找小于20的数字,找到()处停止
10,15,14,18,20,36,40,21 => 输出第一趟快速排序结果,故选D。
举例2:
设一组初始记录关键字序列(5,2,6,3,8),以第一个记录关键字5为基准进行一趟快速排序的结果为( 3,2,5,6,8 )。
解析:
快速排序5为基准,基本规则如下:left=5,right=8,先遍历right,寻找比基准5小的数字左移;找到之后与左边left下标替换,接着left向右移动,寻找比基准5大的数字,找到之后替换,最后left=right时,该数字与基准替换。
初始:5 2 6 3 8,right寻找到3,与left=5交换位置
接着:3 2 6 () 8,left从左边移动,找到6,与()替换位置
接着:3 2 () 6 8,此时向左移动right,right=left,停止快速排序,并用()替换基准5。
输出:3 2 5 6 8,其为第一趟快速排序的结果。
核心思想:选择最小、最大值并交换顺序

举例:
初始值为(38, 65, 97, 76, 13, 27, 10) 经过第3趟选择排序的最小值结果为___________。
解析:
第一趟结果:寻找最小值并交换顺序
10 65 97 76 13 27 38
第二趟结果:寻找第二个最小值并与第二个位置交换顺序
10 13 97 76 65 27 38
第三趟结果:寻找第三个最小值并与第三个位置交换顺序
10 13 27 76 65 97 38
核心思想:两两比较,交换顺序,每次能在最后一个位置获得最大值或最小值


举例:
初始值为(38, 65, 97, 76, 13, 27, 10) 经过第3趟冒泡排序的最小值结果为___________。
解析:
第一趟结果:
38 65 76 13 27 10 97
第二趟结果:
38 65 13 27 10 76 97
第三趟结果:
38 13 27 10 65 76 97
核心思想:寻找相应位置按顺序插入元素

算法实现过程:
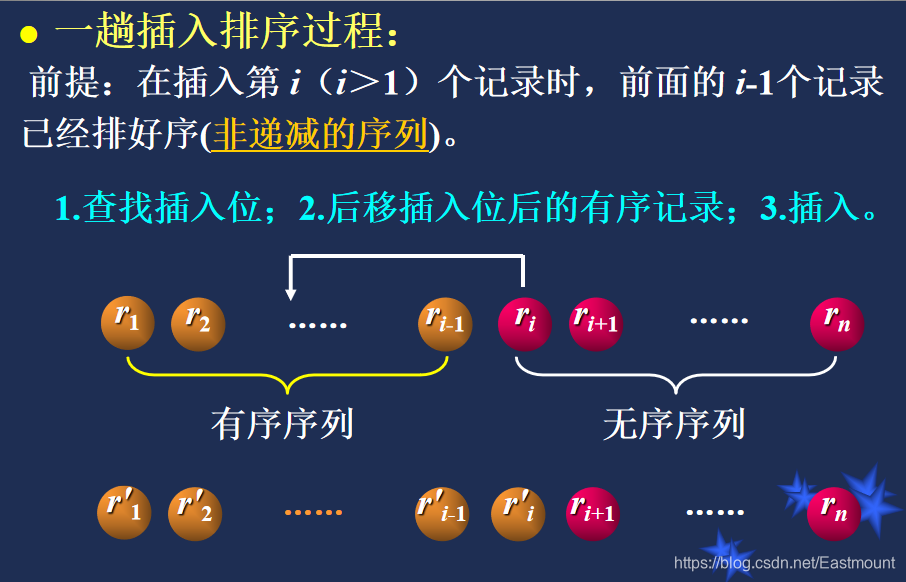
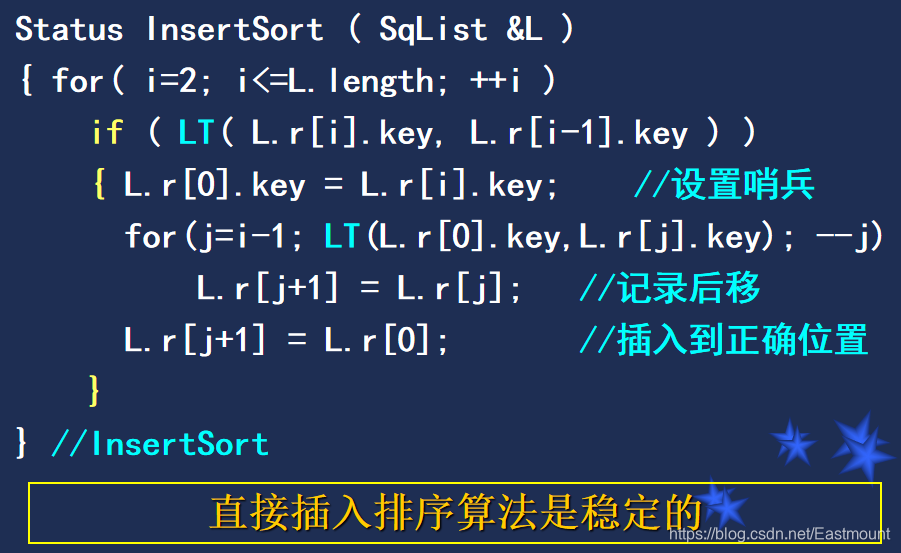
插入排序之希尔排序:
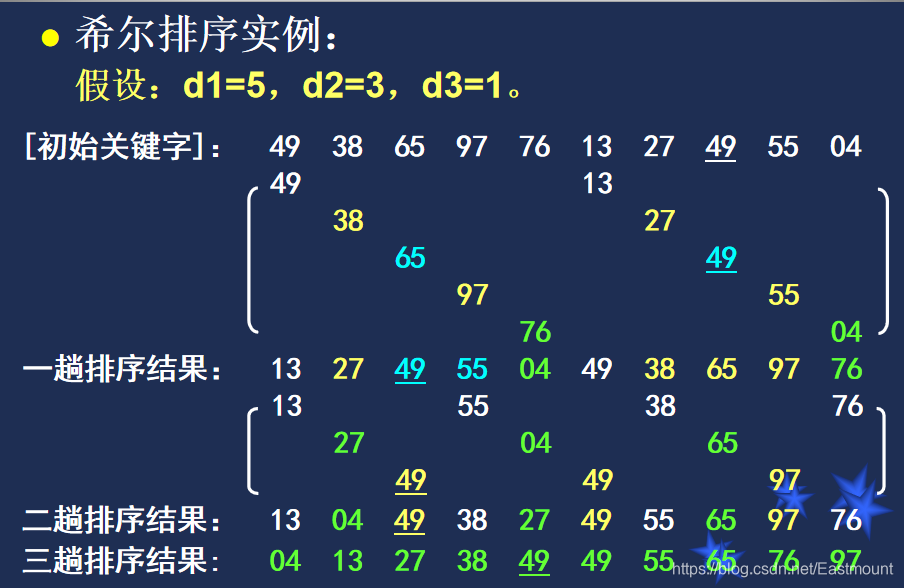
核心思想:分而治之再归并数据
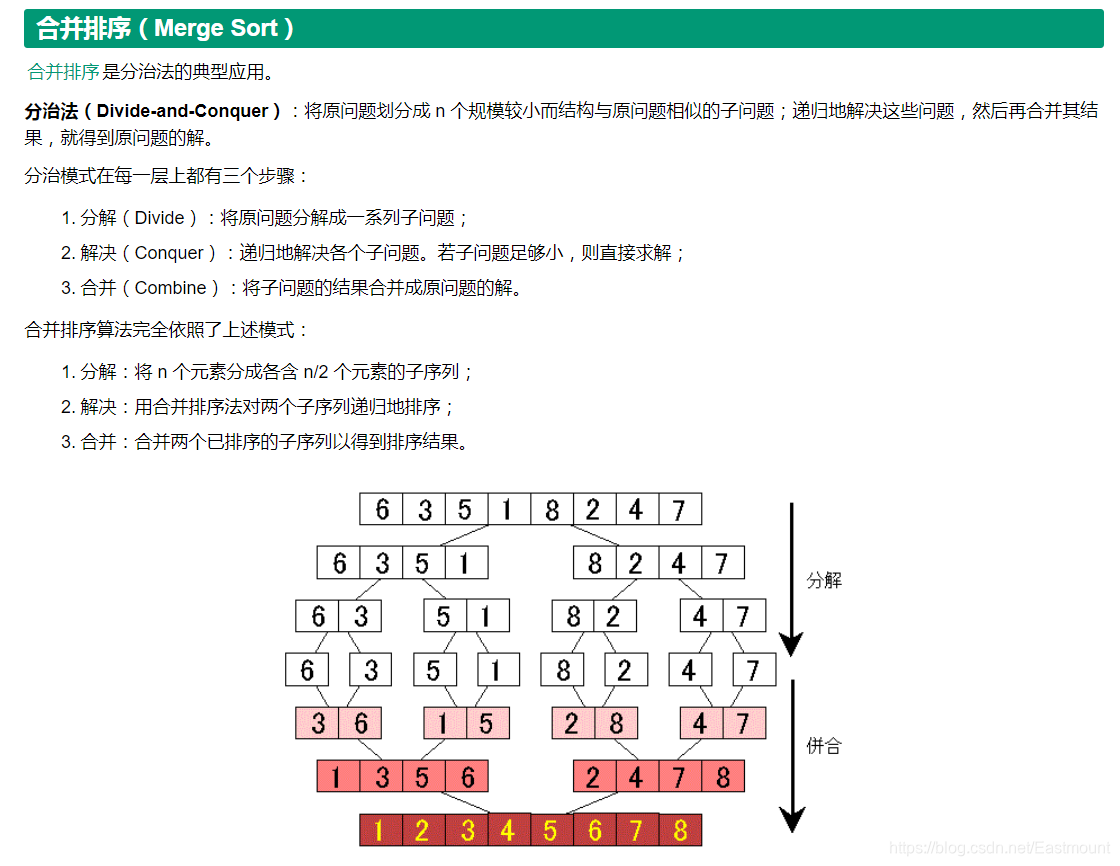
举例:
设一组初始记录关键字序列为(55,63,44,38,75,80,31,56),则利用筛选法建立的初始堆为___________________________。
答案:(31,38,54,56,75,80,55,63)
希望能与大家一起在华为云社区共同进步,加油!
原文地址:https://blog.csdn.net/Eastmount/article/details/88391773
(By:Eastmount 2021-08-02 深夜9点 http://blog.csdn.net/eastmount/ )
- 点赞
- 收藏
- 关注作者


评论(0)