对话功率谱与自相关函数

引入：

能量有限而平均功率为0的信号称之为能量信号；

能量无限而平均功率有限的信号称之为功率信号；（如周期信号）

能量谱密度：能量信号的能量在频域上的分布；

功率谱密度：功率信号的功率在频域上的分布；

二者与频谱的不同之处：

首先是计算结果的不同；

其次是频谱图上纵轴上表示的是能量或功率的大小而非信号幅度的大小；

计算能量谱密度以及功率谱密度：

能量谱密度：

功率谱密度：

信号的自相关函数：

同卷积的比较：

由上图可以看出，自相关函数可以通过卷积运算完成。

自相关函数反映了一个信号与其延迟了 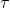 s后信号之间的相关程度，相关程度只和 时间差有关；

互相关函数反映了一个信号与另一个延迟了 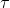 s 后的信号之间的相关程度，且仍然之和时间差  有关；

信号的自相关函数和信号的能量谱密度以及功率谱密度是互为傅里叶变换的，也就是说通过信号的自相关函数可以求得信号的能量谱密度以及功率谱密度，同样，通过信号的功率谱密度和能量谱密度也可以求得信号的自相关函数。

文章来源: reborn.blog.csdn.net，作者：李锐博恩，版权归原作者所有，如需转载，请联系作者。

原文链接：reborn.blog.csdn.net/article/details/80723671