离散傅里叶变换（DFT）（为了使用而学习的DFT）

1. 离散周期信号的傅里叶级数及其系数（DFS）

1）针对的对象：周期离散序列，设周期为N；

2）像连续周期信号那样用傅里叶级数表示信号，也即周期序列x[n]的傅里叶级数（DFS）表示：

其中：

从上面的公式中可以看到，积分限从0到N-1，而非像连续周期信号的傅里叶级数那样，从到，这是为什么呢？也就是说，为什么不像连续周期信号的傅里叶级数一样，需要无穷多个成谐波关系的复指数合成？

这是因为：

即对于n来说，是以N为周期的，所以只需要一个周期就可以了。

（连续周期信号的傅里叶变换要不要贴出来呢？）

3）下面在给出傅里叶系数的表达式：

（要不要推导一个这个式子怎么来的呢？）

注意：上面的DFS以及IDFS，自变量的取值范围都是从负无穷到正无穷。

之所以要先讲离散傅里叶级数，是因为它和离散傅里叶变换有看上去不小的联系呢，至少可以直观的、感官上地对比。

2. 离散傅里叶变换（DFT）

正变换公式（DFT）：

逆变换公式（IDFT）：

DFT的矩阵形式：

IDFT的矩阵形式：

对比DFS与DFT可以很明显的看到，二者之间的关系为：

除了取值范围不同，其他基本一致，实际应用中，要处理的信号大多数为有限长的非周期信号，因此DFT更常用。

DFT只不过是特殊的DFS，就是对DFS的时域和频域只取主值部分。

矩阵形式的DFT参考：浅谈离散傅里叶变换和快速算法

————————————————————————————————————————————————————

手稿版：

这部分参考：写的不错的博文

离散傅立叶级数（DFS）中的无限长序列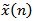和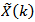都是以N为周期的周期序列，所以在计算离散时间周期序列及其频谱时，可以利用DFS的周期性，只需要在时域和频域各取一个主值序列，用计算机各计算一个周期中的N个样值，最后将所得的主值序列x（n）和X（k）进行周期延拓，即可得到原来的无限长序列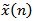和。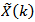

由DFT的导入过程可以发现，DFT不仅可以解决无限长周期序列的计算机运算问题，而且更可以解决有限长序列的计算机运算问题。事实上，对于有限长离散序列，总可以把时域和频域的变换区间（序列长度）均取为N（包括适当数量的补0点），通常把N称之为等间隔采样点数，我们可以把这个N点的变换区间视为某个周期序列的一个主值序列，直接利用DFT的定义计算其N点变换。

文章来源: reborn.blog.csdn.net，作者：李锐博恩，版权归原作者所有，如需转载，请联系作者。

原文链接：reborn.blog.csdn.net/article/details/80798926