內积空间
【摘要】 在讲內积空间之前，先提一下线性空间，这是內积空间的基础，也是我们学习任何一门理科所必备的常识。
线性空间介绍：
向量空间亦称向量空间。它是线性代数的中心内容和基本概念之一。设V是一个非空集合，P是一个域。若：
1.在V中定义了一种运算，称为加法，即对V中任意两个元素α与β都按...
在讲內积空间之前，先提一下线性空间，这是內积空间的基础，也是我们学习任何一门理科所必备的常识。
线性空间介绍：
向量空间亦称向量空间。它是线性代数的中心内容和基本概念之一。设V是一个非空集合，P是一个域。若：
2.在P与V的元素间定义了一种运算，称为纯量乘法(亦称数量乘法)，即对V中任意元素α和P中任意元素k，都按某一法则对应V内惟一确定的一个元素kα，称为k与α的积。
3.加法与纯量乘法满足以下条件：
1) α+β=β+α，对任意α，β∈V.
2) α+(β+γ)=(α+β)+γ，对任意α，β，γ∈V.
3) 存在一个元素0∈V，对一切α∈V有α+0=α，元素0称为V的零元.
4) 对任一α∈V，都存在β∈V使α+β=0，β称为α的负元素，记为-α.
5) 对P中单位元1，有1α=α(α∈V).
6) 对任意k，l∈P，α∈V有(kl)α=k(lα).
7) 对任意k，l∈P，α∈V有(k+l)α=kα+lα.
8) 对任意k∈P，α，β∈V有k(α+β)=kα+kβ，
则称V为域P上的一个线性空间，或向量空间。V中元素称为向量，V的零元称为零向量，P称为线性空间的基域.当P是实数域时，V称为实线性空间.当P是复数域时，V称为复线性空间。
各个版本大同小异，都是一个意思，这里就选百度百科上的描述吧。
————————————————————————————————————————————————————
內积空间：
也就是说在线性空间上装配上內积，线性空间也就成了內积空间了，內积是什么东西？
內积是一种运算，将线性空间中的两个元素映射成一个元素，即二元映射为一元，且这种运算满足所谓的內积公理，则这种运算才能称为內积。
內积对第二变元具有共轭线性性质，要记住，区分內积对第一变元和第二变元不同的运算规则。
下面列出一些常用的內积：
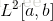的意思是在区间[a,b]上平方可积的全体函数。
————————————————————————————————————————————————————
內积空间中的柯西—施瓦兹不等式：
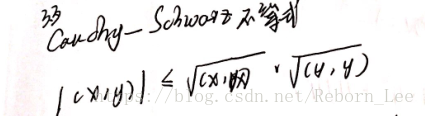
由于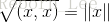 
故上面的Cauchy_Schwarz不等式可以写成：
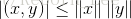
介绍这个不等式的目的如下，就是证明由內积诱导（定义）的范数是否满足范数公理，如果满足，这范数可以由內积来诱导。
问题如下：
证明：
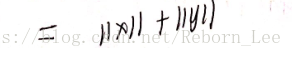
既然知道由內积可以诱导范数，那么下面的公式自然不难验证了：
左边由內积表示出来，然后经过一系列的化简，即可得到右边的式子。
废话不多说，直接上图：
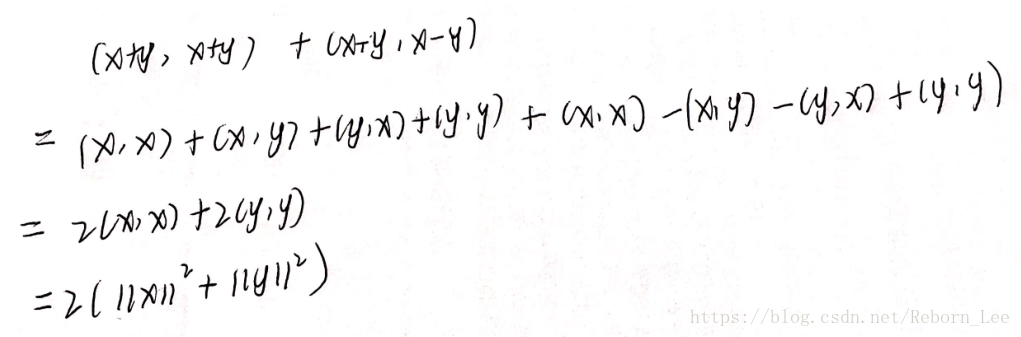
就到这里吧，下一篇看看正交分解以及正交投影：正交分解。
文章来源: reborn.blog.csdn.net，作者：李锐博恩，版权归原作者所有，如需转载，请联系作者。
原文链接：reborn.blog.csdn.net/article/details/80925262
【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱：
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者
评论（0）