非线性方程求根的牛顿法
【摘要】 牛顿迭代法的推导:
线性方程容易求解,但对于非线性方程,若能用某个线性方程来近似,求出该线性方程的解,即可得到原非线性方程的一个近似解。
设已知非线性函数的一个近似零点是,用在该点的Taylor展开式的线性部分来近似,即得到:
将线性近似函数的零点记作,并作为的一个新零点,有:
如此反复,得到求解非线性方程=0的迭代公式:
称为牛顿迭代公式。
显然牛顿迭代公式要求在根的...
牛顿迭代法的推导:
线性方程容易求解,但对于非线性方程,若能用某个线性方程来近似,求出该线性方程的解,即可得到原非线性方程的一个近似解。
设已知非线性函数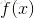 的一个近似零点是
的一个近似零点是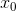 ,用
,用 在该点的Taylor展开式的线性部分来近似
在该点的Taylor展开式的线性部分来近似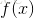 ,即得到:
,即得到:
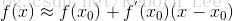
将线性近似函数的零点记作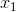 ,并作为
,并作为 的一个新零点,有:
的一个新零点,有:
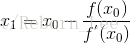
如此反复,得到求解非线性方程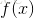 =0的迭代公式:
=0的迭代公式:

称为牛顿迭代公式。
显然牛顿迭代公式要求在根 的某个领域内,函数
的某个领域内,函数 的一阶导数
的一阶导数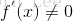 .
.
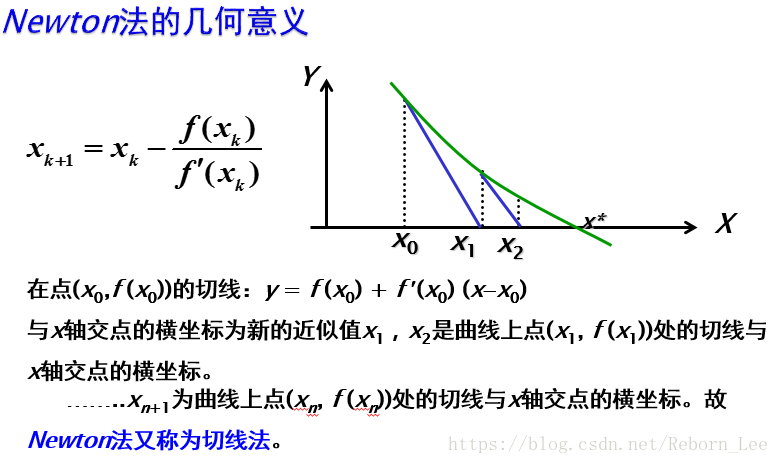
牛顿迭代法的几何意义:
举例理解牛顿迭代法:

牛顿法收敛定理:

定理表明:

先说到这里,用到再补充。
文章来源: reborn.blog.csdn.net,作者:李锐博恩,版权归原作者所有,如需转载,请联系作者。
原文链接:reborn.blog.csdn.net/article/details/80960491
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)