时序分析之静态分析基础
目录
（数据输出延时）（触发器从时钟有效，数据从输入到达输出的时间）和缓冲延时
发射沿（launch edge）与锁存沿（latch edge）
静态时序分析（SAT）
静态时序分析的前提就是设计者先提出要求，然后时序分析工具才会根据特定的时序模型进行分析，给出正确是时序报告。
进行静态时序分析，主要目的就是为了提高系统工作主频以及增加系统的稳定性。对很多数字电路设计来说，提高工作频率非常重要，因为高工作频率意味着高处理能力。通过附加约束可以控制逻辑的综合、映射、布局和布线，以减小逻辑和布线延时，从而提高工作频率。
相关参数分析
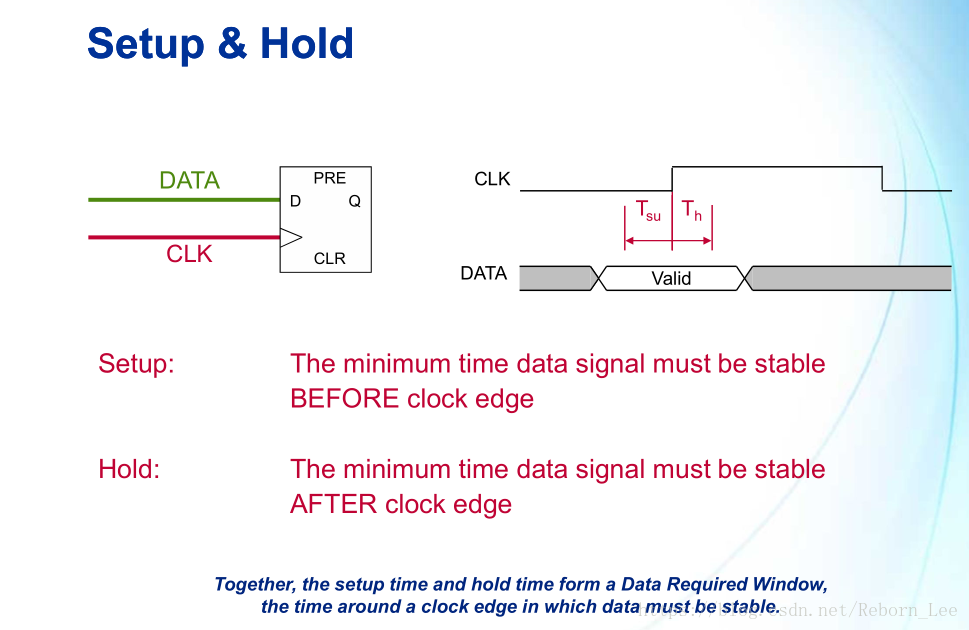
如下图所示，建立时间就是时钟有效沿到来之前数据必须保持稳定的最小时间；
保持时间就是时钟有效沿到来之后数据必须保持稳定的最小时间；
是指时钟触发开始到有效数据输出的器件内部所有延时的总和。或简单地说：在时钟有效后，D的数据并不能立即传到Q端，这段等待的时间就是触发器的时钟到输出时间。
（这个时间指的是当时钟有效沿变化后，数据从输入端到输出端的最小时间间隔。）
而缓冲延时是指信号经过缓冲器到达有效的电压输出所需要的时间。
二者之间有所区别：
除了包含缓冲延时，还包括逻辑延时。
如下图：给出确定的方法，zai在输出缓冲的末端直接相连一个测量负载，最常见的是50欧姆的电阻或30pF的电容，然后测量负载上的信号电压到达一定电平所需要的时间，这个电平称为测量电压（Vms），一般是信号高电平的一半。
时序分析起点（launch edge）：第一级寄存器数据变化的时钟边沿，也是静态时序分析的起点。
时序分析终点（latch edge）：数据锁存的时钟边沿，也是静态时序分析的终点。
如下图：
时钟到达时间就是指时钟从latch edge到达目的寄存器（destination register）输入端所用的时间。
这里不考虑这个建立不定态（Setup Uncertainty）；
- （保持）（hold）数据需求时间
；
上图中的Hold Uncertainty这里不考虑。
下面这幅图画出了建立余量（Setup Slack）的示意图：
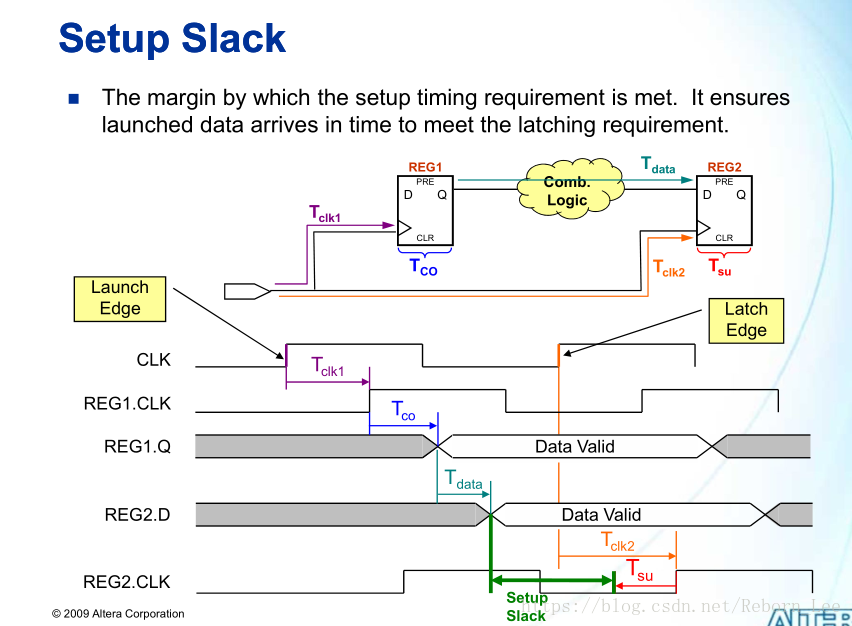
下面这幅图根据上图给出了建立余量（Setup Slack）的计算公式，但是还不够清晰。下面我们认真解读一下：
我们通过上面的介绍已经知道了建立（Setup）数据需求时间（Data Required Time）为：
；
而数据到达时间（Data Arrival Time）为：
；
那么建立余量（Setup Slack）为：
这里假设时钟偏斜（Clock Skew）为0，也就是，同时（这是很好理解的，这两个边沿之间的距离恰好是一个时钟周期）；
（下面这个公式很重要！与其记推导公式，不如记下面这个公式来的直接，明显！）
对应的区域位于上图的绿色部分！
这个最终结果说明了源寄存器与目的寄存器之间延迟 不能太长的原因，延迟越长，slack越小。
从上图公式下面还有这样的信息：
当建立余量为正时，满足时序要求，否则不满足。
保持余量的分析方法与建立时间余量的分析方法如出一辙，简单看下，这个相对于建立时间余量要好理解一点，至少比较直观。
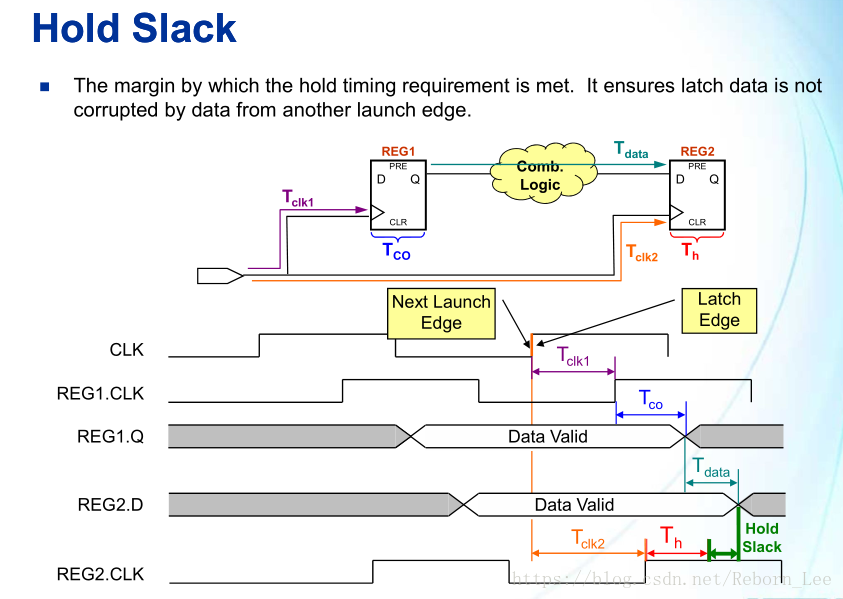
同样，我们先看看数据到达时间以及保持（Hold）数据需求时间（Data Required Time）：
；
；
如此以来，我们就可以得到保持余量（Hold Slack）为：
这里：
从最终结果可以看出，这就是源寄存器与目的寄存器之间延迟不能太短的原因，时间太短，Hold Slack越小。
同样从上图可以知道，余量结果为正，则满足时序要求，否则不满足。
参考文献：
Altera时序分析相关资料
文章来源: reborn.blog.csdn.net，作者：李锐博恩，版权归原作者所有，如需转载，请联系作者。
原文链接：reborn.blog.csdn.net/article/details/81461955
- 点赞
- 收藏
- 关注作者
评论（0）