【 MATLAB 】信号处理工具箱之 fft 案例分析

上篇博文：【 MATLAB 】信号处理工具箱之fft简介及案例分析介绍了MATLAB信号处理工具箱中的信号变换 fft 并分析了一个案例，就是被噪声污染了的信号的频谱分析。

这篇博文继续分析几个小案例：

Gaussian Pulse

这个案例是将高斯脉冲从时域变换到频域，高斯脉冲的信息在下面的程序中都有注释：

  

   

    

     

    
    

     

      clc
     
    
   

    

     

    
    

     

      clear
     
    
   

    

     

    
    

     

      close all
     
    
   

    

     

    
    

     

      % Convert a Gaussian pulse from the time domain to the frequency domain.
     
    
   

    

     

    
    

     

      % 
     
    
   

    

     

    
    

     

      % Define signal parameters and a Gaussian pulse, X.
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      Fs = 100; % Sampling frequency
     
    
   

    

     

    
    

     

      t = -0.5:1/Fs:0.5;  % Time vector 
     
    
   

    

     

    
    

     

      L = length(t); % Signal length
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      X = 1/(4*sqrt(2*pi*0.01))*(exp(-t.^2/(2*0.01)));
     
    
   

    

     

    
    

     

      % Plot the pulse in the time domain.
     
    
   

    

     

    
    

     

      figure();
     
    
   

    

     

    
    

     

      plot(t,X)
     
    
   

    

     

    
    

     

      title('Gaussian Pulse in Time Domain')
     
    
   

    

     

    
    

     

      xlabel('Time (t)')
     
    
   

    

     

    
    

     

      ylabel('X(t)')
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      % To use the fft function to convert the signal to the frequency domain, 
     
    
   

    

     

    
    

     

      % first identify a new input length that is the next power of 2 from the original signal length. 
     
    
   

    

     

    
    

     

      % This will pad the signal X with trailing zeros in order to improve the performance of fft.
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      n = 2^nextpow2(L);
     
    
   

    

     

    
    

     

      % Convert the Gaussian pulse to the frequency domain.
     
    
   

    

     

    
    

     

      % 
     
    
   

    

     

    
    

     

      Y = fft(X,n);
     
    
   

    

     

    
    

     

      % Define the frequency domain and plot the unique frequencies.
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      f = Fs*(0:(n/2))/n;
     
    
   

    

     

    
    

     

      P = abs(Y/n);
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      figure();
     
    
   

    

     

    
    

     

      plot(f,P(1:n/2+1)) 
     
    
   

    

     

    
    

     

      title('Gaussian Pulse in Frequency Domain')
     
    
   

    

     

    
    

     

      xlabel('Frequency (f)')
     
    
   

    

     

    
    

     

      ylabel('|P(f)|')
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
  
 

高斯脉冲在时域的图像：

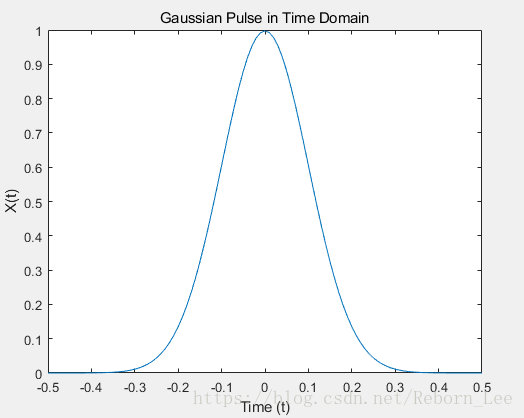
高斯脉冲在频域的图像：

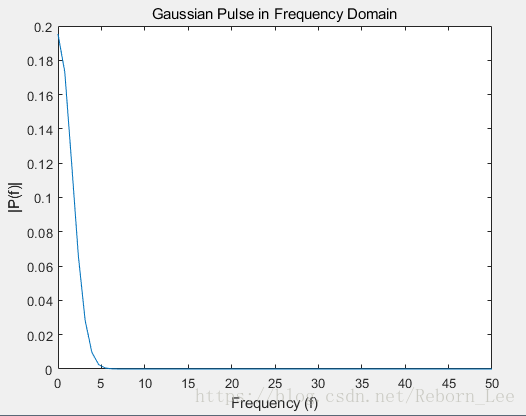
Cosine Waves

这个例子比较简单，就是不同频率的余弦波在时域以及频域的比较：

  

   

    

     

    
    

     

      clc
     
    
   

    

     

    
    

     

      clear
     
    
   

    

     

    
    

     

      close all
     
    
   

    

     

    
    

     

      % Compare cosine waves in the time domain and the frequency domain.
     
    
   

    

     

    
    

     

      % 
     
    
   

    

     

    
    

     

      % Specify the parameters of a signal with a sampling frequency of 1kHz and a signal duration of 1 second.
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      Fs = 1000; % Sampling frequency
     
    
   

    

     

    
    

     

      T = 1/Fs; % Sampling period
     
    
   

    

     

    
    

     

      L = 1000; % Length of signal
     
    
   

    

     

    
    

     

      t = (0:L-1)*T; % Time vector
     
    
   

    

     

    
    

     

      % Create a matrix where each row represents a cosine wave with scaled frequency. 
     
    
   

    

     

    
    

     

      % The result, X, is a 3-by-1000 matrix. The first row has a wave frequency of 50, 
     
    
   

    

     

    
    

     

      % the second row has a wave frequency of 150, and the third row has a wave frequency of 300.
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      x1 = cos(2*pi*50*t); % First row wave
     
    
   

    

     

    
    

     

      x2 = cos(2*pi*150*t); % Second row wave
     
    
   

    

     

    
    

     

      x3 = cos(2*pi*300*t); % Third row wave
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      X = [x1; x2; x3];
     
    
   

    

     

    
    

     

      % Plot the first 100 entries from each row of X in a single figure in order and compare their frequencies.
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      figure();
     
    
   

    

     

    
    

     

      for i = 1:3
     
    
   

    

     

    
    

     

       subplot(3,1,i)
     
    
   

    

     

    
    

     

       plot(t(1:100),X(i,1:100))
     
    
   

    

     

    
    

     

       title(['Row ',num2str(i),' in the Time Domain'])
     
    
   

    

     

    
    

     

      end
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      % For algorithm performance purposes, fft allows you to pad the input with trailing zeros. 
     
    
   

    

     

    
    

     

      % In this case, pad each row of X with zeros so that the length of each row is the next higher power of 2 from the current length. 
     
    
   

    

     

    
    

     

      % Define the new length using the nextpow2 function.
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      n = 2^nextpow2(L);
     
    
   

    

     

    
    

     

      % Specify the dim argument to use fft along the rows of X, that is, for each signal.
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      dim = 2;
     
    
   

    

     

    
    

     

      % Compute the Fourier transform of the signals.
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      Y = fft(X,n,dim);
     
    
   

    

     

    
    

     

      % Calculate the double-sided spectrum and single-sided spectrum of each signal.
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      P2 = abs(Y/L);
     
    
   

    

     

    
    

     

      P1 = P2(:,1:n/2+1);
     
    
   

    

     

    
    

     

      P1(:,2:end-1) = 2*P1(:,2:end-1);
     
    
   

    

     

    
    

     

      % In the frequency domain, plot the single-sided amplitude spectrum for each row in a single figure.
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      figure();
     
    
   

    

     

    
    

     

      for i=1:3
     
    
   

    

     

    
    

     

       subplot(3,1,i)
     
    
   

    

     

    
    

     

       plot(0:(Fs/n):(Fs/2-Fs/n),P1(i,1:n/2))
     
    
   

    

     

    
    

     

       title(['Row ',num2str(i),' in the Frequency Domain'])
     
    
   

    

     

    
    

     

      end
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
  
 

下图是频率为50Hz，150Hz以及300Hz的余弦波在时域的图像：

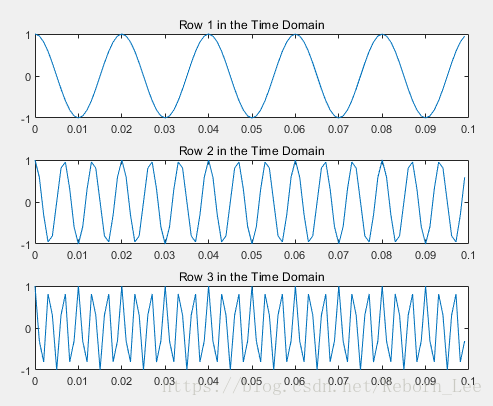
下图分别为其fft：

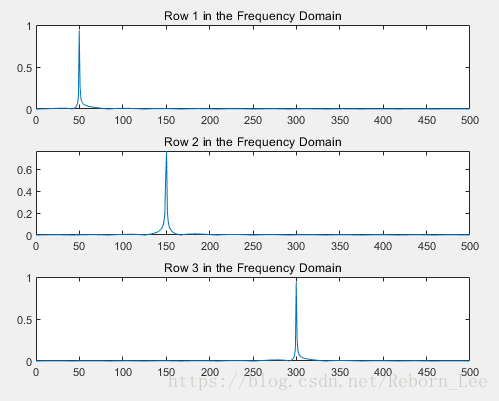
从频域图中可以清晰的看到它们的频率成分位于何处。

文章来源: reborn.blog.csdn.net，作者：李锐博恩，版权归原作者所有，如需转载，请联系作者。

原文链接：reborn.blog.csdn.net/article/details/83060448