【 MATLAB 】使用 MATLAB 实现模拟信号的近似及其连续傅里叶变换

严格来说，利用MATLAB是不可能用来分析模拟信号的。然而，如果有足够小的时间增量在足够细的栅格上对采样而产生一种平滑的图，并有足够大的时间来展示所有的模式，那么就能对模拟信号作近似分析。令是栅格间隔并且有，那么

就能用作一个数组对一个模拟信号进行仿真。不应该将采样间隔Ts与栅格间隔混淆，是严格用来在MATLAB中表示一个模拟信号的。类似的，连续时间傅里叶变换（CTFT）：

也可以是近似的，如下所示：

现在，如果为有限长，那么上式：

就类似于离散时间傅里叶变换关系，离散时间傅里叶关系，之前有博文对此总结：【 MATLAB 】用 MATLAB 实现离散时间傅里叶变换（DTFT）的两个案例分析

这篇博文中的第二个案例。

  

   

    

     

    
    

     

      k = [0:M];
     
    
   

    

     

    
    

     

      n = [n1:n2];
     
    
   

    

     

    
    

     

      X = x * (exp(-j * pi/M)).^(n'*k);
     
    
   

    

     

    
    

     

    
  
 

下面给出一个案例：

设

使用MATLAB求出并画出它的傅里叶变换。

题解：

通过公式计算，可以得出：

                         (1)

这里，估计出栅格间隔以及信号的带宽最为重要。

为了对作数值计算，必须首先用一个有限长的栅格序列近似.

利用近似式 ,可以注意到可以近似为在[-0.005,0.005]（或等效为在[-5,5]毫秒上）的有限长信号。同样，根据（1）式，,这意味着信号的带宽为2000Hz，所以选栅格间隔

这里解释下，上面的1/2（2000）代表的是采样间隔，栅格间隔要远小于采样间隔。

这样，我们就可以给出MATLAB脚本了：

  

   

    

     

    
    

     

      clc
     
    
   

    

     

    
    

     

      clear
     
    
   

    

     

    
    

     

      close all
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      % Analog signal
     
    
   

    

     

    
    

     

      Dt = 0.00005;
     
    
   

    

     

    
    

     

      t = - 0.005:Dt:0.005;
     
    
   

    

     

    
    

     

      xa = exp(-1000 * abs(t));
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      % Continuous_time Fourier Transform
     
    
   

    

     

    
    

     

      Wmax = 2*pi*2000;
     
    
   

    

     

    
    

     

      K = 500;
     
    
   

    

     

    
    

     

      k = 0:1:K;
     
    
   

    

     

    
    

     

      W = k*Wmax/K;
     
    
   

    

     

    
    

     

      Xa = xa * exp(-j * t' * W)*Dt;
     
    
   

    

     

    
    

     

      Xa = real(Xa);
     
    
   

    

     

    
    

     

      W = [-fliplr(W),W(2:501)];
     
    
   

    

     

    
    

     

      Xa = [fliplr(Xa),Xa(2:501)];
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      subplot(2,1,1)
     
    
   

    

     

    
    

     

      plot(t*1000,xa);
     
    
   

    

     

    
    

     

      xlabel('t in msec');ylabel('xa(t)');
     
    
   

    

     

    
    

     

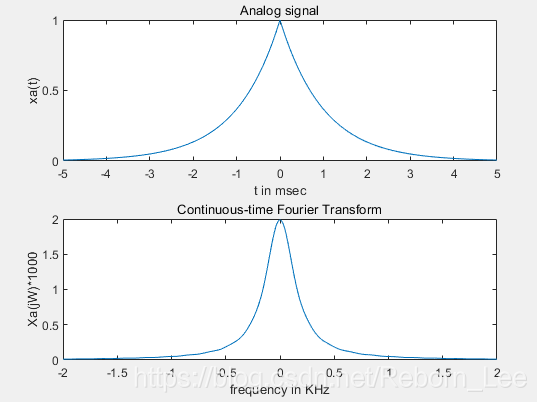
      title('Analog signal');
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      subplot(2,1,2)
     
    
   

    

     

    
    

     

      plot(W/(2*pi*1000),Xa*1000);
     
    
   

    

     

    
    

     

      xlabel('frequency in KHz');ylabel('Xa(jW)*1000');
     
    
   

    

     

    
    

     

      title('Continuous-time Fourier Transform');
     
    
  
 

文章来源: reborn.blog.csdn.net，作者：李锐博恩，版权归原作者所有，如需转载，请联系作者。

原文链接：reborn.blog.csdn.net/article/details/83387192