ppval

Evaluate piecewise polynomial

Syntax

v = ppval(pp,xq)

Description

v = ppval(pp,xq) evaluates the piecewise polynomial pp at the query points xq.

v = ppval(pp,xq) 评估查询点xq处的分段多项式pp。

Create Piecewise Polynomial with Polynomials of Several Degrees

Create a piecewise polynomial that has a cubic polynomial in the interval [0,4], a quadratic polynomial in the interval [4,10], and a quartic polynomial in the interval [10,15].

创建在区间[0,4]中具有三次多项式的分段多项式，区间[4,10]中的二次多项式，以及区间[10,15]中的四次多项式。

breaks = [0 4 10 15];
coefs = [0 1 -1 1 1; 0 0 1 -2 53; -1 6 1 4 77];
pp = mkpp(breaks,coefs)

Evaluate the piecewise polynomial at many points in the interval [0,15] and plot the results. Plot vertical dashed lines at the break points where the polynomials meet.
xq = 0:0.01:15;
plot(xq,ppval(pp,xq))
line([4 4],ylim,'LineStyle','--','Color','k')
line([10 10],ylim,'LineStyle','--','Color','k')

Create Piecewise Polynomial with Repeated Pieces

Create and plot a piecewise polynomial with four intervals that alternate between two quadratic polynomials.
The first two subplots show a quadratic polynomial and its negation shifted to the intervals [-8,-4] and [-4,0]. The polynomial is

创建并绘制具有四个间隔的分段多项式，这两个间隔在两个二次多项式之间交替。
前两个子图显示二次多项式，其否定移位到区间[-8，-4]和[-4,0]。 多项式是

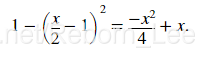
The third subplot shows a piecewise polynomial constructed by alternating these two quadratic pieces over four intervals. Vertical lines are added to show the points where the polynomials meet.

第三个子图显示了通过在四个间隔上交替这两个二次曲线构造的分段多项式。 添加垂直线以显示多项式相交的点。
subplot(2,2,1)
cc = [-1/4 1 0]; 
pp1 = mkpp([-8 -4],cc);
xx1 = -8:0.1:-4; 
plot(xx1,ppval(pp1,xx1),'k-')

subplot(2,2,2)
pp2 = mkpp([-4 0],-cc);
xx2 = -4:0.1:0; 
plot(xx2,ppval(pp2,xx2),'k-')

subplot(2,1,2)
pp = mkpp([-8 -4 0 4 8],[cc;-cc;cc;-cc]);
xx = -8:0.1:8;
plot(xx,ppval(pp,xx),'k-')
hold on
line([-4 -4],ylim,'LineStyle','--')
line([0 0],ylim,'LineStyle','--')
line([4 4],ylim,'LineStyle','--')
hold off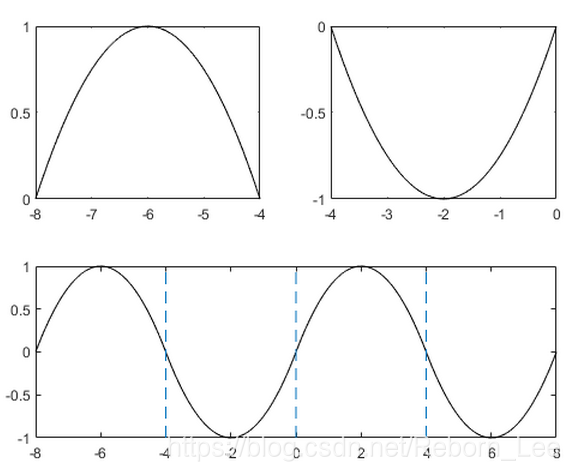

Input Arguments

pp — Piecewise polynomial
structure

Piecewise polynomial, specified as a structure. You can create pp using spline, pchip, interp1, or the spline utility function mkpp.

分段多项式，指定为结构。 您可以使用样条线，pchip，interp1或样条函数函数mkpp创建pp。

xq — Query points
vector | array

Query points, specified as a vector or array. xq specifies the points where ppval evaluates the piecewise polynomial.

查询点，指定为矢量或数组。 xq指定ppval评估分段多项式的点。

Data Types: single | double

Output Arguments

v — Piecewise polynomial values at query points
vector | matrix | array

Piecewise polynomial values at query points, returned as a vector, matrix, or array.

If pp has [d1,..,dr]-valued coefficients (nonscalar coefficient values), then:

• When xq is a vector of length N, v has size [d1,...,dr,N], and v(:,...,:,j) is the value at xq(j).

• When xq has size [N1,...,Ns], v has size [d1,...,dr,N1,...,Ns], and v(:,...,:, j1,...,js) is the value at xq(j1,...,js).

文章来源: reborn.blog.csdn.net，作者：李锐博恩，版权归原作者所有，如需转载，请联系作者。

原文链接：reborn.blog.csdn.net/article/details/83421657