residuez

Z-transform partial-fraction expansion

Syntax

[r,p,k] = residuez(b,a)
[b,a] = residuez(r,p,k) 

Description

residuez converts a discrete time system, expressed as the ratio of two polynomials, to partial fraction expansion, or residue, form. It also converts the partial fraction expansion back to the original polynomial coefficients.

residualz将离散时间系统（表示为两个多项式的比率）转换为部分分数扩展或留数形式。 它还将部分分数展开转换回原始多项式系数。

[r,p,k] = residuez(b,a) finds the residues, poles, and direct terms of a partial fraction expansion of the ratio of two polynomials, b(z) and a(z). Vectors b and a specify the coefficients of the polynomials of the discrete-time system b(z)/a(z) in descending powers of z.

[r,p,k] = residuez(b,a) 求出两个多项式b（z）和a（z）的比率的部分分数展开的留数，极点和直接项。 向量b和a以z的下降幂指定离散时间系统b（z）/ a（z）的多项式的系数。

上面的描述中我把所有的 residues 都翻译成了留数，事实上，我觉得这既不是一个中国词，又不是一个外国词，就是翻译者的意淫。

英文单词：residue 

• n.残渣；残余物；【数】残数；【化】残基

• 网络残留物；留数；剩余物

• 变形复数：residues；

从这个翻译中我们可以看出它就是一个残留数，大概就是留的来源吧。

如下：

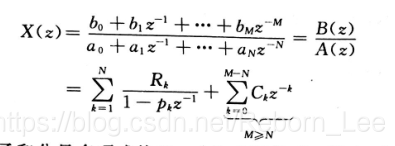
分子多项式除以分母多项式，得到第一项就是残留项，分子上的数就是残留数，就是所谓的留数，就这点东西，弄个留数，吓唬谁呢？

这个函数就是用来辅助处理 z变换的，一般而言，求解z反变换，按照定义求解一个围线积分，没人愿意用这种积分来恶心自己吧。于是我们可以使用部分分式分解，以及常用的z变换以及z变换的性质来求解z反变换。

部分分式分解，如上式，我们就遇到了留数和极点问题，这时我们就用本博文介绍的函数residuez来辅助求解。

下面这张图节选自课本上的一部分，大概看下即可。

继续上面的内容，刚刚是得到了b和a向量。

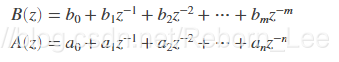
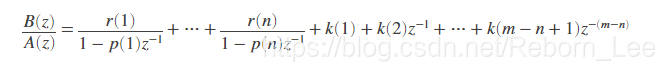
The returned column vector r contains the residues, column vector p contains the pole locations, and row vector k contains the direct terms. The number of poles is

n = length(a)-1 = length(r) = length(p)

The direct term coefficient vector k is empty if length(b) is less than length(a); otherwise:

length(k) = length(b) - length(a) + 1

If p(j) = ... = p(j+s-1) is a pole of multiplicity s, then the expansion includes terms of the form

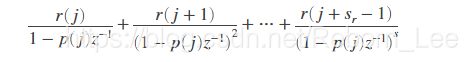
[b,a] = residuez(r,p,k) with three input arguments and two output arguments, converts the partial fraction expansion back to polynomials with coefficients in row vectors b and a.

最后帮助文档说了一句话：

The residue function in the standard MATLAB® language is very similar to residuez. It computes the partial fraction expansion of continuous-time systems in the Laplace domain (see reference [1]), rather than discrete-time systems in the z-domain as does residuez.

它的意思是还有一个类似的函数叫 residue，这个函数是处理Laplace变换的。

想了解，自己去看！

这篇博文就到这里，具体的案例见下篇博文。

文章来源: reborn.blog.csdn.net，作者：李锐博恩，版权归原作者所有，如需转载，请联系作者。

原文链接：reborn.blog.csdn.net/article/details/83446437