【 MATLAB 】通过不同样本数的同一个有限长序列作 DTFT 对比

上篇博文我们讨论了：【 MATLAB 】使用 MATLAB 得到高密度谱（补零得到DFT）和高分辨率谱（获得更多的数据得到DFT）的方式对比（附MATLAB脚本）

可是还是觉得不过瘾，还有下面的情况需要对比。于是就有了这篇博文。

案例：

想要基于有限样本数来确定他的频谱。

下面我们分如下几种情况来分别讨论：

a. 求出并画出  的DTFT；

b. 求出并画出  的DTFT；

  

   

    

     

    
    

     

      clc;clear;close all;
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      n = 0:99;
     
    
   

    

     

    
    

     

      x = cos(0.48*pi*n) + cos(0.52*pi*n);
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      n1 = 0:9;
     
    
   

    

     

    
    

     

      y1 = x(1:10);
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      subplot(2,2,1)
     
    
   

    

     

    
    

     

      stem(n1,y1);
     
    
   

    

     

    
    

     

      title('signal x(n), 0 <= n <= 9');
     
    
   

    

     

    
    

     

      xlabel('n');ylabel('x(n) over n in [0,9]');
     
    
   

    

     

    
    

     

      Y1 = dft(y1,10);
     
    
   

    

     

    
    

     

      magY1 = abs(Y1);
     
    
   

    

     

    
    

     

      k1 = 0:1:9;
     
    
   

    

     

    
    

     

      N = 10;
     
    
   

    

     

    
    

     

      w1 = (2*pi/N)*k1;
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      subplot(2,2,2);
     
    
   

    

     

    
    

     

      % stem(w1/pi,magY1);
     
    
   

    

     

    
    

     

      % title('DFT of x(n) in [0,9]');
     
    
   

    

     

    
    

     

      % xlabel('frequency in pi units');
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      %In order to clearly see the relationship between DTFT and DFT, we draw DTFT on the same picture.
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      %Discrete-time Fourier Transform
     
    
   

    

     

    
    

     

      K = 500;
     
    
   

    

     

    
    

     

      k = 0:1:K;
     
    
   

    

     

    
    

     

      w = 2*pi*k/K; %plot DTFT in [0,2pi];
     
    
   

    

     

    
    

     

      X = y1*exp(-j*n1'*w);
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      magX = abs(X);
     
    
   

    

     

    
    

     

      % hold on 
     
    
   

    

     

    
    

     

      plot(w/pi,magX);
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      % hold off
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      subplot(2,2,3)
     
    
   

    

     

    
    

     

      stem(n,x);
     
    
   

    

     

    
    

     

      title('signal x(n), 0 <= n <= 99');
     
    
   

    

     

    
    

     

      xlabel('n');ylabel('x(n) over n in [0,99]');
     
    
   

    

     

    
    

     

      Xk = dft(x,100);
     
    
   

    

     

    
    

     

      magXk = abs(Xk);
     
    
   

    

     

    
    

     

      k1 = 0:1:99;
     
    
   

    

     

    
    

     

      N = 100;
     
    
   

    

     

    
    

     

      w1 = (2*pi/N)*k1;
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      subplot(2,2,4);
     
    
   

    

     

    
    

     

      % stem(w1/pi,magXk);
     
    
   

    

     

    
    

     

      % title('DFT of x(n) in [0,99]');
     
    
   

    

     

    
    

     

      % xlabel('frequency in pi units');
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      %In order to clearly see the relationship between DTFT and DFT, we draw DTFT on the same picture.
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      %Discrete-time Fourier Transform
     
    
   

    

     

    
    

     

      K = 500;
     
    
   

    

     

    
    

     

      k = 0:1:K;
     
    
   

    

     

    
    

     

      w = 2*pi*k/K; %plot DTFT in [0,2pi];
     
    
   

    

     

    
    

     

      X = x*exp(-j*n'*w);
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      magX = abs(X);
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      hold on 
     
    
   

    

     

    
    

     

      plot(w/pi,magX);
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      hold off
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
  
 

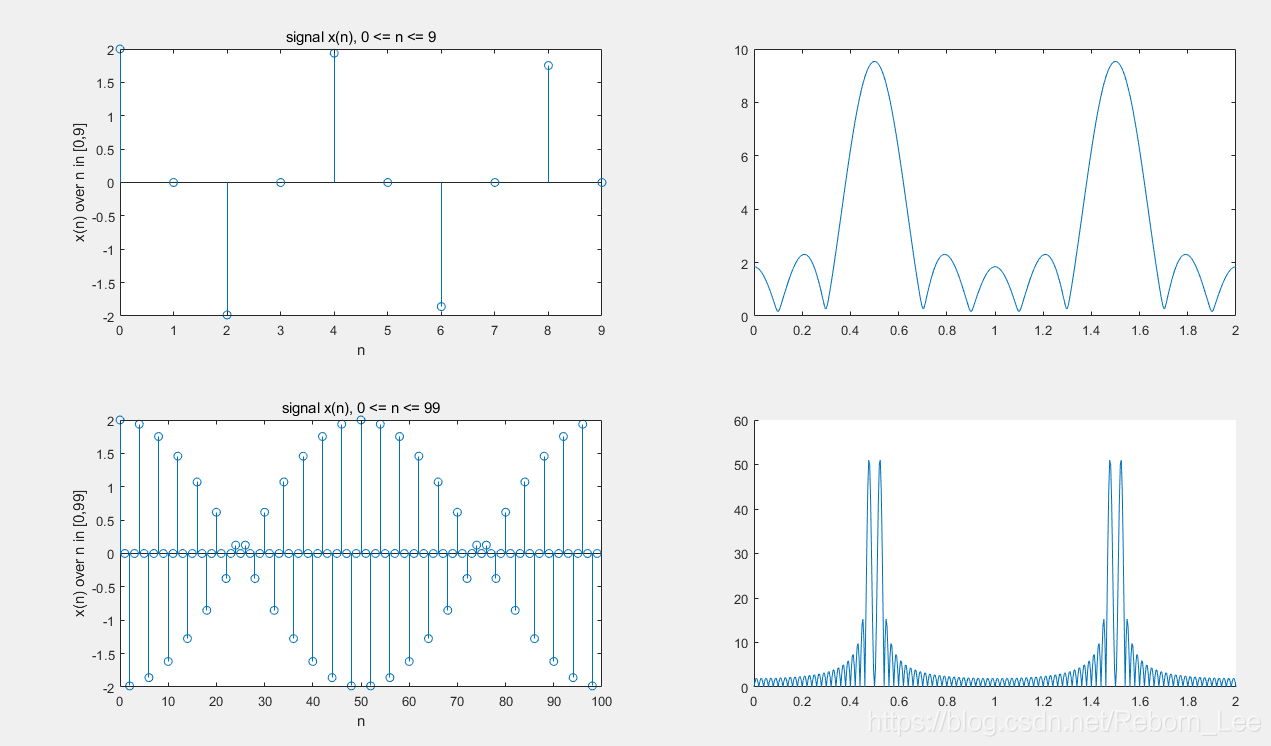
可见，b问这种情况，拥有x(n)的更多数据，所以得到的DTFT更加的准确，正如我们所料，频谱在w = 0.48pi以及0.52pi处取得峰值。而a问中的图就看不出这种关系，因为获得序列数据太少，已经严重影响到了频谱的形状。

文章来源: reborn.blog.csdn.net，作者：李锐博恩，版权归原作者所有，如需转载，请联系作者。

原文链接：reborn.blog.csdn.net/article/details/83478545