【 MATLAB 】DFT性质讨论(一)线性、循环反转、共轭与实序列的对称性的MATLAB实现
【摘要】 上篇博文通过在理论上讨论了DFT的三个性质:【 MATLAB 】DFT性质讨论(一)线性、循环反转与共轭
分别讨论:
一、线性
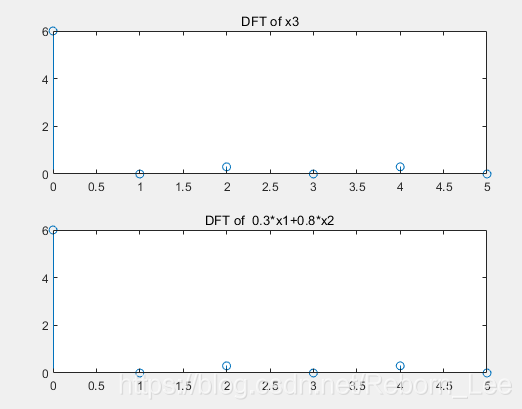
给出一个例子,给出x1和x2,x3 = 0.3*x1+0.8*x2;
之后我们求x3的DFT,和x1和x2的DFT的线性组合是否一致,即可验证线性性质。
clc,clear,close all; %signal 1n1 = 0:3;x1 =...
上篇博文通过在理论上讨论了DFT的三个性质:【 MATLAB 】DFT性质讨论(一)线性、循环反转与共轭
分别讨论:
一、线性
给出一个例子,给出x1和x2,x3 = 0.3*x1+0.8*x2;
之后我们求x3的DFT,和x1和x2的DFT的线性组合是否一致,即可验证线性性质。
-
clc,clear,close all;
-
-
%signal 1
-
n1 = 0:3;
-
x1 = [1,1,1,1];
-
-
%signal 2
-
n2 = 0:5;
-
x2 = ones(1,6);
-
-
% signal 3 = signal 1 +signal 2
-
n3 = 0:max(length(n1),length(n2))-1;
-
% modify x1 and x2
-
x1 = [ones(1,4),zeros(1,length(n3)-4)];
-
x2 = [ones(1,6),zeros(1,length(n3)-6)];
-
-
x3 = 0.3*x1+0.8*x2;
-
-
N = length(n3);
-
-
% DFT of x1
-
X1 = dft(x1,N);
-
-
% DFT of x2
-
X2 = dft(x2,N);
-
-
% DFT of x3
-
X3 = dft(x3,N);
-
-
% Linear property
-
X3_l = 0.3*X1 + 0.8*X2;
-
-
subplot(2,1,1);
-
stem(n3,X3);
-
title('DFT of x3');
-
-
subplot(2,1,2);
-
stem(n3,X3_l);
-
title('DFT of 0.3*x1+0.8*x2');
-
二、循环反转
给出例子:
设
求:
a. 求出并画出 
b. 验证循环反转性质。
题解:
a
-
clc,clear,close all;
-
-
n = 0:10;
-
x = 10 * (0.8).^n;
-
N = 11;
-
-
y = x( mod(-n,N)+1 );
-
-
subplot(2,1,1)
-
stem(n,x);
-
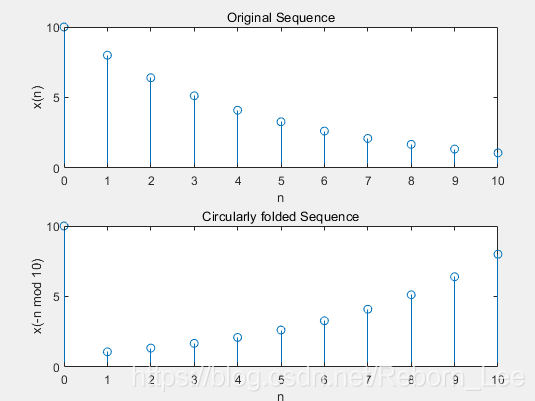
title('Original Sequence');
-
xlabel('n');ylabel('x(n)');
-
-
subplot(2,1,2)
-
stem(n,y);
-
title('Circularly folded Sequence');
-
xlabel('n');ylabel('x(-n mod 10)');
b
-
clc,clear,close all;
-
-
n = 0:10;
-
x = 10 * (0.8).^n;
-
N = 11;
-
-
y = x( mod(-n,N)+1 );
-
-
% subplot(2,1,1)
-
% stem(n,x);
-
% title('Original Sequence');
-
% xlabel('n');ylabel('x(n)');
-
%
-
% subplot(2,1,2)
-
% stem(n,y);
-
% title('Circularly folded Sequence');
-
% xlabel('n');ylabel('x(-n mod 10)');
-
k = n;
-
X = dft(x,N);
-
Y = dft(y,N);
-
RealX = real(X);
-
ImagX = imag(X);
-
-
RealY = real(Y);
-
ImagY = imag(Y);
-
-
subplot(2,2,1);
-
stem(k,RealX);
-
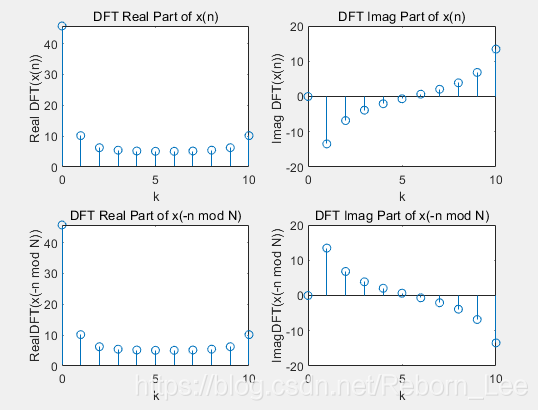
title('DFT Real Part of x(n)');
-
xlabel('k');ylabel('Real{ DFT(x(n)) }');
-
-
subplot(2,2,2);
-
stem(k,ImagX);
-
title('DFT Imag Part of x(n)');
-
xlabel('k');ylabel('Imag{ DFT(x(n)) }');
-
-
subplot(2,2,3);
-
stem(k,RealY);
-
title('DFT Real Part of x(-n mod N)');
-
xlabel('k');ylabel('Real{DFT(x(-n mod N))}');
-
-
subplot(2,2,4);
-
stem(k,ImagY);
-
title('DFT Imag Part of x(-n mod N)');
-
xlabel('k');ylabel('Imag{DFT(x(-n mod N))}');
三、共轭与时序列的对称性
我们讨论时序列的对称性,采用的例子是这篇博文中的:【 MATLAB 】模拟信号采样及离散时间傅里叶变换(DTFT)案例分析
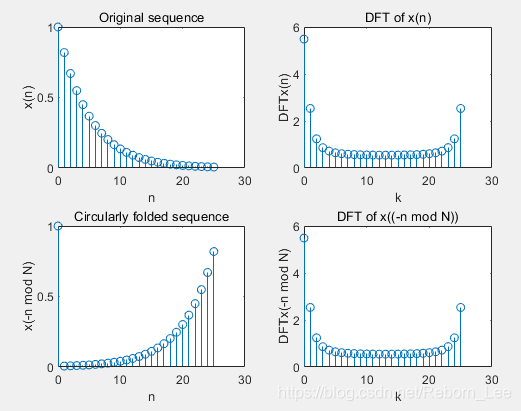
使用的模拟信号:

在 fs = 5000 对信号进行采样,可以得到离散时间序列。
之后讨论它的循环共轭对称性。
-
clc
-
clear
-
close all
-
-
-
% Discrete-time signal
-
Ts = 0.0002;
-
n = 0:25;
-
x = exp(-1000*abs(n*Ts));
-
N = length(n);
-
-
x1 = x( mod(-n,N) + 1 );
-
-
% DFT of x
-
X = dft(x,N);
-
-
X1 = dft(x1,N);
-
-
X1_c = conj(X1);
-
-
subplot(2,2,1);
-
stem(n,x);
-
title('Original sequence');
-
xlabel('n');ylabel('x(n)');
-
-
subplot(2,2,2);
-
stem(n,X);
-
title('DFT of x(n)');
-
xlabel('k');ylabel('DFT{x(n)}');
-
-
subplot(2,2,3);
-
stem(n,x1);
-
title('Circularly folded sequence');
-
xlabel('n');ylabel('x(-n mod N)');
-
-
subplot(2,2,4)
-
stem(n,X1);
-
title('DFT of x((-n mod N))');
-
xlabel('k');ylabel('DFT{x(-n mod N)}');
-
-
-
figure
-
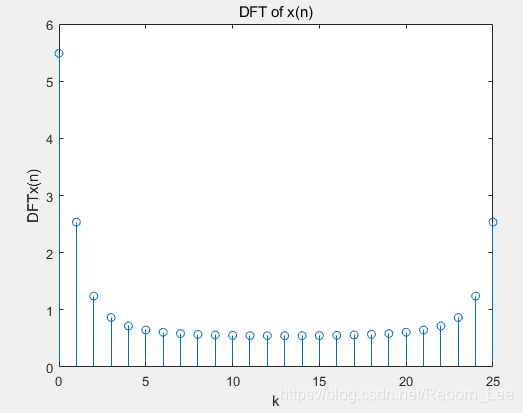
stem(n,X);
-
title('DFT of x(n)');
-
xlabel('k');ylabel('DFT{x(n)}');
-
-
-
figure
-
-
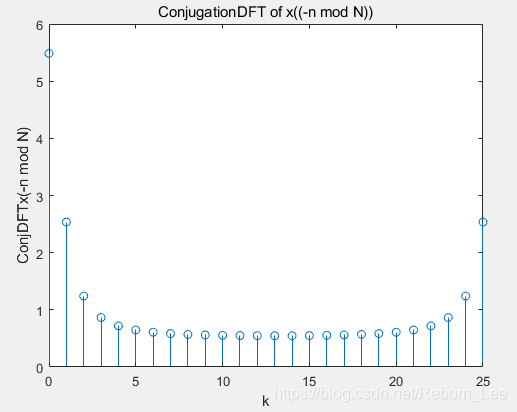
stem(n,X1_c);
-
title('Conjugation{DFT of x((-n mod N))}');
-
xlabel('k');ylabel('Conj{DFT{x(-n mod N)}}');
-
-
-
-
-
-
文章来源: reborn.blog.csdn.net,作者:李锐博恩,版权归原作者所有,如需转载,请联系作者。
原文链接:reborn.blog.csdn.net/article/details/83507287
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)