【 Notes 】TOA Measurement Model
TOA is the one - way propagation time of the signal traveling between a source and a receiver. This implies that the target and all receivers are required to be precisely synchronized to obtain the TOA information, although such synchronization is not needed if the round - trip or two - way TOA is measured. Multiplying the TOAs by the known propagation speed, denoted by c , provides the distances between the source and receivers. For example,  are the speeds of sound and light, respectively, in the in - air scenarios.
are the speeds of sound and light, respectively, in the in - air scenarios.
In the absence of measurement error, each TOA corresponds to a circle centered at a receiver on which the source must lie in the 2 - D space. As discussed in Chapter 1 , geometrically, three or more circles deduced from the noise - free TOAs will result in a unique intersection, which is the source position, implying that at least three sensors are needed for 2 - D positioning.
TOA 是信号单向传播的时间,这就要求目标和接受者之间时钟精确同步,因为电磁波传播速度很快,很小的时间误差就可以导致很大的距离误差,如果测量往返或双向TOA,则不需要这种同步。
由测量得到的信号到达时间,乘以已知的速度,就可以得到距离。
如果不考虑测量误差,在二维平面中,每个TOA对应于一个圆,圆心位于测量站。在几何上,三个或者更多的圆可以确定一个交叉点,这个交叉点就是目标位置,这就意味着,在二维平面中,使用TOA定位,则至少需要三个测量站。
Note that two TOA circles generally have two intersection points, which correspond to two possible source locations. Nevertheless, these circles may not intersect or have multiple intersections in the presence of disturbance, and hence it is not an effective way to solve the problem using the circles directly. In fact, with three or more receivers, it is more appropriate to convert the noisy TOAs into a set of circular equations from which the source position can be determined according to an optimization criterion, with the knowledge of the sensor array geometry.
注意,两个TOA圆通常具有两个交叉点,其对应于两个可能的源位置。 然而,在存在干扰的情况下,这些圆可能不交叉或具有多个交叉点,因此不是直接使用圆来解决问题的有效方式。 实际上,对于三个或更多个接收器,更有利的是将噪声TOA转换成一组圆形方程,根据优化标准可以根据传感器阵列几何形状确定源位置。
Mathematically, the TOA measurement model is formulated as follows.
Let ![\bold x = [x,y]^T](https://res-hd.hc-cdn.cn/ecology/9.3.204/v2_resources/ydcomm/libs/images/loading.gif) be the unknown source position and
be the unknown source position and ![\bold x_l = [x_l,y_l]^T](https://res-hd.hc-cdn.cn/ecology/9.3.204/v2_resources/ydcomm/libs/images/loading.gif) be the known coordinates of the l th sensor, l = 1, 2, … , L , where L ≥ 3 is the number of receivers. The distance between the source and the l th sensor, denoted by , is simply
be the known coordinates of the l th sensor, l = 1, 2, … , L , where L ≥ 3 is the number of receivers. The distance between the source and the l th sensor, denoted by , is simply
 (1)
(1)
Without loss of generality, we assume that the source emits a signal at time 0 and the l th sensor receives it at time t l ; that is, { t l } are the TOAs and we have a simple relationship between t l and d l :
 (2)
(2)
如果不考虑测量误差,那么上面两个式子联立就可以得到一个圆的方程。
In practice, TOAs are subject to measurement errors. As a result, the range measurement based on multiplying t l by c , denoted by , is modeled as:
, is modeled as:
 (3)
(3)
where  is the range error in
is the range error in  , which results from the TOA disturbance.
, which results from the TOA disturbance.
(3)式用向量的形式表示如下:
 (4)
(4)
其中,
![\bold{r_{TOA}}= [r_{TOA,1},r_{TOA,2},...,r_{TOA,L}]^T](https://res-hd.hc-cdn.cn/ecology/9.3.204/v2_resources/ydcomm/libs/images/loading.gif) (5)
(5)
![\bold{n_{TOA}}= [n_{TOA,1},n_{TOA,2},...,n_{TOA,L}]^T](https://res-hd.hc-cdn.cn/ecology/9.3.204/v2_resources/ydcomm/libs/images/loading.gif) (6)
(6)
 (7)
(7)
Here, represents the known function, which is parameterized by x , and in fact, it is the noise - free distance vector. The source localization problem based on TOA measurements is to estimate x given
represents the known function, which is parameterized by x , and in fact, it is the noise - free distance vector. The source localization problem based on TOA measurements is to estimate x given  .
.
To facilitate the algorithm development and analysis as well as the CRLB computation, it is assumed that {  } are zero - mean uncorrelated Gaussian processes with variances
} are zero - mean uncorrelated Gaussian processes with variances  . It is noteworthy that the zero - mean property indicates LOS transmission.
. It is noteworthy that the zero - mean property indicates LOS transmission.
值得注意的是,零均值属性表明LOS传输。
The probability density function ( PDF ) for each scalar random variable , denoted by
, denoted by , has the form of:
, has the form of:
 (8)
(8)
which is characterized by its mean and variance,  and
and  ,respectively.
,respectively.
In other words, we can write  .
.
The PDF for  , denoted by p (
, denoted by p (  ), is
), is
 (9)
(9)
where  is the covariance matrix for
is the covariance matrix for  , which corresponds to
, which corresponds to
 (10)
(10)
In Equation 10, the third equality is deduced using the assumption of uncorrelated { n TOA, l }.
(9) (10)联立,得:
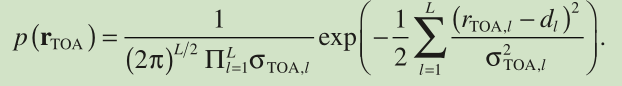 (11)
(11)
In other words, we can write
![]()
文章来源: reborn.blog.csdn.net,作者:李锐博恩,版权归原作者所有,如需转载,请联系作者。
原文链接:reborn.blog.csdn.net/article/details/84106016
- 点赞
- 收藏
- 关注作者


评论(0)