【 Notes 】ML ALGORITHMS of TOA - Based Positioning
这篇博文和NLS方法博文行文思路类似:【 Notes 】NLS ALGORITHMS of TOA - Based Positioning
ML方法是NLS方法的一个推广版本,具体接着看:
Assuming that the error distribution is known, the ML approach maximizes the PDFs of TOA measurements to obtain the source location. When the disturbances in the measurements are zero - mean Gaussian distributed, it is shown in the following that maximization of Equations 1 will correspond to a weighted version of the NLS scheme.
第  个
个 的PDF:
的PDF:

向量形式:
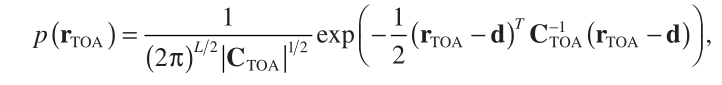 (1)
(1)
the covariance matrix for 


![]()
To facilitate the maximization of Equation (1) , we consider its logarithmic version:
 (2)
(2)
As the first term is independent of x , maximizing Equation (2) is in fact equivalent to minimizing the second term, the ML estimate is
 (3)
(3)
or we can write
 (4)
(4)
where  denotes the ML cost function for TOA - based positioning, which has the form of
denotes the ML cost function for TOA - based positioning, which has the form of
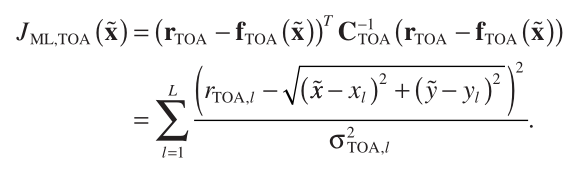 (5)
(5)
Comparing Equations (4) and (5) , it is observed that in the presence of zero - mean Gaussian noise, the ML estimator generalizes the NLS method because the former is a weighted version of the latter.
比较等式(4)和(5),观察到在存在零均值高斯噪声的情况下,ML估计器推广了NLS方法,因为前者是后者的加权版本。
Intuitively speaking, when  is large, which corresponds to a large noise in
is large, which corresponds to a large noise in , a small weight of
, a small weight of  is employed in the squared term of
is employed in the squared term of

and vice versa.
When  is proportional to the identity matrix or
is proportional to the identity matrix or  are identical, the ML estimator is reduced to the NLS method. To compute Equation (4) , we can follow the numerical methods discussed in the NLS approach. In particular, the Newton – Raphson procedure for Equation (4) is
are identical, the ML estimator is reduced to the NLS method. To compute Equation (4) , we can follow the numerical methods discussed in the NLS approach. In particular, the Newton – Raphson procedure for Equation (4) is
 (6)
(6)
 (7)
(7)
 (8)
(8)
 (9)
(9)
 (10)
(10)
 (11)
(11)
On the other hand, the corresponding Gauss – Newton and steepest descent algorithms are, respectively,
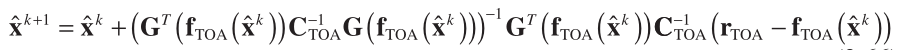 (12)
(12)
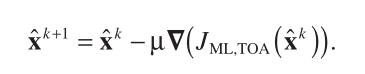 (13)
(13)
下面的博文,将对这三种方法进行TOA定位仿真。
文章来源: reborn.blog.csdn.net,作者:李锐博恩,版权归原作者所有,如需转载,请联系作者。
原文链接:reborn.blog.csdn.net/article/details/84140774
- 点赞
- 收藏
- 关注作者


评论(0)