【 LLS 】Linear Approaches of TOA - Based Positioning
Linear Approaches
The basic idea of the linear localization methodology is to convert the nonlinear expressions of Equations (1) into a set of linear equations with zero - mean disturbances, assuming that the measurement errors are sufficiently small.
线性定位方法的基本思想是将等式(1)的非线性表达式转换为一组具有零均值扰动的线性方程,假设测量误差足够小。
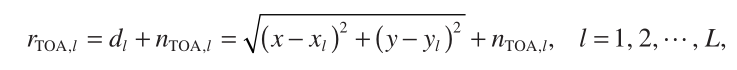 (1)
(1)
As the corresponding optimization cost functions are now unimodal, it is always guaranteed to obtain the global solution. Three linear positioning approaches, namely, LLS, WLLS, and subspace estimators, will be presented as follows.
由于相应的优化成本函数现在是单峰的,因此始终保证获得全局解决方案。 三种线性定位方法,即LLS,WLLS和子空间估计器将如下呈现。
Analogous to NLS and ML estimators, the WLLS method is a weighted version of the LLS scheme and it provides higher localization accuracy, although the mean and covariance of the errors in the linear equations are required for the weight computation. On the other hand, the subspace technique fi rst relates x with the squared pairwise distances among the source and receivers. Source localization is
then achieved using an eigenvalue decomposition ( EVD ) procedure.
类似于NLS和ML估计器,WLLS方法是LLS方案的加权版本,并且它提供更高的定位精度,尽管线性方程中的误差的均值和协方差是权重计算所需的。 另一方面,子空间技术首先将x与源和接收器之间的平方成对距离相关联。 然后使用特征值分解(EVD)过程实现源定位。
LLS
The LLS approach attempts to reorganize Equations (1) into linear equations in x , and the position is then estimated by using the ordinary LS technique. For TOA, TDOA, and RSS measurements, we have to introduce an intermediate variable, which is a function of the source position in the linearization process. The LLS location estimators based on TOA, TDOA, RSS, and DOA information are developed one by one as follows.
LLS方法试图将方程(1)重组为x中的线性方程,然后使用普通LS技术估计位置。 对于 TOA 测量,我们必须引入一个中间变量,它是线性化过程中源位置的函数。 基于 TOA 信息的LLS位置估计器如下。
TOA - Based Positioning
To convert the TOA measurements into linear models in x , we first consider squaring both sides of Equation (1) to obtain
![]() (2)
(2)
Let
 (3)
(3)
be the noise component in Equation (2) and introduce a dummy variable R of the form
是等式(2)中的噪声分量,并引入形式的虚拟变量R.
![]() (4)
(4)
Substituting Equations (3) and (4) into (2) yields
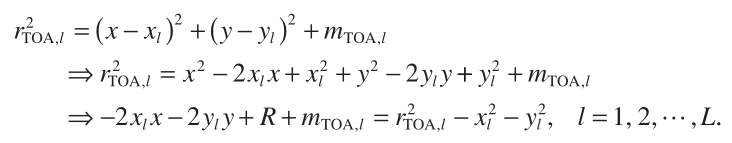 (5)
(5)
Let
 (6)
(6)
 (7)
(7)
 (8)
(8)
and
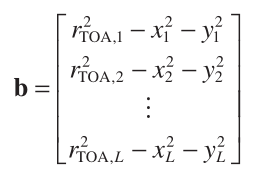 (9)
(9)
The matrix form for Equation (5) is then
![]() (10)
(10)
where the observed  of Equation
of Equation
 (11)
(11)
is now transformed to b , A is constructed from the known receiver positions, and θ contains the source location to be determined. When  are sufficiently small such that
are sufficiently small such that
 现在转换为 b,A 由已知的接收器位置构成,θ 包含要确定的源位置。当
现在转换为 b,A 由已知的接收器位置构成,θ 包含要确定的源位置。当  足够小
足够小
 (12)
(12)
can be considered a zero - mean vector; that is, E { q } ≈ 0 , we can approximate Equation (11)as
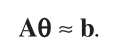 (13)
(13)
the LS cost function based on Equation (13) is
 (14)
(14)
which is a quadratic function in  , indicating that there is a unique minimum in
, indicating that there is a unique minimum in  .
.
The LLS estimate corresponds to
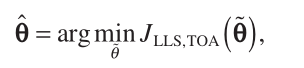 (15)
(15)
which can be easily computed by differentiating Equation (14) with respect to  and by setting the resultant expression to zero:
and by setting the resultant expression to zero:
 (16)
(16)
The LLS position estimate is simply extracted from the fi rst and second entries of  ; that is,
; that is,
 (17)
(17)
In the literature, Equation (17) is also referred to as the LS calibration method .
在文献中,等式(17)也称为LS校准方法。
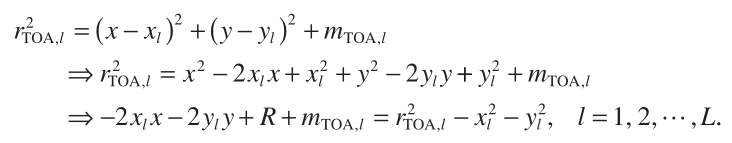 (5)
(5)
An alternative way for LLS TOA - based positioning is to eliminate R in Equation (5) by employing the differences between any two equations [18] . For simplicity but without loss of generality, subtracting the first equation of Equation (5) from the remaining ( L − 1) equations, R is removed and we have
 (18)
(18)
or in matrix form
![]() (19)
(19)
where A , q , and b are now modifi ed to
 (20)
(20)
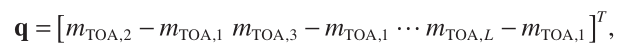 (21)
(21)
 (22)
(22)
Assuming sufficiently small noise conditions and following Equations (12)——(16), a variant of the LLS method using TOA measurements is
![]() (23)
(23)
文章来源: reborn.blog.csdn.net,作者:李锐博恩,版权归原作者所有,如需转载,请联系作者。
原文链接:reborn.blog.csdn.net/article/details/84146235
- 点赞
- 收藏
- 关注作者


评论(0)