【 FPGA 】特定情况下消除不稳定态的方法
不是没有方法,但方法也不多,最典型的就是使用格雷码。
消除不稳定态的原理
通过上篇博文:https://blog.csdn.net/Reborn_Lee/article/details/84439777
通过对多触发器寄存器的分析,我们知道了产生不稳定态的原因,那就是组成寄存器的各个触发器输出变化时刻的客观不一致性。(我们希望各个触发器输出变化时刻一致)。因此,要想消除不稳定态,就必须消除多触发器输出变化时刻的不一致才行。可触发器不可能完全一致,更没有精确等长的物理连线,所以想要协调一致多个触发器的输出变化时刻来消除寄存器输出的不稳定态, 几乎是不可能的。
此路不通,换个思路。
如果能让寄存器中的各个触发器每次只有一个输出会发生变化,那么自然就不存在变化时刻不一致的问题了,从而从根本上杜绝了不稳定态的产生。
格雷码简介
格雷码是一种数字排序系统,其中的所有相邻整数在它们的二进制表示中仅有一位不同。
下表给出了4bit自然二进制码、格雷码与十进制整数的对照表:
| 十进制数 | 4位自然二进制码 | 4位典型格雷码 |
|---|---|---|
| 0 |
0000 |
0000 |
| 1 |
0001 |
0001 |
| 2 |
0010 |
0011 |
| 3 |
0011 |
0010 |
| 4 |
0100 |
0110 |
| 5 |
0101 |
0111 |
| 6 |
0110 |
0101 |
| 7 |
0111 |
0100 |
| 8 |
1000 |
1100 |
| 9 |
1001 |
1101 |
| 10 |
1010 |
1111 |
| 11 |
1011 |
1110 |
| 12 |
1100 |
1010 |
| 13 |
1101 |
1011 |
| 14 |
1110 |
1001 |
| 15 |
1111 |
1000 |
从上表可以看出,格雷码在任意两个相邻的数之间转换时,只有1bit发生了变化,所以它有效地避免了寄存器从一个数值到下一个数值时的不稳定态。
由于格雷码中最大数和最小数之间也仅有1bit不同,所以又称为循环二进制码,或者反射二进制码。
常用的格雷码编解码方法
1从自然二进制码到格雷码:该过程又称为格雷码的编码。
方法是从二进制码的最右边一位(最低位)起,依次将每一位与左边一位进行异或运算,作为对应格雷码该位的值,而最左边一位(最高位)不变。对应的公式为:
![g[n] = b[n]](https://res-hd.hc-cdn.cn/ecology/9.3.204/v2_resources/ydcomm/libs/images/loading.gif)
![g[i]=b[i]xorb[i+1](i\in N,n-1\geqi \geq0)](https://res-hd.hc-cdn.cn/ecology/9.3.204/v2_resources/ydcomm/libs/images/loading.gif)
例:

根据上面的公式很容易写出二进制码转换为格雷码的程序:(Verilog HDL)
-
module bin_to_gray(
-
-
bin_in,
-
-
gray_out
-
-
);
-
-
parameter data_width = 4;
-
-
-
-
input [data_width-1:0] bin_in;
-
-
output [data_width-1:0] gray_out;
-
-
-
-
assign gray_out = (bin_in >> 1) ^ bin_in;
-
-
-
-
endmodule
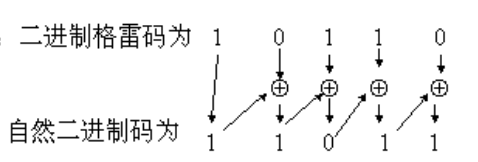
2 从格雷码到二进制码:该过程又叫格雷码的解码,方法是从格雷码左边第二位(次高位)起,将每一位与其左边一位解码后的值异或,作为该位解码后的值,而最高位的解码结果是其本身。对应公式如下:
![b[n]=g[n]](https://res-hd.hc-cdn.cn/ecology/9.3.204/v2_resources/ydcomm/libs/images/loading.gif)
![b[i]= g[i]xorb[i+1] (i \in N,n-1\geq i \geq 0)](https://res-hd.hc-cdn.cn/ecology/9.3.204/v2_resources/ydcomm/libs/images/loading.gif)
例:
根据上面的公式,很容易编写出转换程序:(Verilog HDL)
-
module gray_to_bin(
-
-
gray_in,
-
-
bin_out
-
-
);
-
-
parameter data_width = 4;
-
-
-
-
input [data_width-1:0] gray_in;
-
-
output [data_width-1:0] bin_out;
-
-
reg [data_width-1:0] bin_out;
-
-
always @(gray_in)
-
-
begin
-
-
bin_out[3] = gray_in[3];
-
-
bin_out[2] = gray_in[2]^bin_out[3];
-
-
bin_out[1] = gray_in[1]^bin_out[2];
-
-
bin_out[0] = gray_in[0]^bin_out[1];
-
-
end
-
-
endmodule
参考:
FPGA之道
文章来源: reborn.blog.csdn.net,作者:李锐博恩,版权归原作者所有,如需转载,请联系作者。
原文链接:reborn.blog.csdn.net/article/details/84441388
- 点赞
- 收藏
- 关注作者


评论(0)