移动机器人中的现代控制理论之状态空间表达式

状态空间表达式一般是现代控制理论的第一章，关于课程可以详细查看：

https://zhangrelay.blog.csdn.net/article/category/6161998

所有课程相关资料链接如下：

https://zhangrelay.blog.csdn.net/article/details/51195007

在讲述课程时，发现部分学生对于状态空间模型概念并没有非常形象的认知，机械的记忆公式，从而失去学习课程的乐趣，探索控制理论的热情。其实，现代控制理论非常简单，整本书都围绕如下这个公式展开：

然后，一般而言，教材会有R-L-C电路或者带弹簧阻尼的机械运动模型，刷一波上述公式，嗯，没办法都是这样的。

放个图，大家感受一下：

 然后，经过一系列推导，得到如下公式：

对应公式：

想要了解更多信息，参考如下链接：

http://www.mbstudent.com/control-theory-state-space-representation-RLC-circuit-example-1.html

但是，不生动不形象啊~讲的人痛苦，听的人无趣。索性换一个例子吧：

两轮差动模型的机器人仿真环境

上图中有两个机器人，相对坐标系等先不讲，此处只关注单个机器人在地面上的运动特性。

机器人左轮和右轮的运动使得机器人在环境空间状态发生变化。大部分低成本平地两轮机器人都是类似的模型，如扫地机器人，巡逻机器人等。

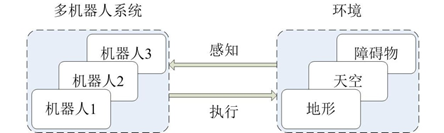输入----系统----输出（机器人与环境交互）

具体公式推导，可以参考：

http://planning.cs.uiuc.edu/node659.html

更具体过程稍后补充：

第一种（全局坐标系）：

第二种（机器人坐标系）：

上述图片为引用。

这时候会发现？说好的状态空间模型怎么不对劲呢？？？只有：

这是分割线

思考一下，机器人难道没有惯性吗？当停止电机供电，机器人是立刻停止，还是需要滑行一小段距离？

上述模型是运动学模型，是经过简化的，更真实的模型如下：

其中：

各变量具体含义：

Iv 机器人重心的转动惯量 Moment of inertia around the C.G. of robot

M 机器人质量 Mass of the robot

l 左右轮与机器人重心之间的距离 Distance between left and right wheel and the c.g. of robot

Iw 车轮转动惯量 Moment of inertia of wheel

c 粘滞摩擦系数 Viscous friction factor

r 车轮半径 Radius of wheel

k 驱动增益系数 Driving gain factor

思考：为何A为系统矩阵，B为控制（输入）矩阵，C为输出（感知）矩阵？

此文目前为草稿，待后续完善。

文章来源: zhangrelay.blog.csdn.net，作者：zhangrelay，版权归原作者所有，如需转载，请联系作者。

原文链接：zhangrelay.blog.csdn.net/article/details/88033016