强化学习笔记3-Python/OpenAI/TensorFlow/ROS-规划博弈

规划：主要涉及马尔科夫决策（MDP），常用于已知环境求解；

博弈：主要涉及蒙特卡罗方法，常用于未知状态求解。

• 基础知识点：
• Markov Decision Processes-MIT
• https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-825-techniques-in-artificial-intelligence-sma-5504-fall-2002/lecture-notes/Lecture20FinalPart1.pdf
• Markov Decision Processes-Harvard
• http://am121.seas.harvard.edu/site/wp-content/uploads/2011/03/MarkovDecisionProcesses-HillierLieberman.pdf
• Markov Decision Processes-Purdue&Duke
• https://www.cs.rice.edu/~vardi/dag01/givan1.pdf
• Monte Carlo Method-MIT
• http://web.mit.edu/course/16/16.90/BackUp/www/pdfs/Chapter17.pdf
• http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching_files

案例分析：

利用价值迭代解决冻湖问题
目标：
想象一下，从你家到办公室有一个冰冻的湖泊，你应该在冰冻的湖面上走到你的办公室。 但是哎呀！ 在它们之间的冰冻湖中会有一个洞，因此在冰冻的湖中行走时要小心，以免被困在洞中。 看下图，其中：

S是起始位置（家）
F是可以步行的冰湖
H是必须非常小心的洞
G是目标（办公室）

好的，现在让我们使用我们的智能体而不是您来找到到达办公室的正确方法。 智能体的目标是找到从S到G的最佳路径，而不会被困在H.如何代理可以实现这一目标？ 如果它正确地在冰冻的湖面上行走，我们给予代理+1点作为奖励，如果它落入洞中则给0点。 因此，智能体可以确定哪个是正确的操作。 智能体现在将尝试找到最优策略。 最优政策意味着采取最大化智能体奖励的正确途径。 如果智能体正在最大化奖励，显然智能体正在学习跳过洞并到达目的地。

具体实现代码如下：

  

   

    

     

    
    

     

      import gym
     
    
   

    

     

    
    

     

      import numpy as np
     
    
   

    

     

    
    

     

      env = gym.make('FrozenLake-v0')
     
    
   

    

     

    
    

     

      env.render()
     
    
   

    

     

    
    

     

      def value_iteration(env, gamma = 1.0):
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # initialize value table with zeros
     
    
   

    

     

    
    

     

       value_table = np.zeros(env.observation_space.n)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # set number of iterations and threshold
     
    
   

    

     

    
    

     

       no_of_iterations = 100000
     
    
   

    

     

    
    

     

       threshold = 1e-20
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 for i in range(no_of_iterations):
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # On each iteration, copy the value table to the updated_value_table
     
    
   

    

     

    
    

     

       updated_value_table = np.copy(value_table) 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # Now we calculate Q Value for each actions in the state 
     
    
   

    

     

    
    

     
 # and update the value of a state with maximum Q value
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 for state in range(env.observation_space.n):
     
    
   

    

     

    
    

     

       Q_value = []
     
    
   

    

     

    
    

     
 for action in range(env.action_space.n):
     
    
   

    

     

    
    

     

       next_states_rewards = []
     
    
   

    

     

    
    

     
 for next_sr in env.env.P[state][action]: 
     
    
   

    

     

    
    

     

       trans_prob, next_state, reward_prob, _ = next_sr 
     
    
   

    

     

    
    

     

       next_states_rewards.append((trans_prob * (reward_prob + gamma * updated_value_table[next_state]))) 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

       Q_value.append(np.sum(next_states_rewards))
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

       value_table[state] = max(Q_value) 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # we will check whether we have reached the convergence i.e whether the difference 
     
    
   

    

     

    
    

     
 # between our value table and updated value table is very small. But how do we know it is very
     
    
   

    

     

    
    

     
 # small? We set some threshold and then we will see if the difference is less
     
    
   

    

     

    
    

     
 # than our threshold, if it is less, we break the loop and return the value function as optimal
     
    
   

    

     

    
    

     
 # value function
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 if (np.sum(np.fabs(updated_value_table - value_table)) <= threshold):
     
    
   

    

     

    
    

     
 print ('Value-iteration converged at iteration# %d.' %(i+1))
     
    
   

    

     

    
    

     
 break
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 return value_table
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      def extract_policy(value_table, gamma = 1.0):
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # initialize the policy with zeros
     
    
   

    

     

    
    

     

       policy = np.zeros(env.observation_space.n) 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 for state in range(env.observation_space.n):
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # initialize the Q table for a state
     
    
   

    

     

    
    

     

       Q_table = np.zeros(env.action_space.n)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # compute Q value for all ations in the state
     
    
   

    

     

    
    

     
 for action in range(env.action_space.n):
     
    
   

    

     

    
    

     
 for next_sr in env.env.P[state][action]: 
     
    
   

    

     

    
    

     

       trans_prob, next_state, reward_prob, _ = next_sr 
     
    
   

    

     

    
    

     

       Q_table[action] += (trans_prob * (reward_prob + gamma * value_table[next_state]))
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # select the action which has maximum Q value as an optimal action of the state
     
    
   

    

     

    
    

     

       policy[state] = np.argmax(Q_table)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 return policy
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      optimal_value_function = value_iteration(env=env,gamma=1.0)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      optimal_policy = extract_policy(optimal_value_function, gamma=1.0)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      print(optimal_value_function)
     
    
   

    

     

    
    

     

      print(optimal_policy)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
  
 

显示结果如下：

SFFF
FHFH
FFFH
HFFG
Value-iteration converged at iteration# 1373.
[0.82352941 0.82352941 0.82352941 0.82352941

0.82352941 0.  0.52941176 0.        

0.82352941 0.82352941 0.76470588 0.
 0.         0.88235294 0.94117647 0.        ]
[0. 3. 3. 3. 0. 0. 0. 0. 3. 1. 0. 0. 0. 2. 1. 0.]

使用策略迭代解决冻湖问题

具体实现代码如下：

  

   

    

     

    
    

     

      import gym
     
    
   

    

     

    
    

     

      import numpy as np
     
    
   

    

     

    
    

     

      env = gym.make('FrozenLake-v0')
     
    
   

    

     

    
    

     

      env.render()
     
    
   

    

     

    
    

     

      def compute_value_function(policy, gamma=1.0):
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # initialize value table with zeros
     
    
   

    

     

    
    

     

       value_table = np.zeros(env.env.nS)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # set the threshold
     
    
   

    

     

    
    

     

       threshold = 1e-10
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 while True:
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # copy the value table to the updated_value_table
     
    
   

    

     

    
    

     

       updated_value_table = np.copy(value_table)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # for each state in the environment, select the action according to the policy and compute the value table
     
    
   

    

     

    
    

     
 for state in range(env.env.nS):
     
    
   

    

     

    
    

     

       action = policy[state]
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # build the value table with the selected action
     
    
   

    

     

    
    

     

       value_table[state] = sum([trans_prob * (reward_prob + gamma * updated_value_table[next_state]) 
     
    
   

    

     

    
    

     
 for trans_prob, next_state, reward_prob, _ in env.env.P[state][action]])
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 if (np.sum((np.fabs(updated_value_table - value_table))) <= threshold):
     
    
   

    

     

    
    

     
 break
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 return value_table
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      def extract_policy(value_table, gamma = 1.0):
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # Initialize the policy with zeros
     
    
   

    

     

    
    

     

       policy = np.zeros(env.observation_space.n) 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 for state in range(env.observation_space.n):
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # initialize the Q table for a state
     
    
   

    

     

    
    

     

       Q_table = np.zeros(env.action_space.n)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # compute Q value for all ations in the state
     
    
   

    

     

    
    

     
 for action in range(env.action_space.n):
     
    
   

    

     

    
    

     
 for next_sr in env.env.P[state][action]: 
     
    
   

    

     

    
    

     

       trans_prob, next_state, reward_prob, _ = next_sr 
     
    
   

    

     

    
    

     

       Q_table[action] += (trans_prob * (reward_prob + gamma * value_table[next_state]))
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # Select the action which has maximum Q value as an optimal action of the state
     
    
   

    

     

    
    

     

       policy[state] = np.argmax(Q_table)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 return policy
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      def policy_iteration(env,gamma = 1.0):
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # Initialize policy with zeros
     
    
   

    

     

    
    

     

       old_policy = np.zeros(env.observation_space.n)   
     
    
   

    

     

    
    

     

       no_of_iterations = 200000
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 for i in range(no_of_iterations):
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # compute the value function
     
    
   

    

     

    
    

     

       new_value_function = compute_value_function(old_policy, gamma)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # Extract new policy from the computed value function
     
    
   

    

     

    
    

     

       new_policy = extract_policy(new_value_function, gamma)
     
    
   

    

     

    
    

     
   
     
    
   

    

     

    
    

     
 # Then we check whether we have reached convergence i.e whether we found the optimal
     
    
   

    

     

    
    

     
 # policy by comparing old_policy and new policy if it same we will break the iteration
     
    
   

    

     

    
    

     
 # else we update old_policy with new_policy
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 if (np.all(old_policy == new_policy)):
     
    
   

    

     

    
    

     
 print ('Policy-Iteration converged at step %d.' %(i+1))
     
    
   

    

     

    
    

     
 break
     
    
   

    

     

    
    

     

       old_policy = new_policy
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 return new_policy
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      print (policy_iteration(env))
     
    
  
 

显示结果如下：

SFFF
FHFH
FFFH
HFFG
Policy-Iteration converged at step 7.
[0. 3. 3. 3. 0. 0. 0. 0. 3. 1. 0. 0. 0. 2. 1. 0.]

思考：比较价值迭代和策略迭代的差异？

掌握：马尔科夫特征和应用，即时奖励和折扣系数，贝尔曼方程的作用，推导Q函数贝尔曼方程，值函数与Q函数关联性。

用蒙特卡罗估计的值

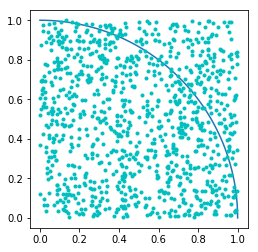
代码如下：

  

   

    

     

    
    

     

      import numpy as np
     
    
   

    

     

    
    

     

      import math
     
    
   

    

     

    
    

     

      import random
     
    
   

    

     

    
    

     

      import matplotlib.pyplot as plt
     
    
   

    

     

    
    

     

      #%matplotlib inline
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      square_size = 1
     
    
   

    

     

    
    

     

      points_inside_circle = 0
     
    
   

    

     

    
    

     

      points_inside_square = 0
     
    
   

    

     

    
    

     

      sample_size = 1000
     
    
   

    

     

    
    

     

      arc = np.linspace(0, np.pi/2, 100)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      def generate_points(size):
     
    
   

    

     

    
    

     

       x = random.random()*size
     
    
   

    

     

    
    

     

       y = random.random()*size
     
    
   

    

     

    
    

     
 return (x, y)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      def is_in_circle(point, size):
     
    
   

    

     

    
    

     
 return math.sqrt(point[0]**2 + point[1]**2) <= size
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      def compute_pi(points_inside_circle, points_inside_square):
     
    
   

    

     

    
    

     
 return 4 * (points_inside_circle / points_inside_square) 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      plt.axes().set_aspect('equal')
     
    
   

    

     

    
    

     

      plt.plot(1*np.cos(arc), 1*np.sin(arc))
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      for i in range(sample_size):
     
    
   

    

     

    
    

     

       point = generate_points(square_size)
     
    
   

    

     

    
    

     

       plt.plot(point[0], point[1], 'c.')
     
    
   

    

     

    
    

     

       points_inside_square += 1
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 if is_in_circle(point, square_size):
     
    
   

    

     

    
    

     

       points_inside_circle += 1
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      print("Approximate value of pi is {}"
     
    
   

    

     

    
    

     

      .format(compute_pi(points_inside_circle, points_inside_square)))
     
    
  
 

样本2000：

第一次
Approximate value of pi is 3.148
第二次
Approximate value of pi is 3.132
第三次
Approximate value of pi is 3.184

样本10000：

Approximate value of pi is 3.1444

BlackJack游戏

  

   

    

     

    
    

     

      import gym
     
    
   

    

     

    
    

     

      import numpy as np
     
    
   

    

     

    
    

     

      from matplotlib import pyplot
     
    
   

    

     

    
    

     

      import matplotlib.pyplot as plt
     
    
   

    

     

    
    

     

      from mpl_toolkits.mplot3d import Axes3D
     
    
   

    

     

    
    

     

      from collections import defaultdict
     
    
   

    

     

    
    

     

      from functools import partial
     
    
   

    

     

    
    

     

      %matplotlib inline
     
    
   

    

     

    
    

     

      plt.style.use('ggplot')
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      env = gym.make('Blackjack-v0')
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      def sample_policy(observation):
     
    
   

    

     

    
    

     

       score, dealer_score, usable_ace = observation
     
    
   

    

     

    
    

     
 return 0 if score >= 20 else 1
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      def generate_episode(policy, env):
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # we initialize the list for storing states, actions, and rewards
     
    
   

    

     

    
    

     

       states, actions, rewards = [], [], []
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # Initialize the gym environment
     
    
   

    

     

    
    

     

       observation = env.reset()
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 while True:
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # append the states to the states list
     
    
   

    

     

    
    

     

       states.append(observation)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # now, we select an action using our sample_policy function and append the action to actions list
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

       action = sample_policy(observation)
     
    
   

    

     

    
    

     

       actions.append(action)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # We perform the action in the environment according to our sample_policy, move to the next state 
     
    
   

    

     

    
    

     
 # and receive reward
     
    
   

    

     

    
    

     

       observation, reward, done, info = env.step(action)
     
    
   

    

     

    
    

     

       rewards.append(reward)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # Break if the state is a terminal state
     
    
   

    

     

    
    

     
 if done:
     
    
   

    

     

    
    

     
 break
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 return states, actions, rewards
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      def first_visit_mc_prediction(policy, env, n_episodes):
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # First, we initialize the empty value table as a dictionary for storing the values of each state
     
    
   

    

     

    
    

     

       value_table = defaultdict(float)
     
    
   

    

     

    
    

     

       N = defaultdict(int)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 for _ in range(n_episodes):
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # Next, we generate the epsiode and store the states and rewards
     
    
   

    

     

    
    

     

       states, _, rewards = generate_episode(policy, env)
     
    
   

    

     

    
    

     

       returns = 0
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # Then for each step, we store the rewards to a variable R and states to S, and we calculate
     
    
   

    

     

    
    

     
 # returns as a sum of rewards
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 for t in range(len(states) - 1, -1, -1):
     
    
   

    

     

    
    

     

       R = rewards[t]
     
    
   

    

     

    
    

     

       S = states[t]
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

       returns += R
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 # Now to perform first visit MC, we check if the episode is visited for the first time, if yes,
     
    
   

    

     

    
    

     
 # we simply take the average of returns and assign the value of the state as an average of returns
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 if S not in states[:t]:
     
    
   

    

     

    
    

     

       N[S] += 1
     
    
   

    

     

    
    

     

       value_table[S] += (returns - value_table[S]) / N[S]
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 return value_table
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      value = first_visit_mc_prediction(sample_policy, env, n_episodes=500000)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      for i in range(10):
     
    
   

    

     

    
    

     

        print(value.popitem())
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      def plot_blackjack(V, ax1, ax2):
     
    
   

    

     

    
    

     

       player_sum = np.arange(12, 21 + 1)
     
    
   

    

     

    
    

     

       dealer_show = np.arange(1, 10 + 1)
     
    
   

    

     

    
    

     

       usable_ace = np.array([False, True])
     
    
   

    

     

    
    

     

       state_values = np.zeros((len(player_sum), len(dealer_show), len(usable_ace)))
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 for i, player in enumerate(player_sum):
     
    
   

    

     

    
    

     
 for j, dealer in enumerate(dealer_show):
     
    
   

    

     

    
    

     
 for k, ace in enumerate(usable_ace):
     
    
   

    

     

    
    

     

       state_values[i, j, k] = V[player, dealer, ace]
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

       X, Y = np.meshgrid(player_sum, dealer_show)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

       ax1.plot_wireframe(X, Y, state_values[:, :, 0])
     
    
   

    

     

    
    

     

       ax2.plot_wireframe(X, Y, state_values[:, :, 1])
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 for ax in ax1, ax2:
     
    
   

    

     

    
    

     

       ax.set_zlim(-1, 1)
     
    
   

    

     

    
    

     

       ax.set_ylabel('player sum')
     
    
   

    

     

    
    

     

       ax.set_xlabel('dealer showing')
     
    
   

    

     

    
    

     

       ax.set_zlabel('state-value')
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      fig, axes = pyplot.subplots(nrows=2, figsize=(5, 8),
     
    
   

    

     

    
    

     

      subplot_kw={'projection': '3d'})
     
    
   

    

     

    
    

     

      axes[0].set_title('value function without usable ace')
     
    
   

    

     

    
    

     

      axes[1].set_title('value function with usable ace')
     
    
   

    

     

    
    

     

      plot_blackjack(value, axes[0], axes[1])
     
    
  
 

((7, 1, False), -0.6560846560846558)
((4, 7, False), -0.4481132075471699)
((18, 6, False), -0.6899690515201155)
((6, 7, False), -0.5341246290801197)
((17, 8, True), -0.3760445682451254)
((20, 6, False), 0.7093462992976795)
((8, 9, False), -0.5497553017944529)
((4, 4, False), -0.5536480686695283)
((13, 1, False), -0.6560495938435249)
((12, 10, True), -0.20648648648648643)

文章来源: zhangrelay.blog.csdn.net，作者：zhangrelay，版权归原作者所有，如需转载，请联系作者。

原文链接：zhangrelay.blog.csdn.net/article/details/91867331