HDLBits 系列(8)真值表产生工具推荐
目录
原题复现
工具,也只能作为一个参考的工具,我们感谢它的存在,给了我灵感与思路,复习或者纠错等。
例如:
组合表示电路的输出仅是其输入的函数(在数学意义上)。 这意味着对于任何给定的输入值,只有一个可能的输出值。 因此,描述组合函数行为的一种方法是显式列出输入的每个可能值的输出。 这是一个真值表。
对于N个输入的布尔函数,有2N个可能的输入组合。 真值表的每一行列出一个输入组合,因此总会有2N行。 输出列显示每个输入值的输出。
就如下真值表而言:
| Row | Inputs | Outputs | ||
|---|---|---|---|---|
| number | x3 | x2 | x1 | f |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | 1 |
| 4 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 1 |
| 6 | 1 | 1 | 0 | 0 |
| 7 | 1 | 1 | 1 | 1 |
审题
最笨的方法来用电路表达出来,也是:
假设我们要构建上述电路,但仅限于使用一组标准逻辑门。 您将如何构建任意逻辑函数(表示为真值表)?
创建实现真值表功能的电路的一种简单方法是以乘积和形式表示该功能。 乘积的总和(含义为OR)(含义为AND)意味着在真值表的每一行中使用一个N输入与门(以检测输入何时与每一行匹配),然后是一个或门(OR gate),后者仅选择导致结果为 “ 1”输出。
也就是说,用乘累加的方式,或者说用与或式解决。
何况我们本身有着数字电路的基础,我们可以用卡诺图来化简下,更简洁的设计电路,经过化简,我们的输出表达式为:
f = x1 &x3 | x2&(~x3);
我的设计
代入HDLBits
-
module top_module(
-
input x3,
-
input x2,
-
input x1, // three inputs
-
output f // one output
-
);
-
assign f = x1 &x3 | x2&(~x3);
-
-
endmodule
工具推荐
最后,推荐一个自动产生真值表的网站,十分好用。
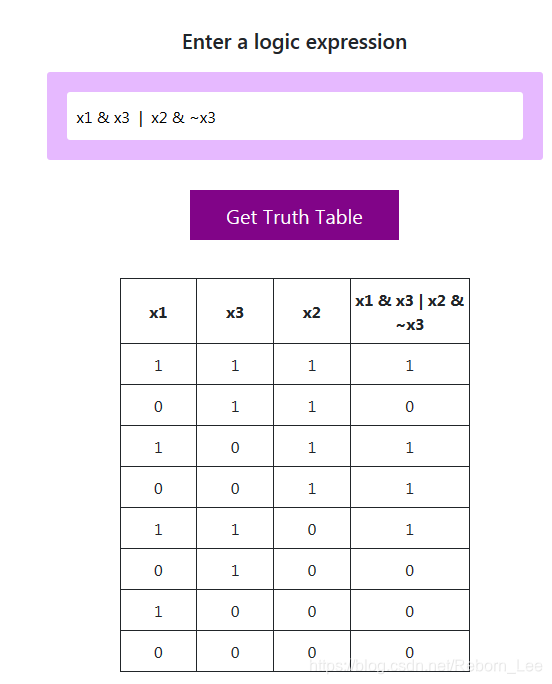
最后,不得不提的是,千万不要把或(|)与加(+)混为一谈丫。
文章来源: reborn.blog.csdn.net,作者:李锐博恩,版权归原作者所有,如需转载,请联系作者。
原文链接:reborn.blog.csdn.net/article/details/103213921
- 点赞
- 收藏
- 关注作者


评论(0)