前言

上篇博客讲的是以时间换空间，前提是时间比较充足，但是为了节省空间，可以做的一些设计。
这里回忆一下，最简单的方法是逻辑合并，可以参看上篇博文，逻辑合并使得组合逻辑更加的复杂，但是减少了触发器的资源消耗，但是组合逻辑的复杂度增加无疑对时间方面不太友好，鱼和熊掌不可兼得，因此属于用时间换空间的策略。
其次，也是最重要的方法是复用，复用大多数针对时序逻辑，可细分为简单提速复用，复杂提速复用以及缓存提速复用，每一种方法针对的情况也各不相同。具体情况，参考上篇博文或者去看看这本书吧。
最后，最重要的是：注！
注：本文摘自《FPGA之道》。

时空变换之空间换时间

本小节我们主要关注当时间不够时，该如何通过以牺牲空间为代价，来换取时间方面余量的提升，即空间换时间的方法。当然，FPGA设计中可以运用空间换时间方法的前提条件是此时空间方面必须具有一定的余量。 那么接下来，就为大家介绍几类比较常用的空间换时间的方法。
注意，时间不够主要体现在以下两方面：
一、规定时间内完成不了任务；
二、规定时钟频率下时序分析通过不了。
其中，第一个方面主要是算法的问题，碰到这种情况首先应该先考虑进行思路转换，看能否想出更加简洁、高效或适合的算法，如果实在不行，才考虑利用空间换时间的方法。而第二方面才是真正的时间余量不足的问题，需要正式采用空间换时间的思路来解决。不过现实中，这两方面在处理的时候经常会发生问题互换，因此经常需要综合考虑。

缓存提速使用

缓存提速使用与【时空变换之时间换空间】章节中介绍的【缓存提速复用】仅一字之差，实际操作中也有很多相似之处，不过其所针对的情况却有本质不同。

• 缓存提速复用，针对处理那些多通道的数据处理，通过模块提速复用，而达到牺牲时间余量来节省资源的目的。
• 而缓存提速使用，针对的是那些单通道的数据处理，由于某些算法在规定时间内完成不了任务，通过模块提速使用，而达到牺牲资源余量（缓存需要消耗资源）和时钟时间余量来缩短任务完成时间的目的。

例如，现在需要对输入数据做如下算法：
假设对于每128个连续的输入数据，若其均值为mean，则找出这128个数中，与mean最接近的那个数X并输出之。那么，为了获得较好的时空特性，可这样设计该算法模块——由于数据是依次输出模块的，因此接收完128个数据后就可以计算出mean。接收数据的时候同时缓存这128个数据，然后接下来再花128个时钟周期将数据依次读出，通过第二遍遍历后得出X。该算法的好处是，求mean的时候只需要使用一个累加器资源（除以128可以用移位或舍去低8位的形式获得），求X时仅需要使用一个减法器和一个比较器资源。不过该算法的缺点是，完成一次求解需要消耗256个时钟周期，可接收数据却只需要128个时钟周期，也就是说该模块每接收128个输入数据后，必须要等待128个时钟周期后，方可再次接收输入数据，因此，若输入数据是连续不断的，该模块的方法将不能胜任。
当然了，也许我们可以想出新的算法，让求解就在128个时钟周期内搞定，不过这样的算法恐怕对资源的消耗过分的大，并且时间方面也会非常紧张，因此，我们还是希望如果能够以此模块为基础，只需略加改动便能适应连续输入的需求，那最好不过。
此时，若该模块本身的时钟余量允许模块被提速运行，并且系统又有额外的缓存资源，那么便可使用缓存提速使用的方法，具体操作如下：
在求解模块输入端口前端建立缓存，将低速输入数据缓存下来，然后提高一倍读取速度进行数据读取并送给求解模块的输入端，同时让求解模块也在提高一倍的时钟速度下工作。这样一来，前端缓存持续输入低速数据，而其输出却是以2倍时钟速度每连续输出128个数据然后等待128个高速时钟周期，那么现在对于求解模块来说，其每接收128个高速输入的数据，正好拥有了256个高速时钟周期的处理时间，而这仅相当于128个低速时钟周期，因此最终缩短了该求解任务的完成时间，达到了以牺牲空间和单周期的时间余量来换取宏观时间余量的目的，满足了系统的需求。
不过由于缓存提速使用牺牲资源作为缓存的同时，也极大的牺牲了时钟周期内的时间余量，因此它也不能算作纯粹的以空间换时间的方法。

模块复制

模块复制与模块复用的思路恰恰相反，因此利用它可以完成以空间换时间的功能。按照其所侧重的方面不同，模块复制的方法又可细分为同频模块复制与缓存降频复制两种，分别介绍如下：

同频模块复制

同频模块复制主要侧重于解决“规定时间内完成不了任务”的问题，它是在不改变模块工作时钟频率的条件下，通过复制出多个模块一起工作，从而到达在缩短任务完成时间的目的。仍以【缓存提速复用】小节中提到的问题为例，倘若求解模块的时钟周期余量不足以支撑其在原时钟2倍速率下的新时钟工作，那么就无法应用缓存提速复用的方法。 不过此时，我们可以通过同频模块复制的方法来解决问题，具体思路如下图：

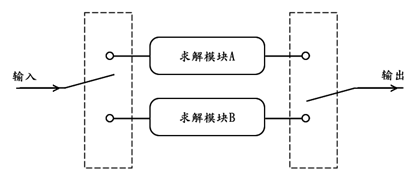
从上图可以看出，同频模块复制，实际上就是采用两个一模一样的求解模块，按照乒乓的方式交替接收输入数据。最开始时，令输入开关接通求解模块A，当求解模块A接收完毕128个连续输入数据后，输入开关接通求解模块B；当求解模块B接收完毕128个连续输入数据后，输入开关又再次接通求解模块A，由于此时求解模块A已经完成了求解，因此可以正常接收新的128个连续输入数据；如此往复便可保证所有输入都得到正确求解。其实从宏观上来看，由于1个模块可以在2T时间内求解完成T时间内接收到的输入，那么2个模块同时工作，就可以在2T时间内求解完成2T时间内接收到的输入，由于求解时间等于接收时间，因此该方案可以用来处理时间上连续的数据流。
参考上例，可知，同频模块复制实际上就是针对解决那些单通道的数据处理问题，通过模块复制的方法，而达到牺牲空间余量来节省任务平均完成时间的目的。

缓存降频复制

缓存降频复制是一种真正意义上的以空间换时间的处理方法，因为它侧重于解决“规定时钟频率下时序分析通过不了”的问题。缓存降频复制是将原有模块的工作时钟频率降低，从而让其获得更多的时间余量，进而通过时序分析，不过由于降频后，该模块的工作效率降低，很可能会导致“规定时间内完成不了任务”的情况，因此降频后，往往还需要引入缓存并继续应用同频模块复制的方法才能保证系统的吞吐量。举例如下：
现在考虑一个略微简单点的问题，即对于每128个连续的输入数据，只需要求解其均值mean，那么据此设计的求解模块，理论上自然可以在每接收完128个连续输入后就给出求解结果，并且可以毫不耽误的开始下一段128个数据的接收和求解。不过如果连续输入数据的速率过快，例如达到200MHz，这很可能会导致该求解模块的时序分析出现问题。对此我们可以采用缓存降频复制的方法来进行解决，思路如下图：

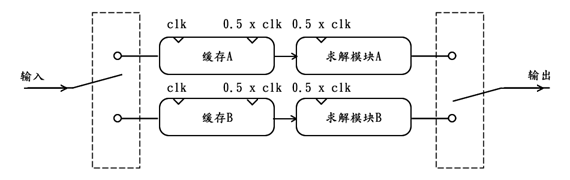
从上图可以看出，为了使得求解模块通过时序分析，不光对其工作时钟进行了降频，还对其进行了复制，并且为了配合降频后的求解模块工作，还需要为每一个求解模块都配备一个缓存来对高频输入数据进行降频处理。如果将添加的缓存与求解模块看做一个整体，上图的工作原理与【同频模块复制】中例子的工作原理几乎一摸一样，因此这里就不再赘述。
参考上例，可知，缓存降频复制也是针对解决那些单通道的数据处理问题，通过先降频，再模块复制，再添加缓存的方法，而达到牺牲空间余量来换取时间余量的目的。

缓存降频使用

缓存降频使用也是一种真正意义上的以空间换时间的处理方法，因为它也侧重于解决“规定时钟频率下时序分析通过不了”的问题。不过与缓存降频复制方法有所不同，缓存降频使用的方法只缓存、降频，却无需复制模块，就可达到以空间换时间的效果。当然了，缓存降频使用具有这样的优点，并不是因为其方法本身比缓存降频复制要优越，而是由于输入数据具有一定的非连续特性，即瞬时数据率虽高，但并不是所有时候都是有效数据。由于这种情况在现实中是比较常见的，因此我们需要掌握缓存降频使用的方法。举例如下：
如果我们对【模块复制->缓存降频复制】小节中的例子稍作改动，即输入数据并不是连续不断的，设源端每连续发送128个数据后就等待128个时钟周期，这样一来，后续的求解模块只需在128 + 128 = 256个200MHz的时钟周期内（1280ns）给出正确结果即可。由于求解模块仅需要128个时钟周期便可得出结果，那么为了充分利用这段时间，可以让其工作在100MHz的时钟频率下，这样求解模块就比较容易通过时序分析，系统的时间余量也会大大增加。不过为了配合低速工作的求解模块，必须在输入与求解模块之间插入缓存，方能降低输入数据的瞬时速度。整个缓存降频使用的方案如下图所示：

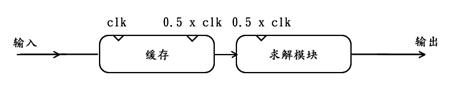
从上图可以看出，缓存降频使用也是针对解决那些单通道的数据处理问题，不过这里主要针对的是非连续型输入，通过添加缓存造成资源膨胀的同时，却对模块达到降频使用的目的，从而很好的实现了以空间换时间的思路。

逻辑拆分

逻辑拆分与【时空变换之时间换空间】章节中介绍的逻辑合并恰恰相反，是用空间换时间时，最常用、也是最简捷有效的一种做法。它的基本思路是将寄存器插入到组合逻辑的路径上，从而将原本延迟较大的组合逻辑拆分成两个延迟较小的组合逻辑，进而在增加了寄存器资源的情况下，缩小了组合逻辑的时间延迟，通过改善“最短板”，达到提升系统时间性能的目的。当然了，前提仍是这样做不会改变原有电路的功能。
关于逻辑拆分的具体做法和例子，大家完全可以参考【时空变换之时间换空间->逻辑合并】小节，只不过参考的时候，需要颠倒过来分析和理解即可。
通常来说，如果逻辑电路的工作时钟频率较高，那么对系统的时间要求也较高，此时通常需要做逻辑拆分；如果逻辑电路的工作时钟频率较低，那么对系统的时间要求也较低，那么通常需要做逻辑合并。

流水线

流水线是逻辑拆分思想的升华，是一种高级的以空间换时间的思路，在FPGA的设计中应用十分广泛，下面就对流水线的设计思路进行详细介绍。

流水线的由来

在FPGA设计中，应用的流水线思路，其实是受到了工厂里面“流水式生产线”工作模式的启发。
在工厂里，“流水式生产线”是一种非常好的提高生产效率的工作方式，当然，相比“单兵作战”，它需要投入更多的人工，下面就让我们来看一下“流水式生产线”的产生过程。
比方说，你有一个将纸板加工成纸箱子的工厂。一个工人独立生产一个纸箱子需要30分钟时间，而他需要做的工作可粗略分为以下三个环节：裁剪纸张、粘贴成箱、箱体上色，每个环节耗时均为10分钟，分别需要使用到的主要工具为剪刀、胶水、彩笔。
那么，如果由一个工人独立生产箱子的话，按一天工作8小时计算，共可生产16个。假设你工厂一天的订单量为48个，那么如果采用这种“单兵作战”的模式肯定是来不及，因此你共需要雇佣3个工人，并且要购买3把剪刀、3管胶水、3个彩笔，这样才能完成订单要求的工作量，不过由于每个工人的工作模式仍是“单兵作战”，因此这种生产模式也称之为“无协作式生产”。
俗话说，“熟能生巧”，既然生产纸箱子共分为三个工作量一样的环节，并且你又雇佣了3个工人，那如果让每个工人专注于不同的环节，效果会怎么样呢？这样做的好处显而易见。首先，如果每个工人只关注一个环节，那么你值需要购买1把剪刀、1管胶水、1个彩笔，节省了很多工具。其次，由于每个工人仅专注于一个生产环节，那么时间长必定“熟能生巧”，这样也许可以将每个环节的耗时再减少几分钟，从而每天可以生产出来更多的箱子。这便是“流水式生产线”的工作方式。
综上所述，我们可以总结出“流水式生产线”为生产带来的好处，那就是它极大的提高了工作效率，虽然每一个箱子仍然需要经过3道工序才能完工，总耗时30分钟（工人保持原有的工作效率），但是由于同时有3个工人负责不同的工序，因此给人的感觉是每10分钟就可以生产出一个成品箱子，并且各种工具的利用率也提高到了100%。
当然了，“流水式生产线”也存在一定的制约。

• 首先，后一个环节的有效工作必须建立在前一个环节的有效工作基础上。例如，如果负责裁剪的工人今天请假，那么这一天一个纸箱子也别想生产出来。
• 其次，从输入到产出有一定的延迟，因此输入、输出没有直接对应关系。例如，“流水式生产线”这一刻输出的纸箱子，并不是这一刻输入的硬纸板制作的，而是30分钟前送入的硬纸板制作的。
• 第三，如果流程环节分得太细，将会消耗过多的人力，得不偿失。

对应到FPGA的设计中，将一段较为复杂的逻辑功能分成若干个环节来实现，只要保证所有环节都能同时工作，就可以极大的提高FPGA系统的时间效率，不过其代价就是要增加一些中间缓存单元，这便是以空间换时间的流水线思路。
而流水线思路的制约也有三点：

• 首先，若流水线为N级（即将原逻辑功能分为N个环节），每级平均耗时为T，那么前NxT时间内，最后一个级的输出没有任何意义。
• 其次，流水线的输入与输出之间的对应存在延迟关系，而这个延迟可能会对逻辑电路带来隐患。
• 第三，如果流水线添加的不恰当，有可能会造成资源的极度膨胀。

因此，流水线虽好，但是鉴于这三点制约，我们在使用它解决问题的时候还是应该考虑周全，下面就给出几种主要的流水线使用方法。

如何在组合逻辑中使用流水线

针对组合逻辑使用流水线，主要是解决“规定时钟频率下时序分析通过不了”的问题，这也是比较常见的流水线应用场合。它的原理同【逻辑拆分】小节中的介绍，只不过流水线的思路往往将一个组合逻辑拆分成更多段而已。
例如，输入X先加5，再取反，再减7，结果才为输出Y，若不采用流水线，原理结构图如下：

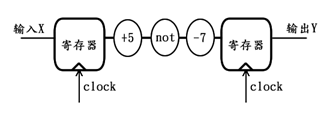
若采用3级流水线的思路，其修改后的原理结构图如下：

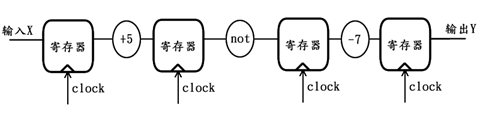
对比以上两图可见，对原组合逻辑采用了流水线思路之后，虽然多消耗了2组寄存器资源（跟数据位宽相关），但整个逻辑电路的时间性能得到了极大的提升，可以工作在更加高速的时钟频率下，因此极大提高了整个逻辑的最高数据吞吐量。

如何在时序逻辑中使用流水线

针对时序逻辑使用流水线，主要是解决“规定时间内完成不了任务”的问题，其思路是按照功能对算法进行拆分。仍以【缓存提速复用】小节中提到的问题为例，由于求解mean需要128个时钟周期，求解X又需要128个时钟周期，只要我们利用流水线的思路，将求解mean和求解X这两个工作设计为可同时工作的两个独立环节，便可以使得整个求解模块每128个时钟周期就完成一次求解，因此便可以满足系统对连续输入的处理需求。
下图给出对该时序逻辑应用流水线思路后的原理图：

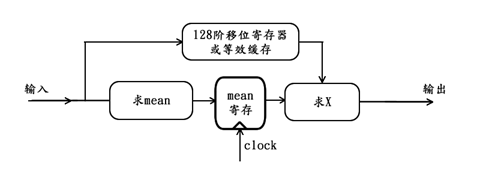
上图中，由于mean寄存的引入，再加上128阶的输入数据缓存，将求mean算法和求X算法分割成独立的两部分。当这两部分同时工作时，求mean算法完成对当前连续输入的128个数的求解时，求X算法刚刚完成对上一次连续输入的128个数的求解，因此系统对应的输入与输出之间具有128个周期的延迟（即一个求mean或求X算法的耗时）。由此可见，该时序逻辑应用了流水线的思路后，仅增加了一个mean寄存，但却极大的缩短了平均任务完成时间。

顺序系统中如何正确添加流水线

添加流水线并不仅仅是将一块逻辑用缓存单元分成很多个小块逻辑而已，从系统的层面来讲，这种流水线的划分势必会对整个系统的行为造成影响，这是因为该块逻辑添加流水线前后，输入与输出之间的延迟时钟周期数明显不同，那么，为了确保系统仍能给出正确的输出，必须对系统的其他部分进行相应的调整。那么，本小节就主要针对顺序系统，来介绍正确添加流水线的思路。
顺序系统指的是其内部数据流从系统输入端出发，逐级传递，最后经由系统输出端流出的系统。例如下图所示逻辑电路即为一个顺序系统：

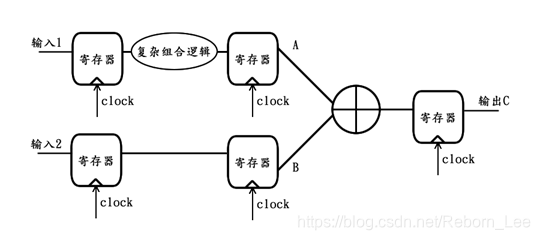
上图电路的功能大致为，输入1经过特定处理后，与输入2相加，到输出C。由于输入1的特定处理为复杂组合逻辑，为了提高该系统的时间性能，现打算对其应用流水线思路，若添加的流水线为3级，则上图变形为：

仔细观察就会发现，上图和原先的系统行为并不等价。对于求出C的加法来说，如果之前系统的算式为：
C0 = A0 + B0；
C1 = A1 + B1；
……
那么，我们希望添加了流水线后的系统，其输出也应该满足：
Cx = An + Bn；（其中，x和n的差别即为流水线所引入的延迟）
可是由于流水线仅仅针对输入1，这将导致上图的输出公式实际等于：
Cx = A_(n-2) + Bn；
为了纠正这点，必须在输入2的分支也添加2级寄存器，来达到A、B延迟的平衡。修改后的逻辑图如下：

综上所述，对于顺序系统来说，如果要对其并行分支中的一个分支应用流水线，为了保证系统整体行为的正确性，还必须对其他并行分支也一并应用，即便在其他并行分支的时间性能已经非常好的情况下。一个比较常见的例子就是当我们处理非连续数据时，由于每个有效数据都会配合一个有效的使能标志，因此，如果在数据处理阶段应用了流水线，则必须对使能标志应用同周期数的延迟，这样输出数据和输出使能才能正确配对。

反馈系统中如何正确添加流水线

如果系统中的数据流并不完全是逐级传递的，而是存在反馈回路，那么这样的系统即为反馈系统。对于反馈系统来说，要想正确的添加流水线就没那么容易了，因为流水线会增加时钟周期延迟，而周期延迟必定改变反馈回路的作用。本小节就以一个具有反馈的乘法器作为例子，来详细分析反馈系统中流水线的正确添加方法。
若该反馈乘法器系统的原理图如下：

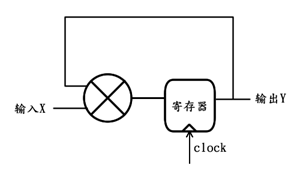
则其对应的公式为：
Y[n+1] = Y[n] * X[n];
若输入序列X[n]为：
1、2、3、4、5、……，
寄存器初始值为1，则输出序列Y[n]为：
1、1、2、6、24、120、……
由于乘法运算的延时比较大，那么为了提高该反馈系统的时间性能，我们希望对乘法运算应用流水线。可是此时不能简单的应用逻辑拆分的原理，因为若仅仅简单的对乘法应用2级流水线，则原理图变为：

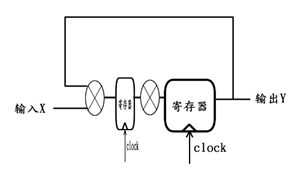
上图等效如下：

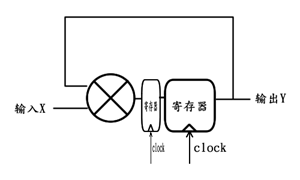
则其对应公式为：
Y[n+2] = Y[n] * X[n];
此时，对于同样的输入序列X[n]，若寄存器初始值均为1，则输出序列Y[n]为：
1、1、1、2、3、8、15、48、……
由此可见，修改后的反馈系统与原反馈系统的输出完全没有对应关系，因此反馈系统的流水线不能通过简单的逻辑拆分得出。
添加流水线的思路无非是想在组合逻辑中多增加几级寄存器而已，那么我们不妨对原反馈系统的公式进行简单变换，让其反馈间隔增大看看。
由于，
Y[n+1] = Y[n] * X[n];
那么，
Y[n] = Y[n-1] * X[n-1];
因此，
Y[n+1] = Y[n-1] * X[n-1] * X[n];
这样一来，新的公式中，Y[n+1]使用到的反馈就不是来自仅一级寄存器之隔的Y[n]，而是来自两级寄存之隔的Y[n-1]。上述公式对应的原理图如下：

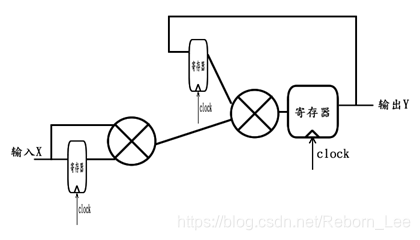
可以令
B[n] = X[n-1] * X[n];
对于这个子系统，由于没有反馈存在，所以可以应用流水线提升时间余量，所以最终公式为：
B[n+p+1] = X[n-1] * X[n];
其中p为流水线的级数，加1是为了保证最后一级组合逻辑也被寄存输出。
因此，只要保证B[0]~B[p+1]均为1，所有寄存器初值均为1，则
Y[n+1] = Y[n-1] * B[n+p+1];
与
Y[n+1] = Y[n-1] * B[n];
之间，除了输出序列相比会晚p+1个周期外，不会再有别的变化。因此上图可化简为：

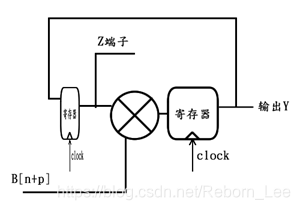
注意上图中的Z端子，它其实也只比输出Y晚了一个时钟周期罢了，因此若以Z端子作为输出，仍能保证该反馈系统输出的正确性，所以逻辑电路图可变形如下：

类似的 ，对于这个乘法可使用2级流水线的思路，不过此时无须插入寄存器，只需做retiming即可。
下面来验证上述变换的正确性：
仍然对于同样的X[n]输入序列，假设产生B的流水线级数p = 2，那么B[n+p+1]如下：
1、1、1、2、6、12、20、……
若上图中的所有寄存器初值均为1，则Z[n]如下：
1、1、1、1、1、2、6、24、120、……
对比Y[n]应有的取值，可知Z[n]仅仅比其滞后3个时钟周期。最终的流水线方案如下图：

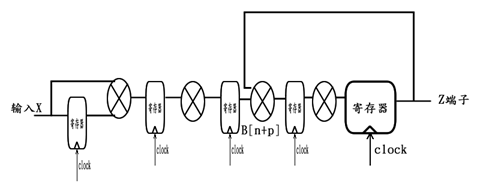
注意，上图中并没有给出具体的逻辑拆分方法，只是形象的将每一个乘法都划分为两级流水来进行作业，因此整个系统具有较好的时间特性。

通过上述分析，我们可以总结出反馈系统中添加流水线的一般方法如下：
首先，反馈系统的输入、输出之间的关系通式如下：
y[n+1] = fa1(y[n], y[n-1], y[n-2], ……) + fb1(x[n], x[n-1], x[n-2], ……); ——(1)
如果要在反馈系统中添加K级流水线，可先通过公式推导，得出y[n+1]与y[n-K+1]、y[n-K]、……之间的反馈关系式。方法很简单，令n = n-1，那么(1)式变为：
y[n] = fa1(y[n-1], y[n-2], y[n-3], ……) + fb1(x[n-1], x[n-2], x[n-3], ……); ——(2)
因此，将(2)式代入(1)式中，即可得到y[n+1]与y[n-1]、y[n-2]、……之间的反馈关系式如下：
y[n+1] = fa2(y[n-1], y[n-2], y[n-3], ……) + fb2(x[n], x[n-1], x[n-2], ……); ——(3)
若令n = n-2，(1)式又可变为
y[n-1] = fa1(y[n-2], y[n-3], y[n-4], ……) + fb1(x[n-2], x[n-3], x[n-4], ……); ——(4)
将(4)式代入(3)式，则可得到y[n+1]与y[n-2]、y[n-3]、……之间的反馈关系式，如此反复，则可最终得到y[n+1]与y[n-K+1]、y[n-K]、……之间的反馈关系式如下：
y[n+1] = faK(y[n-K+1], y[n-K], y[n-K-1], ……) + fbK(x[n], x[n-1], x[n-2], ……); ——(5)
现在，求解y[n+1]分为两大部分——函数faK部分与函数fbK部分。
由于fbK()中全部是跟输入序列x[n]相关，并且没有反馈存在，因此无论其逻辑多么复杂，都可以采用顺序系统中添加流水线的方法来提高其工作时钟频率，只不过会造成fbK()函数的输出序列产生相应流水级数加1的延迟（加1是因为希望最后与faK()函数进行运算的结果为寄存输出，而不是组合输出）。
当然了，为了保证fbK()的输出延迟也仅造成y[n+1]序列的整体延迟，必须保证faK()的输出值也能具有同数量级的延迟，而这点可以通过对寄存器赋初值（有时候不适用），或对faK()算子添加计数使能标志，使其只有在fbK()给出有效数据后才开始工作即可。
鉴于此，可以将fbK()函数用序列fbK[n]代替，则(5)式简化为：
y[n+1] = faK(y[n-K+1], y[n-K], y[n-K-1], ……) + fbK[n]; ——(6)
该公式对应的电路原理图如下：

由于y[n-K+1]相比于y[n]序列也仅仅是滞后K-1个时钟周期而已，那么若令y[n-K+1]作为系统的输出端，则上图又可变形为：

由此可见，组合逻辑faK(……) + fbK[n]之后，输出y[n-K+1]的寄存器之前，共有K-1个寄存器组成移位寄存器阵列。由于这些寄存器之间仅有线延迟而已，因此局部时间性能优越，正好可以利用这组移位寄存器阵列，来对组合逻辑faK(……) + fbK[n]做retiming（即分布调整），从而完成整个反馈系统的K级流水线设计。最终设计结果原理图如下：

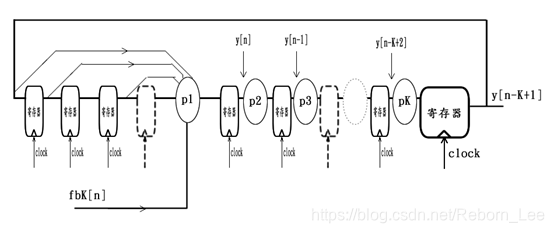
综上可见，反馈系统正是通过公式迭代的方法，来在原先逻辑电路的结构中产生出一组纯净的移位寄存器阵列，并利用此来做流水线，从而达到以空间换时间的目的。

使能链

之前介绍的缓存提速使用的方法，主要侧重于解决“规定时间内完成不了任务”的问题的，它是以牺牲空间和单周期的时间余量来换取宏观时间余量的一种方法。而本小节要介绍的使能链方法与之有些类似，也算不上是纯粹的以空间换时间的方法，不过与缓存提速使用有所不同，使能链主要侧重于解决“规定时钟频率下时序分析通过不了”的问题，并且它是以牺牲空间和宏观时间余量来换取单周期时间余量的一种方法。
使能链从形式上来看，与流水线非常类似，都是将一个复杂的逻辑划分成很多个部分来处理，不过不同的是，流水线的思路是要让每一个部分都同时工作，而使能链的思路却是要让每一个部分依次进行工作。因此，两种思路的共同特点都是会提升系统单时钟周期的时间余量，但相比之下，流水线能够提升系统的工作效率和吞吐量，而使能链则往往会降低系统的工作效率和吞吐量，不过由于每次仅有一个模块在工作，因此其功耗一般较低。对比【本篇->编程思路->状态机，FPGA的灵魂->状态机的设计->状态机群的设计】小节中的介绍，可知，流水线的工作模式就类似于串联式状态机群，而使能链的工作模式就类似于串行式状态机群。
那么，为了能够让逻辑拆分后的各个部分依次工作，就需要用到使能链。使能链，其实就是一个环形移位寄存器阵列，该阵列中的寄存器，在初始时，仅有一个为逻辑1，其余均为逻辑0（反之亦可，取决于有效电平），这样一来，该逻辑1便会随着时钟信号的脉搏，在使能链中逐步移动，若以此使能链作为各部分逻辑是否工作的使能，则可以很好的控制各部分逻辑依次有序的进行工作。
例如，对于【流水线->如何在组合逻辑中使用流水线】小节中的例子，将其修改为使能链的结构，原理图类似如下所示：

通过上图，我们可以了解使能链的工作模式：
系统初始时，使能链中，仅有对应“输入X”的寄存器输出为逻辑1，因此系统最开始工作时，采集输入X的逻辑部分最先开始工作，获取第一个输入采样x0。
第1个时钟周期过后，使能链中仅有对应“+5”的寄存器输出为逻辑1，因此在第2个时钟周期内，“+5”的逻辑电路在“输入X”电路的基础上开始工作，计算出x0+5的值。
第2个时钟周期过后，使能链中仅有对应“not”的寄存器输出为逻辑1，因此在第3个时钟周期内，“not”的逻辑电路在“+5”电路的基础上开始工作，计算出(x0+5) ̅的值。
第3个时钟周期过后，使能链中仅有对应“-7”的寄存器输出为逻辑1，因此在第4个时钟周期内，“-7”的逻辑电路在“not”电路的基础上开始工作，计算出(x0+5) ̅ - 7的值。
第4个时钟周期过后，使能链中仅有对应“输出Y”的寄存器输出为逻辑1，因此在第5个时钟周期内，“输出Y”的逻辑电路在“-7”电路的基础上开始工作，将(x0+5) ̅ - 7的最终结果输出至Y端。
第5个时钟周期过后，使能链中又仅有对应“输入X”的寄存器输出为逻辑1，因此在第6个时钟周期内，采集输入X的逻辑部分开始第二次工作，获取第二个输入采样x1……如此往复。
对于那些当前时刻，对应使能链中寄存器的输出为逻辑0的那些逻辑部分，由于没有获得有效的使能信号，它们将处于休眠状态，其输出不会有任何变化。
综上所述，使能链的方法以牺牲资源（使能链本身、拆分逻辑所用的寄存器等）、牺牲系统宏观时间余量（完成一件事消耗更多的时钟周期）来换取单周期时间余量（每一部分逻辑的延迟比以前小了）的一种方法。因此，使能链通常更适用于“主动采集”形式（即输入数据是在电路想要的时候才进行采集的，不需要的时候不去采集）的低吞吐逻辑电路，而对于“被动采集”形式（即输入数据有其自身的频率，并且必须以这个频率被接收）的高吞吐逻辑电路，则最好采用流水线的形式来完成。

文章来源: reborn.blog.csdn.net，作者：李锐博恩，版权归原作者所有，如需转载，请联系作者。

原文链接：reborn.blog.csdn.net/article/details/104654855