FPGA之道(76)静态时序分析(二)一道时序分析的例题
前言
本文来自于《FPGA 之道》,在正式讲解时序分析之前,作者给出了一道时序分析的例题,体会下人工分析时序的例子,挺有意思,一起看下。
时序分析在FPGA当中,算是有点烧脑的内容,通过都是通过画图的方式理解,比较通俗,毕竟描述起来比较抽象,但是今天这篇博文不通过这种方式,仅仅通过语言描述来解释 ,一起看看。
一道时序分析的例题
让我们先抛开相关的时序分析工具,通过一个非常简单的例子,来了解一下,如何通过人脑来进行时序分析。
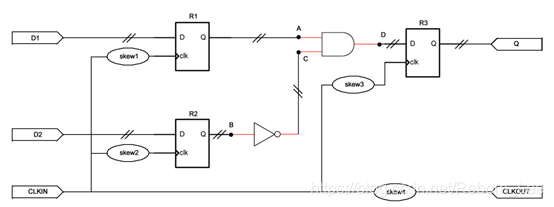
假设FPGA中实现的数字电路如下图所示,已知:
- 1、寄存器R1、R2、R3的参数一致,其建立时间要求均为2ns,保持时间要求均为1ns,tco均为1.5ns;
- 2、时钟信号从输入管脚到达到达各个寄存器的时间具有一定差别,其中skew1、skew2、skew3、skew4分别为4ns、3ns、5ns、6ns;
- 3、所有数据线的线延迟tLine均为2ns(图中“//”所示);
- 4、非门的门延迟为2ns,与门的门延迟为3ns;
- 5、输入时钟CLKIN为50MHz理想时钟,输入数据D1、D2的采样率也为50MHz,它们的slew rate均为理想情况(无穷大),并且时钟的有效边沿上升沿对齐数据的中心;
- 6、输出端要求数据Q相对于CLKOUT的上升沿至少具有3ns的建立时间和2ns的保持时间。
问题:
- 1、FPGA芯片是否能够正常工作?
- 2、如果能够正常工作,CLKIN所支持的最大频率(D1、D2所支持的最大采样率)是多少?
- 3、若skew3为15ns,情况会有什么变化?
解答一:能否正确工作分析
上述FPGA芯片能否正常工作取决于两个条件:第一,其内部的各个寄存器能否正常工作;第二,Q与CLKOUT的关系能否满足后级电路的要求。如果再细分的话,FPGA芯片能否正常工作取决于三个条件:第一,能否正确的采集外部数据;第二,FPGA内部能否正确的处理数据;第三,FPGA的输出是否满足后级电路的要求。
而对于三个条件的划分方法,条件一和条件三尽管数据流方向不同,但其共性都是跟外界打交道,因此可以综合称之为FPGA的接口条件。相对应的,条件二可称之为内部时钟条件。
首先,为整个FPGA设计指定参考0时刻,并令0时刻时,CLKIN处正好迎来一个时钟的上升沿。
由于本例电路中的寄存器,在每个时钟有效边沿时刻所面临的工作状态都是一样的,因此,对于每一个寄存器以及后级电路,我们只需要分析1个边沿情况即可。
那么,以0时刻的时钟上升沿为参考,对于寄存器R1来说,有效时钟上升沿传递到其时钟端口的时间是0ns+skew1 = 4ns, 显然,正常工作时,它是应该正确采样到D1端口从-10ns持续到10ns的数据符号。由于2ns线延迟的影响,导致R1的D端口上对应的数据稳定区间应该是-8ns~12ns。 据此可以求出寄存器R1的建立时间和保持时间如下:
tsu = 4 - (-8) = 12 ns;(由于建立时间的定义是时钟上升沿到来之前数据保持稳定的时间,
时钟到达会有4ns的延迟,因此有利于建立时间满足,这里的4ns会放进建立时间里面,因此
这样建立时间相当于4 + 8 = 12,上面用减法仅仅是因为假设了0时刻,0时刻之前的8ns
在符号上标记为负号。这段解释不用看了,省的费脑子!)
th = 12 - 4 = 8 ns;
- 1
- 2
- 3
- 4
- 5
由于tsu ≥ 2ns、th ≥ 1ns,故R1可以正常工作。
同理,可得R2的建立时间和保持时间如下:
tsu = 3 - (-8) = 11 ns;
th = 12 - 3 = 9 ns;
- 1
- 2
可见R2也可以正常工作。
而对于寄存器R3来说,由于它是R1、R2的后级,因此传递到它的时钟上升沿应该正确采集到上一个时钟上升沿所导致R1、R2的输出变化所驱动的逻辑电路结果。(此时,我们可以不去管R1、R2事实上能否正常工作,只需要假设其已经正常工作即可,因为这里我们的目的是关注于R3的输入驱动逻辑电路部分。)那么,若我们以CLKIN处20ns的时钟上升沿为R3的判断参考,则其应该正确采集到CLKIN处0ns时钟上升沿所驱动的R1、R2的输出逻辑结果。
我们先来看一下R3的clk端口,对应于20ns时CLKIN处的时钟上升沿,其传递到R3的clk端口时间为20ns+skew3 = 25ns。
而对于R3的D端口来说。仔细观察R3的输入驱动逻辑电路,可以发现其存在两条路径,第一条为从R1的Q端出发,经由与门后到达R3的D端;第二条为从R2的Q端出发,经由非门后再经由与门到达R3的D端。
以0ns作为参考时刻,分别计算两条路径的延迟如下:
T_road1 = tRef + skew1 + tco + tLine + tAnd + tLine =
0 + 4 + 1.5 + 2 + 3 + 2 = 12.5 ns;
T_road2 = tRef + skew2 + tco + tLine + tNot + tLine + tAnd + tLine =
0 + 3 + 1.5 + 2 +2 + 2+ 3 + 2 = 15.5 ns;
- 1
- 2
- 3
- 4
而以20ns作为参考时刻,分别计算两条路径的延迟如下:
T_road1 = 32.5 ns;
T_road2 = 35.5 ns;
- 1
- 2
那么,对于R3来说,由于其前端组合逻辑电路结果的稳定开始时间取决于其前级寄存器被上一边沿事件驱动后的最大延迟路径;而其稳定结束时间则取决于其前级寄存器被当前边沿事件驱动后的最小延迟路径。因此其D端口的数据显然是从15.5ns才开始稳定,并持续到32.5ns结束,稳定周期17ns,通常都会小于时钟周期20ns。
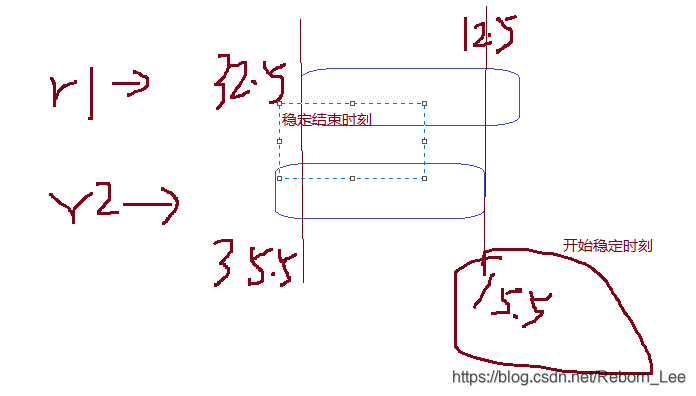
据此可以求出寄存器R3的建立时间和保持时间如下:
tsu = 25 - 15.5 = 9.5 ns;
th = 32.5 - 25 = 7.5 ns;
- 1
- 2
可见R3也能正常工作。
最后,我们来分析Q与CLKOUT之间的关系是否满足要求。为了便于理解,我们可以假想在FPGA的外部有一个寄存器R4,其建立时间要求和保持时间要求分别为3ns、2ns,而Q和CLKOUT分别连接至R4的D端和clk端,这样问题便转化为R4是否能够正常工作了。同理,我们仍无需关心R3是否能够正常工作,以20ns时,CLKIN处的时钟上升沿做为R4的参考,可得其传递到R4的clk端的时间为20ns+skew4 = 26ns。而从R3的输出端到整个FPGA的Q端只有一条纯线延迟路径,所以,以0ns作为参考时刻,计算路径的延迟如下:
T_road = tRef + skew3 + tco + tLine = 0 + 5 + 1.5 + 2 = 8.5 ns;
而以20ns作为参考时刻,计算路径的延迟如下:
T_road = 28.5 ns;
- 1
- 2
- 3
因此其D端口的数据显然是从8.5ns开始稳定,并持续到28.5ns结束,由于只有一条路径,所以稳定周期与时钟周期一样,均为20ns。
据此可以求出寄存器R4的建立时间和保持时间如下:
tsu = 26 - 8.5 = 17.5 ns;
th = 28.5 - 26 = 2.5 ns;
- 1
- 2
可见R4也能正常工作。
- 1
结论,FPGA芯片在上述电路及输入、输出条件下,可以正常工作。
解答二:最大时钟速率分析
还记得上一小节中虚拟出来的寄存器R4么?所谓FPGA正常工作时CLKIN所支持的最大频率,其实就是要确保R1、R2、R3、R4均正常工作时,CLKIN所允许的最高频率。
对于R1来说,设时钟周期为T(显然T≥0),则根据其建立时间、保持时间及建立时间要求和保持时间要求,可得如下一组不等式:
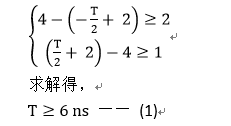
类似的,对于R2可得如下一组不等式:

而对于R3,我们以参考时钟边沿的上一边沿最长路径和当前边沿最短路径,可得其正常工作时,建立时间和保持时间的不等式组如下:
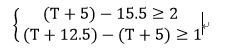
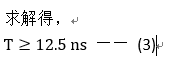
仔细观察R3不等式组中的第二个等式,这是确保保持时间满足要求的不等式,其化简后为
7.5≥1
是个完全确定的不等式,这其实反映了针对内部时钟条件所涉及寄存器的两个事实:一、保持时间是否满足,跟时钟周期和频率没有关系;二、如果保持时间不满足,想通过调整时钟速度来解决是不可行的。
对于虚拟的R4,也可类似得出不等式组如下:
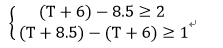
求解得,
T≥4 .5ns —— (4)
虽然R4不等式组中的保持时间确保不等式化简后也是一个确定的等式,但请注意,输出接口并不一定都是可以用虚拟寄存器来处理的。
综合(1)、(2)、(3)、(4)式,可得,令R1、R2、R3、R4均正常工作的T必须满足
T≥12.5 ns
因此,CLKIN所支持的最大时钟频率为80MHz。
通常,基于系统的稳定性、可靠性等方面的考虑,我们需要让FPGA设计的时钟工作频率具有一定余量,例如,通常的指标是10%或20%。如果以20%为例,那么本例的时钟余量为
(80-50)÷80×100%=37.5%
可见,满足时钟余量要求。
延伸二:最小时钟速率?
经过上一章节的介绍,也许你会忍不住问,为什么我们往往碰见的都是求时钟最大频率的情况?简单解释一下:首先,频率越高的逻辑越难实现,频率越低的逻辑越容易实现,这是毋庸置疑的。而且时钟频率越高,意味着性能也就越好,而性能的提高总是面临各种各样阻碍的,因此其每次提升必然是有限度的。这就好比对于汽车,厂家都会拿其最大时速出来说事。其次,从本章节中关于寄存器的保持时间不等式可以看出,除了和外界直接打交道的寄存器,其余寄存器的保持时间跟时钟频率本身没有关系,但它们的建立时间则往往受限于时钟频率。为了能够满足寄存器的建立时间要求,时钟周期不能太小,否则在下一个上升沿到来之前,驱动其D端的组合逻辑可能还没有稳定,因此任何时序逻辑的时钟频率都会有一个上限。第三,物理硬件、环境因素的一些限制,也决定了FPGA内部时钟信号的频率一定存在上限。
那么,有没有求时钟最小频率的情况呢?老实说,也是有的,但这往往并不是时序分析所需要涉及的工作。例如由于硬件资源的限制,像PLL、DCM这种本身对输入时钟频率范围的限制,导致太低频的时钟并不能完成锁定;又例如由于功能的限制,类似异步串口这样的数据接收,对于一个异步数据的符号位至少要进行3倍以上的重采样,如果所选的采样时钟频率太低,则不能实现异步通信功能;等等。
不过,对于一些非常规的时序问题,可能真是需要求时钟频率下限的。例如,以本章节最开始的例子为基础,若线延迟变为10ns,并且我们期望0时刻的CLKIN上升沿在R1处采集的是-T时刻CLKIN上升沿对应的D1上的数据,那么,如果我们仅仅关注R1寄存器部分逻辑电路的话,此时关于其的建立和保持不等式变为:
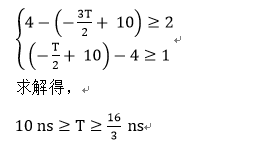
可见,此时时钟信号的频率除了具有上限187.5MHz之外,还具有下限100MHz。
解答三:保持时间不足情形分析
若skew3变为15ns,则根据【解答一:能否正确工作分析】小节中关于R3的分析,可知,对应于20ns时CLKIN处的时钟上升沿,其传递到R3的clk端口时间为20ns+skew3 = 35ns。可是其D端口的对应数据是从15.5ns开始稳定,并持续到32.5ns结束。据此可以求出寄存器R3的建立时间和保持时间如下:
tsu = 35 - 15.5 = 19.5 ns;
th = 32.5 - 35 = -2.5 ns;
由于保持时间为负数,显然R3的保持时间要求得不到满足,这便是保持时间不足的情况。根据【解答二:最大时钟速率分析】小节中关于保持时间不等式的分析,可知,保持时间仅与电路中的各类延迟参数有关,而与时钟的速率无关,因此碰到这种问题往往是时钟信号skew差异过大所导致的。此时,即便tsu看似满足R3的建立时间要求,其充其量也只能算是一种“伪满足”,因为对于一个稳定时间长度不能持续到R3时钟有效边沿到来前2ns(对于35ns的R3时钟边沿来说,这个值是33ns)的数据信号来说,其根本就不能对R3的输出结果产生影响;即便其可以持续到2ns以内,但由于保持时间得不到满足,R3的输出便呈现出亚稳态,从而其输出在后级看来便是不对的或不确定的。
文章来源: reborn.blog.csdn.net,作者:李锐博恩,版权归原作者所有,如需转载,请联系作者。
原文链接:reborn.blog.csdn.net/article/details/105098351
- 点赞
- 收藏
- 关注作者


评论(0)