前言

本文来自于《FPGA 之道》。

同步时序逻辑的分析原理

FPGA设计中最最常见并且占FPGA设计比重最大的就要数同步时序逻辑了，那么，经过了上一章节中示例的分析，接下来就让我们来简单了解一下针对同步时序逻辑的时序分析原理。

逻辑锥的概念

以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的面所围成的旋转体就叫做圆锥，如下图所示：

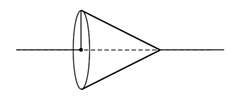
而在同步时序逻辑中，对于一个与外界没有直接联系的内部寄存器，其输入端D上的数据信号肯定是由其它一些寄存器的输出端Q经由一个组合逻辑网络所驱动的。那么，如果把该寄存器看做圆锥的顶点，驱动其D端口数据信号的那些寄存器看成圆锥的底面，而中间的组合逻辑网络看成椎体的话，便可以在FPGA设计所对应的数字逻辑电路中得到一个类似圆锥的子结构，我们称其为——逻辑锥。

逻辑锥的划分

对于纯同步时序逻辑来说，不仅仅是那些决定内部时钟条件的寄存器，甚至连那些直接和芯片外部交互的寄存器，也都可以有属于自己的逻辑锥。以【本篇->时序分析的原理->一道时序分析的例题】章节中的例题为例，我们不光可以在其输出端口虚拟一个R4，同样也可以在其输入端口虚拟出R5与R6，只不过需要根据时钟、信号间的具体时间延迟情况来赋予R5、R6不同的tco等时间参数罢了。那么，针对该例进行逻辑锥划分的结果如下图所示：

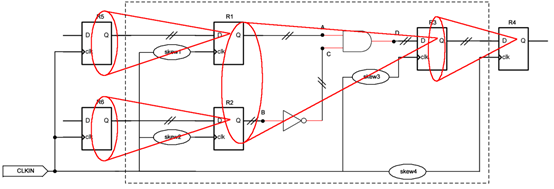
可见，4个逻辑锥的顶点分别为R1、R2、R3、R4，它覆盖了整个FPGA电路能否正常工作所关心的条件。
只要一个逻辑锥底面上的那些寄存器能够正常工作，那么对于该逻辑锥来说，其内部各个信号的时间延迟参数就不会跟前级的逻辑锥有任何关系。这也是寄存器为什么可以打断时延路径的原因，从而让任何门延迟和线延迟都无法穿透寄存器而继续传递下去。因此，以前级逻辑锥可以正常工作为前提，一个逻辑锥顶点所对应的寄存器能否正常工作完全取决于其内部所包含的寄存器和组合逻辑的相关时间参数及延迟特性。
按照上述假设条件去分析FPGA设计中的每一个逻辑锥，如果每个逻辑锥都能正常工作的话，那么整个FPGA设计能否正常工作就仅依赖于第一级逻辑锥底面的寄存器能否正常工作了。由于第一级逻辑锥底面的寄存器都是虚拟出来的（例如上图中R5、R6），所以我们早已在虚拟的时候假设其能够正常工作了。因此，若每个逻辑锥都能正常工作的话，则整个FPGA设计就能正常工作；反之，若某一个逻辑锥不能正常工作，则整个FPGA设计就存在时序问题，并且由于错误是可以传递的，整个FPGA的行为就可能“差之毫厘，谬以千里！”
事实上，无论多么复杂、多么庞大的同步时序逻辑，都可以很容易的将其划分为逻辑锥的集群（当然，这要依赖于电脑的高速处理能力）。并且，只要保证以其内部每个寄存器均做为一次逻辑锥的顶点来进行逻辑锥的划分，就可以确保在对整个FPGA进行时序分析的时候不留死角。
以上便是形式化验证在FPGA分析时的一种很好的应用。因此，与时序仿真相比，时序分析除了更加简便、省时之外，还绝对的可靠，是现在FPGA项目开发中必不可少的一个环节。

逻辑锥的求解

完成对一个FPGA设计的逻辑锥分解后，接下来的工作就是要去分析每一个逻辑锥是否能够使得其顶点处的寄存器正常工作了。
虽然每个逻辑锥底面的寄存器数目以及椎体的组合逻辑情况都可能千差万别，但是，它们的求解却遵循着同样的原则，即确保顶点处寄存器的建立时间和保持时间满足要求。那么，接下来，就让我们来简单讨论一下，如何进行逻辑锥的求解。

建立时间求解原理

对于一个逻辑锥顶点处的寄存器，其当前时钟有效边沿需要采样的数据，就是其底部寄存器在上一个时钟有效边沿之后输出的数据经由组合逻辑后的运算结果。
如果令时钟周期为T，FPGA芯片的时钟输入pin脚处，两次连续的时钟有效边沿事件分别发生在t_x时刻及t_x+T时刻。
那么，当一切均是理想的时候，即，没有延迟存在的情况下，顶点寄存器的D端口将在t_x时刻得到待采样的稳定数据，而其clk端口将在t_x+T时刻得到进行采样的时钟边沿，此时，顶点寄存器的建立时间为：
tsu = t_x+T -t_x=T
但是，现实世界总是有延迟或异常存在的，从而导致到达顶点寄存器D端口的数据偏差了td，到达顶点寄存器clk端口的时钟边沿偏差了tc，那么，顶点寄存器的建立时间变为：
tsu = （t_x+T+tc）-（t_x+td）=T+tc-td
令寄存器的建立时间要求为Tsurq，那么对于一般情况来说，建立时间满足的不等式为：
T+tc-td≥Tsurq
我们都知道，不等式的成立需要其所包含变量取到所有可能值时均成立才行，但是，除了T之外，上式中其它三个参数都有着共同的联系，这个联系就是温度和电压。因此，我们需要在确定的工况下去分析不等式，否则没有意义。而当工况确定后，Tsurq也就确定了，不等式也可以变为：
tc-td≥(Tsurq-T)
此时，不等式右边是一个常量。那么，如果tc和td是两个变量的话，那么使不等式恒成立的条件就是tc取最小值、td取最大值时，不等式成立。
我们先看tc是否是个变量。虽然在工况确定的时候，门延迟和线延迟便确定了，因此从时钟输入pin脚到该顶点寄存器clk端的延迟时间也就确定了（设其为T_c2pDelay），但是由于时钟信号可能存在jitter（忘记的话请回顾【本篇->基本概念介绍->时钟信号的偏差描述】小节），由于jitter是一个变量，所以tc也可能是个变量，其表达式为：
tc=T_c2pDelay+ t_jitter; |t_jitter |≤T_jitterMax
故
tc_min=T_c2pDelay-T_jitterMax
再来分析td。同样，当时钟信号不存在jitter时，td应该是一个完全由线延迟、门延迟决定的常量，即T_dataDelay。它其实是一条路径的延迟，这条路径的起点仍是时钟输入pin脚，经由逻辑锥底面的寄存器以及逻辑锥内的组合逻辑，最后到达顶点寄存器的D端口。但由于逻辑锥的底面可能有多个寄存器，并且由于组合逻辑的多样性，每个底面寄存器的Q端到顶点寄存器的D端都可能存在多条路径，因此求T_dataDelay本来就是一个复杂的过程。令某条路径的延迟为t_path [i]，则
t_path [i]=T_c2uDelay [x]+Tco+Tcombinational[y]
即，某条路径的延迟等于时钟输入pin脚到其经过的底面寄存器clk端的延迟，加上底面寄存器的Tco，再加上某条从该底面寄存器Q端到顶面寄存器D端的组合逻辑延迟。由于数据稳定取决于延迟最长的那条路径，因此有
T_dataDelay= max┬i⁡〖(t_path [i])〗
上式右边的求解可以利用以递归方式实现的搜索遍历算法求出。接下来，如果再考虑到时钟信号的jitter（jitter是一个相对值，并且由于所有底面寄存器均参考同一个时钟边沿，所以它对每个寄存器都是一样的），可得
td=T_dataDelay+ t_jitter; |t_jitter |≤T_jitterMax
故
td_max=T_dataDelay+T_jitterMax
现在的问题是，t_jitter能否在tc和td中取不同的值？其实是可以的，因为分析tc时，我们考虑的是时钟输入pin脚处t_x+T时刻的有效边沿；而分析td时，我们考虑的是时钟输入pin脚处t_x时刻的有效边沿。由于不是对应于同一个时钟边沿，故它们的jitter没有相关性，可以独立任意取值。因此，考虑到最坏情况，建立时间不等式变为：
T_c2pDelay-T_jitterMax-(T_dataDelay+T_jitterMax)≥(Tsurq-T)
变形为：
T_c2pDelay-T_dataDelay≥(Tsurq-T+2T_jitterMax)
此时，所有参数均为可求解的常量，带入不等式，成立，则说明该逻辑锥在当前工况下的建立时间满足要求；否则，说明该逻辑锥在当前工况下存在问题或隐患。
简单总结一下，逻辑锥的建立时间求解原理，就是要分别针对三种工况，看看到顶点寄存器的D端和clk端同时满足最大数据延迟和最小时钟延迟的时候，该寄存器的建立时间要求是否能够得到满足。
最后，关于建立时间不等式，还有两点需要说明：
1、jitter的问题。考虑到连续两个时钟在时间上离得很近，因此实际工具在计算jitter在底面和顶点寄存器之间引入的最大偏差可能会另选其它估计算法。
2、从整个分析可以看出，t_x与建立时间不等式没有关系，这可以说明两个问题：第一，选取哪两个连续的时钟边沿进行求解是无所谓的；第二，参考时间0点的选取也是无所谓的。由此可见，我们并没有必要在打印分析报告的时候显式的追朔到时钟输入pin脚到不同寄存器的延迟是多少。注意到t_path [i]中有一个分量为T_c2uDelay [x]，故我们只要针对最差情况，给出底面寄存器与顶点寄存器之间的时钟边沿事件到达差（它包含时钟skew以及jitter的综合估计）、底面寄存器的Tco以及组合逻辑延迟Tcombinational[y]即可。

保持时间求解原理

采用与【建立时间求解原理】类似的方法和假设前提，那么，当一切均是理想的时候，即，没有延迟存在的情况下，顶点寄存器的D端口将在t_x时刻得到待采样的稳定数据，该稳定数据将会持续到t_x+T时刻消失（由于新数据的到来），而其clk端口将在t_x+T时刻得到进行采样的时钟边沿，此时，顶点寄存器的保持时间为：
th = t_x+T -(t_x+T)=0
但是，现实世界总是有延迟或异常存在的，从而导致旧数据从顶点寄存器D端口消失的时间偏差了td，到达顶点寄存器clk端口的时钟边沿偏差了tc，那么，顶点寄存器的保持时间变为：
th = （t_x+T+td）-（t_x+T+tc）=td-tc
令寄存器的保持时间要求为Thrq，那么对于一般情况来说，保持时间满足的不等式为：
td-tc≥Thrq
当工况确定后，Thrq也就确定了，所以不等式右边是一个常量。那么，如果td和tc是两个变量的话，那么使不等式恒成立的条件就是td取最小值、tc取最大值时，不等式成立。
同样，对于tc来说，由于jitter的存在，即使是在工况确定的情况下，它也是个变量，其表达式为：
tc=T_c2pDelay+ t_jitter; |t_jitter |≤T_jitterMax
与建立时间不同，这里我们先不忙求出tc的最大值，先去看看td。
同样，当时钟信号不存在jitter时，td应该是一个完全由线延迟、门延迟决定的常量，即T_dataDelay，只不过此时它的表达式应该为：
T_dataDelay= min┬i⁡〖(t_path [i])〗
这是因为数据稳定的开始，取决于路径中最长的那条，但数据稳定的结束，则取决于路径中最短的那条，这也是为什么数据的稳定时间往往都是小于时钟周期T的。
同样，上式右边的求解可以利用以递归方式实现的搜索遍历算法求出（其实对于建立时间和保持时间来说，可以遍历一次同时求出最大最小路径）。接下来，如果再考虑到时钟信号的jitter，可得
td=T_dataDelay+ t_jitter; |t_jitter |≤T_jitterMax
可以看出，导致tc和td变化的均是变量t_jitter。因为旧数据的消失是由于新数据的到来，那么在求解保持时间时，我们关注的是底面寄存器的新值什么时候会导致顶点寄存器D端的旧值发生改变，所以此时，逻辑锥的底面寄存器和顶点寄存器是参考的同一个时钟边沿（t_x+T时刻时钟pin脚处的边沿事件）。由于时钟边沿是同一个，所以它传递到各处的jitter也都是一模一样的，因此在td和tc做差时，jitter的效果就会被抵消掉，这便是为什么保持时间不会受时钟jitter的影响。
因此，保持时间不等式变为：
T_dataDelay+ t_jitter-(T_c2pDelay+ t_jitter)≥Thrq
化简为：
T_dataDelay-T_c2pDelay≥Thrq
此时，所有参数均为可求解的常量，带入不等式，成立，则说明该逻辑锥在当前工况下的保持时间满足要求；否则，说明该逻辑锥在当前工况下存在问题或隐患。
简单总结一下，逻辑锥的保持时间求解原理，就是要分别针对三种工况，在不考虑jitter的前提下，看看到顶点寄存器的D端满足最小数据延迟的时候，该寄存器的建立时间要求是否能够得到满足。
为了区分T_dataDelay在建立时间和保持时间不等式中的不同，我们用T_suDataDelay、T_hDataDelay分别代表，将逻辑锥的建立和保持时间不等式组归纳如下：

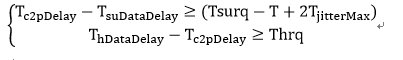
最后，我们同样没有必要在打印分析报告的时候显式的追朔到时钟输入pin脚到不同寄存器的延迟是多少。故我们只要针对T_hDataDelay所对应的路径延迟情况，给出底面寄存器与顶点寄存器之间的时钟边沿事件到达差（它仅需要包含时钟skew，因为jitter是一个共模的干扰变量，做差时自动消除）、底面寄存器的Tco以及对应组合逻辑延迟Tcombinational[y]即可。

一般逻辑锥的求解

前面介绍的逻辑锥，属于比较特例的逻辑锥，因为我们令逻辑锥顶点和底面的所有寄存器均工作于同一个时钟事件下，因此又可称为同步逻辑锥。可事实上逻辑锥在求解的时候只关心时钟事件抵达各个寄存器clk端的时间差，以及逻辑锥中组合逻辑的路径延迟情况，与各个寄存器处敏感的时钟事件是否一致根本无关，因此，只要我们能够知道逻辑锥中驱动不同寄存器的不同时钟事件之间的关系，就可以得到一般逻辑锥的求解思路如下：

一般建立时间求解

在不考虑任何延迟的理想情况下，以逻辑锥顶点处的一次时钟事件为参考，设此时刻为T_top1时刻，那么对于每一个底面寄存器，找到其发生在T_top1时刻之前（不能是T_top1时刻）的最近一次时钟事件T_buttompre1 [n]时刻（T_buttompre1 [n]<T_top1，其中n代表多个底面寄存器）。
则，在考虑了延迟的情况下，令底面寄存器分别受其时钟源端在T_buttompre1 [n]时刻发生时钟事件所驱动输出的值，经过组合逻辑后，传递到顶点寄存器的D端并最终保持稳定的时刻为td；顶点寄存器clk端处收到其源端T_top1时刻时钟事件的时刻为tc；则针对顶点寄存器时钟源端T_top1时刻时钟事件的一般建立时间就等于tc-td。
由于驱动各个寄存器的时钟事件频率可能不尽相同，则tc-td可能会有多个值，所以一般建立时间的求解需要按照上述思路针对顶点寄存器时钟源端多取几个连续的时钟事件（T_top1+n*T_clkTop,n=0,1,2…）分别计算，直到出现重复情况后，再对之前多次的求解结果取最小值，即为该一般逻辑锥的一般建立时间。

一般保持时间求解

在不考虑任何延迟的理想情况下，以逻辑锥顶点处的一次时钟事件为参考，设此时刻为T_top1时刻，那么对于每一个底面寄存器，找到其发生在T_top1时刻之后（可以是T_top1时刻）的最近一次时钟事件T_buttompost1 [n]时刻（T_buttompost1 [n]≥T_top1，其中n代表多个底面寄存器）。
则，在考虑了延迟的情况下，令底面寄存器分别受其时钟源端在T_buttompost1 [n]时刻发生时钟事件所驱动输出的值，经过组合逻辑后，传递到顶点寄存器的D端并开始影响原来旧值稳定的时刻为td；顶点寄存器clk端处收到其源端T_top1时刻时钟事件的时刻为tc；则针对顶点寄存器时钟源端T_top1时刻时钟事件的一般保持时间就等于td-tc。
由于驱动各个寄存器的时钟事件频率可能不尽相同，则td-tc可能会有多个值，所以一般保持时间的求解需要按照上述思路针对顶点寄存器时钟源端多取几个连续的时钟事件（T_top1+n*T_clkTop,n=0,1,2…）分别计算，直到出现重复情况后，再对之前多次的求解结果取最小值，即为该一般逻辑锥的一般保持时间。

文章来源: reborn.blog.csdn.net，作者：李锐博恩，版权归原作者所有，如需转载，请联系作者。

原文链接：reborn.blog.csdn.net/article/details/105104731