前言

本文摘自《FPGA之道》。

功能仿真篇

功能仿真是所有仿真类型中最重要的，也是占项目开发比重最大的仿真，对任何一个项目的开发来说几乎都是必须的，所以在此单独使用一个篇章对它进行介绍。因此，本篇所指的“仿真”若无特别说明，皆泛指功能仿真。

仿真原理

功能仿真是FPGA项目开发中重要的一环，它是确保我们编写的HDL设计代码在功能上准确无误的重要方法。FPGA中的电路都是并发执行的，因此HDL语言的本质也是并行的，并且硬件电路是无时无刻不在工作的。可FPGA的功能仿真是基于PC机上的相关软件仿真环境的，而PC机上软件的执行思路都是串行的，并且PC机每秒的运算次数是有限的。那么想以串行模仿并行，以有限模仿无限，是否可行？它的原理又是什么？这就是我们本章节需要讨论的问题。

串行模仿并行思路分析

串行模仿并行主要分为两种情况：

一、独立的并行电路
若并行的电路之间是相互独立的，那么此时，同时开始做N件事和做完一件事再开始下一件事从结果上来看是完全一样的。例如加法器1的输入是A和B，输出是C，加法器2的输入是D、E，输出是F，如下图：

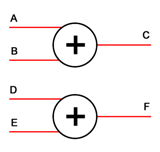
此时无论是找两个人分别同时计算两个加法器的输出结果还是只找一个人按任意顺序逐个计算两个加法器的输出结果，最终得到的答案都会是一样的。因此这种情况下串行可以比较轻松的模拟并行。

二、有关联的并行电路
若并行的电路之间不是相互独立的，那么此时，情况就不那么简单了。例如，加法器1的输入是A和B，输出是C，加法器2的输入是C、D，输出是E，如下图：

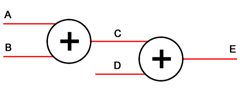
这个时候，由于模拟环境会保留电路上一次模拟后的结果，所以先计算加法器1还是加法器2，得到的结果是不同的，并且此时并行的模拟思路如果只做一次的话，也无法给出正确的结果。因此这种情况下，串行要想正确的模拟并行，需要遵循正确的执行顺序。
分析到这里，我想大家应该对HDL中设置串行执行的子语句体的用意有新的看法了吧。而且，为了配合得出正确的仿真结果，我们在串行子语句体中最好能够严格按照数字信号传递的方向书写代码。

有限模仿无限思路分析

硬件电路只要一上电，就会持续不断的工作，永不停歇，因为现实中的电信号时间上都是连续的。而软件的计算都是离散的，即使令仿真的时间间隔趋近于无穷小，这样虽然可以使仿真情况无限逼近真实情况，但是却仍不能完全代替真实情况，并且从计算量上来看，也是无法完成的。因此以PC有限的计算能力仿真硬件无限的时间变化，不能简单的利用高频率的采样来解决。
那么，仍以一个加法器为例来分析，设加法器的输入为A和B，输出为C，如下图：

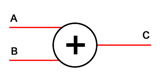
若一开始，令A等于5，B等于3，那么C自然应该等于8。若这种情况持续了10秒钟，那么，在这10秒钟之内，由于A和B的值都没有改变，虽然加法器电路在一直工作，而且也经过了无数次的加法运算，可是由于每次计算出的C值都为8，因此输出也一直没有改变。如果在这之后，A的值变为7，那么加法器的输出C会迅速变为10，并且此后C的值会一直保持下去，直到A或B的下一次变化到来，C才有可能改变（因为若A变为8，B变为2，C仍应该为10）。写到这里，我想大家应该明白了，虽然硬件电路无时无刻不在进行运算，但是，只有那些可能会改变输出的运算才是最重要的，只要能够捕捉住这些关键时刻，就可以完全模拟出真实的情况。因此，利用这一思路，就可以在FPGA中用有限来模拟无限了。
分析到这里，我想大家对HDL中的敏感量表应该有了新的认识吧。而且，为了配合得出正确的仿真结果，我们往往需要给出正确的敏感量表，虽然目前来说这对实际硬件电路的实现已经几乎没有影响了。

组合逻辑仿真原理

组合逻辑的仿真原理就是结合上面分析的两种思路得来的，我们姑且称这两种思路为“化并行为串行”和“化无限为有限”。因此，只要注意合理的语句顺序安排和正确的敏感量表提取，就可以实现正确和高效的组合逻辑功能仿真。

时序逻辑仿真原理

时序逻辑中最重要的就是寄存器。我们以一个最基本的上升沿敏感的寄存器为例来讨论，它有三个最重要的端口，分别是两个输入端口CLK、D，一个输出端口Q。它的功能可以描述为：无论输入端口D的值怎么变化，当且仅当CLK的上升沿到来的时刻，更新输出端口Q的值为此时输入端口D的值。此后端口Q的值将会保持下去，直到下一次CLK的上升沿到来才有可能更新（D的值也许和上次一样，这样更新了也看不出来）。
因此，虽然寄存器内部的电路是一直工作的，而且随着D值的变化，寄存器内部的部分电路的值也是不断在变化的，可是由于在任意两个连续的clk上升沿期间，Q值绝对不会变化，所以我们可以仅仅保留CLK的上升沿时刻作为关键时刻，来化无限为有限，从而得出正确的仿真结果。
分析到这里，我想大家对HDL中的时序描述程序段中的敏感量表的意义也会有进一步的认识了吧。
上述分析只解决了“化无限为有限”的问题，那么如果时序逻辑中需要同时改变多个寄存器的值的时候，该怎么得出正确的仿真结果呢？由于时序逻辑的赋值在物理硬件上是有一定延迟的，因此，对多个寄存器在进行并行赋值的时候，情况要比组合逻辑简单的多，那是因为所有寄存器在赋值的时侯，新值并不是立即生效，而是等所有的寄存器赋值语句都执行后的某一个时刻才生效。根据这样的道理，那么“化并行为串行”就是很简单的事情，因为连赋值语句的书写顺序都是无所谓的了。不过，为了提高代码的阅读性，便于以后的分析和修改，我还是建议大家“尽量”按照数字信号的传递方向来书写时序逻辑代码。说“尽量”，是因为在有些情况下，严格按照数字信号的传递方向来书写时序逻辑代码是不可能的，例如循环移位寄存器。

HDL的仿真原理

初学HDL语法的时候，都会对HDL语法中的串行、并行、敏感量表等定义多多少少有些费解。甚至在从事FPGA开发的初期，由于编写的逻辑功能过于简单，发现即使不严格按照语法规定的要求来做也一样能够在FPGA中实现正确的逻辑功能。这是因为编译器会对我们的HDL代码进行分析、补充、修改和优化，从而用最接近的门级电路来实现HDL代码所描述的功能。但是，还是请大家养成严格遵守语法要求的编程习惯！首先，编译器并不是每次都能帮你把电路适配正确的。其次，仿真器不具有将HDL代码转换为电路的功能，它只能严格按照语法来理解我们的HDL代码。所以，HDL语法对于仿真器是很重要的，它是仿真器理解FPGA设计的“新华字典”，要想使自己的HDL代码得到正确仿真，在最开始编写HDL代码的时候，就要养成严格遵守HDL语法的好习惯！
通过之前的讨论，我们可以断定，只要有合理的语句顺序安排（对于时序逻辑这点甚至也是可以不需要的）和正确的敏感量表提取，我们就能完美的仿真VHDL中的process语句体，或者Verilog中的always程序块。但是HDL语法中有还有很多其他的语法结构，它们该怎么仿真呢？
先看【程序设计篇->编程语法->VHDL基本语法->VHDL基本程序框架】小节介绍的VHDL基本模板，除去一些与功能无关的端口声明、变量声明等以外，具有功能描述的部分除了process就剩元件例化语句和独立赋值语句了。在介绍VHDL基本程序框架时，我们分析过，architecture中的独立语句其实就相当于只有一条代码的纯组合逻辑process。而元件例化语句所调用元件的功能，最终其实也是对应到该元件architecture中描述的process、元件例化或者独立语句。因此，VHDL中所有的并行语句都可以很方便的直接或间接的转换为process语句结构。那么此时，只要利用“化并行为串行”和“化无限为有限”的思想，VHDL语言即是可仿的。
对于【程序设计篇->编程语法->Verilog基本语法->Verilog基本程序框架】小节中介绍的Verilog基本模板的分析也是一样。Verilog中所有的功能性并行语句都可以直接或间接转换为always程序块，因此利用“化并行为串行”和“化无限为有限”的思想，Verilog语言也是可仿的。

仿真时间与物理时间

仿真时间就是指仿真器模拟了FPGA芯片在现实世界中多少时间的工作行为，而物理时间指的是仿真过程所消耗的现实世界的时间长度。两者的概念是截然不同的，举例如下：
如果FPGA芯片中实现的功能原理图如下：

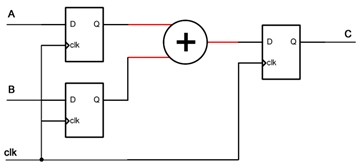
其时钟的频率为10MHz，那么在现实世界中，该FPGA芯片在一秒钟之内可以依次、串行的完成1千万次加法运算。
如果本次仿真仅需要仿真1亿次加法，那么整个仿真过程完成的仿真时间为(1亿次/1千万次) 1秒 = 10秒，即仿真器仿真了1亿次加法，相当于模仿了FPGA芯片在现实世界中10秒钟时间内的工作行为。
同样是仿真1亿次加法，如果你使用的计算机每完成一次加法的模拟需要10个指令周期（包括读取新的加数、被加数，计算加法，输出结果等等操作），而你使用的计算机每个指令周期为1纳秒，那么整个仿真过程消耗的物理时间为(1亿次10指令周期每次1纳秒)=1秒，即你只需要坐在你的电脑前，等待1秒钟，就可以看到FPGA芯片在现实世界中需要10秒钟才能完成的所有行为。不过请注意，物理时间是与你所使用的计算机的性能息息相关的，如果你有一台高性能的电脑，可能等待的时间就变为0.1秒，如果你用的是一台老古董，等待的时间很可能变为3秒、4秒甚至更多。
仿真1亿次加法，完成仿真时间10秒，而消耗物理时间1秒，初步看来仿真效率还蛮高的，不过请不要高兴得太早，现实情况中往往不是这样的，因为FPGA设计最大的特点就是其并行性。对于稍微复杂一点的FPGA设计，它每秒完成的运算恐怕就是1千万次并行算子。如果一个并行算子的复杂度是加法的1万倍，那么仿真一个并行算子很可能就需要10万个指令周期。此时仿真1亿次该并行算子所消耗的物理时间为(1亿次10万指令周期每次*1纳秒)=1万秒≈3小时，即为了完成10秒钟的仿真时间，你可能需要痴痴地在电脑前等上3个小时，这种情况下我还是建议你先去买包瓜子吧！
因此，在通常的仿真调试环节，我们一般将仿真时间设定的比较短，这样可以控制物理时间在分钟级别，从而方便调试工作的开展。不过为了提高仿真的充分性，我们一般会跑上一、两次消耗物理时间比较长的仿真。

文章来源: reborn.blog.csdn.net，作者：李锐博恩，版权归原作者所有，如需转载，请联系作者。

原文链接：reborn.blog.csdn.net/article/details/105509737