机器学习3-训练与损失

​前言

训练模型表示通过有标签样本学习模型中所有权重w和偏差b的最优值。在监督学习中，机器学习算法通过以下方式构建模型：检查多个样本并尝试找出可最大限度地减少模型的损失；这一过程称为经验风险最小化。

损失是对糟糕预测的惩罚；损失是之歌数值，表示对个单个样本而言模型预测的准确程度。如果模型的预测完成准确，则损失为零，否则损失会较大。

训练模型

训练模型的目标是从所有样本中找到一组平均损失“较少”的权值和偏差。

​

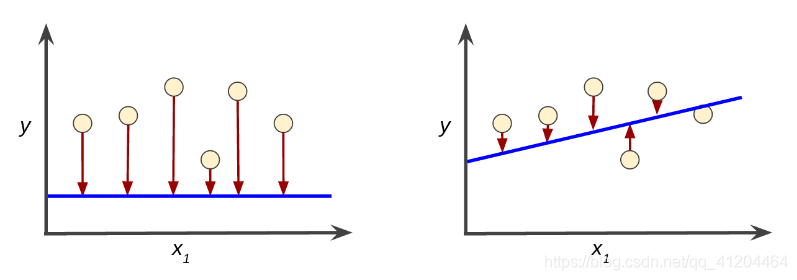
红色箭头表示损失；蓝线表示预测。左侧曲线图中的红色箭头比右侧曲线图中的对应红色箭头长得多；即实际点和模型预测相差的距离比较远，差异更大。

左侧显示的是损失较大的模型；右侧显示的是损失较小的模型。

损失函数

平方损失是一种常见的损失函数。线性回归模型使用的是一种称为平方损失（又称​损失）的损失函数。单个样本的平方损失如下：

  = the square of the difference between the label and the prediction
  = (observation - prediction(x))2
  = (y - y')2

均方误差（MSE）是指每个样本的平均平方损失。计算MSE，需要求出各个样本的所有平方损失之和，然后除以样本数量：

​

其中：

• (x,y)是指样本；x是指模型进行预测时使用的特征集（比如：温度、年龄等）y是指样本的标签（比如：蟋蟀每分钟的鸣叫次数）
• prediction（x）是指权重和偏差与特征集x结合的函数。
• D是指包含多个有标签样本的数据集。
• n是指D中的样本数量。

MSE常用语回归任务中；分类任务常用交叉熵损失函数。

参考：https://developers.google.cn/machine-learning/crash-course/descending-into-ml/training-and-loss

关键词

经验风险最小化（ERM，empirical risk minimization），用于选择函数，选择基于训练集的损失降至最低的函数。与结构风险最小化相对。

均方误差（MSE，Mean Squared Error），每个样本的平均平方损失。MSE的计算方法是平方损失除以样本数。

平方损失函数（squared loss）在线性回归中使用的损失函数（也称为L2损失函数）。改行可计算模型为有标签样本预测的值，和标签的真实值之差的平方。   由于取平方值，该损失函数会放大不佳预测的影响。与L1损失函数相对，平方损失函数对离群值的反应更强烈。

训练（training）构建模型的理想参数的过程。

损失（Loss）一种衡量指标，用于衡量模型的预测偏离其标签程度。要确定此值，模型需要定义损失函数。例如：线性回归模型参与均方误差MAS损失函数，分类模型采用交叉熵损失函数。

​