Opencv C++ 归一化
c++默认是uint8,uchar类型,归一化需要数据转换,在3.4.8版本下,没有试验成功
在3.4.8版本下,先转换类型,再进行除法操作,也没试验成功。
这个可以:文章后面有3通道分别归一化:
-
Mat img = cv::imread("bar1.jpg");
-
-
img.convertTo(img, CV_32FC1);
-
-
normalize(img, img, 1.0, 0.0, NORM_MINMAX);
-
-
cout << img << endl;
后面有vector<double>的成功了,
可能是最后transpose没有做,导致的失败?
1.函数原型
void cv::normalize(InputArry src,InputOutputArray dst,double alpha=1,double beta=0,int norm_type=NORM_L2,int dtype=-1,InputArray mark=noArry())
2.函数作用
归一化数据。该函数分为范围归一化与数据值归一化。(Normalizes the norm or value range of an array.)
3.参数说明
src 输入数组;
dst 输出数组,数组的大小和原数组一致;
alpha 1,用来规范值,2.规范范围,并且是下限;
beta 只用来规范范围并且是上限;
norm_type 归一化选择的数学公式类型;
dtype 当为负,输出在大小深度通道数都等于输入,当为正,输出只在深度与输如不同,不同的地方游dtype决定;
mark 掩码。选择感兴趣区域,选定后只能对该区域进行操作。
4.归一化选择的数学公式类型介绍(norm_type)
设数组中原有{A1,A2,A3...An}
NORM_L1:
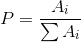
NORM_INF:
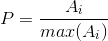
NORM_L2:

NORM_MINMAX:(AK不属于{max(Ai)},min(Ai),当AK等于max(Ai)时p=1,等于min(Ai)时p=0)
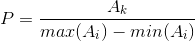
6.范围归一化与值归一化的区别
区别一:范围归一化使用的是如下式子,设范围为【0,255】
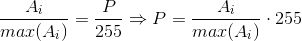
即把src缩放到【0,255】这个范围内,并不使用上面的4个公式去解。
区别二:使用范围归一化时,beta必有值不等于0
举例说明:
一 值归一化:
-
#include<opencv2/opencv.hpp>
-
-
#include<iostream>
-
-
using namespace std;
-
-
int main()
-
-
{
-
-
vector<double>a={ 10,11,234,45,65,456,0 };
-
-
cv::normalize(a, a, 1,0, cv::NORM_MINMAX);
-
-
for (int i=0;i < a.size();i++)
-
-
{
-
-
cout << a[i] << endl;
-
-
}
-
-
return 0;
-
-
}
结果如下:
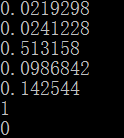
二 范围归一化
-
#include<opencv2/opencv.hpp>
-
-
#include<iostream>
-
-
using namespace std;
-
-
int main()
-
-
{
-
-
vector<double>a={ 10,11,234,45,65,456,0 };
-
-
cv::normalize(a, a, 0,255, cv::NORM_MINMAX);
-
-
for (int i=0;i < a.size();i++)
-
-
{
-
-
cout << a[i] << endl;
-
-
}
-
-
return 0;
-
-
}
结果如下:

Opencv C++下的Mat归一化
void Mat_L2_mormal(cv::Mat &image)
{
//mat*mat,
cv::Mat out;
out=(image) .mul (image);
float sum=0.0;
for (int i=0;i<image.rows;i++){
sum=sqrt(cv::sum(out.row(i))[0]);
image.row(i)=(image.row(i)/sum);
}
out.release();
}
-
float scale = 0.0078125f ;
-
float mean_value = 127.5f;
-
-
void Mat_L2_mormal(cv::Mat &image)
-
{
-
for (int i = 0; i<image.rows; i++)
-
{
-
for (int j = 0; j<image.cols; j++)
-
{
-
image.at<Vec3b>(i, j)[0] = (image.at<Vec3b>(i, j)[0] - mean_value) * scale;
-
image.at<Vec3b>(i, j)[1] = (image.at<Vec3b>(i, j)[1] - mean_value) * scale;
-
image.at<Vec3b>(i, j)[2] = (image.at<Vec3b>(i, j)[2] - mean_value) * scale;
-
}
-
}
-
-
}
-
-
//方法2
-
-
double minv = 0.0, max_v = 0.0;
-
minMaxIdx(image1, &minv, &maxv);
-
-
-
for (int row = 0; row < face_img.rows; row++)
-
{
-
for (int col = 0; col < face_img.cols; col++)
-
{
-
for (int k = 0; k < 3; k++) {
-
const auto src = face_img.at<cv::Vec3b>(row, col)[k];
-
auto dst = 0.0;
-
-
if (k == 0) dst = ((float(src) / max_v - 0.485) / 0.229) ;
-
if (k == 1) dst = ((float(src) / max_v - 0.456) / 0.224) ;
-
if (k == 2) dst = ((float(src) / max_v - 0.406) / 0.225) ;
-
inputData[k * resize_w * resize_h + row * resize_w + col] = dst;
-
}
-
}
-
}
二、深度转换–convertTo()
2.1、API介绍
void convertTo( OutputArray dst, int rtype, double alpha=1, double beta=0 )
1
参数dst:输出图像;
参数rtype:要转换的深度;
参数alpha:对灰度值的缩放倍数;
参数beta:对灰度值得增量。
公式: dst = satyrate_cast(src * alpha + beta);
这个也是减均值128,归一化
-
cv::cvtColor(imgResized, imgResized, cv::COLOR_RGB2BGR);
-
-
//Mat_L2_mormal(imgResized);
-
vector<Mat> bgr;
-
cv::split(imgResized, bgr);
-
bgr[0].convertTo(bgr[0], CV_32F, 1.f / 128.f, -1.f);
-
bgr[1].convertTo(bgr[1], CV_32F, 1.f / 128.f, -1.f);
-
bgr[2].convertTo(bgr[2], CV_32F, 1.f / 128.f, -1.f);
文章来源: blog.csdn.net,作者:网奇,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/jacke121/article/details/106175928
- 点赞
- 收藏
- 关注作者


评论(0)