贝叶斯定理

搞数理统计如果不知道贝叶斯定理，那么你的人生肯定是不完整的。贝叶斯定理是贝叶斯推断的应用，是英国数学家托马斯·贝叶斯在1763年首次提出的。与其他统计学不同，贝叶斯定理是建立在主观判断的基础上，它需要有大量的样本数据，并在数据的基础上进行计算，数据量越大，计算结果越能反映现实世界。

在计算机诞生之前，这个前提条件是很难满足的，所以贝叶斯定理在历史上很长一段时间内都没有得到很好的应用。然后，互联网时代来临了……

现在贝叶斯定理广泛应用于中文分词、垃圾邮件处理、机器学习、图像识别、拼写检查和一些常用的分类算法上。可以说，我们现在最常用的互联网服务上，贝叶斯定理无处不在

定义

贝叶斯定理是关于随机事件 A 和 B 的条件概率：

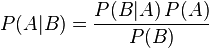
其中P(A|B)是在 B 发生的情况下 A 发生的可能性。

在贝叶斯定理中，每个名词都有约定俗成的名称：

  

   

    

     

    
    

     

      P(A)是 A 的先验概率，之所以称为“先验”是因为它不考虑任何 B 方面的因素。
     
    
   

    

     

    
    

     

      P(A|B)是已知 B 发生后 A 的条件概率，也由于得自 B 的取值而被称作 A 的后验概率。
     
    
   

    

     

    
    

     

      P(B|A)是已知 A 发生后 B 的条件概率，也由于得自 A 的取值而被称作 B 的后验概率。
     
    
   

    

     

    
    

     

      P(B)是 B 的先验概率，也作标淮化常量（normalizing constant）。
     
    
  
 

按这些术语，贝叶斯定理可表述为：

后验概率 = (相似度 * 先验概率)/标淮化常量

 

也就是说，后验概率与先验概率和相似度的乘积成正比。

另外，比例P(B|A)/P(B)也有时被称作标淮相似度（standardised likelihood），Bayes定理可表述为：

后验概率 = 标淮相似度 * 先验概率

 

条件概率就是事件 A 在另外一个事件 B 已经发生条件下的发生概率。条件概率表示为P(A|B)，读作“在 B 发生的条件下 A 发生的概率”。

联合概率表示两个事件共同发生（数学概念上的交集）的概率。A 与 B 的联合概率表示为。

推导

我们可以从条件概率的定义推导出贝叶斯定理。

根据条件概率的定义，在事件 B 发生的条件下事件 A 发生的概率为：

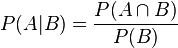
同样地，在事件 A 发生的条件下事件 B 发生的概率为：

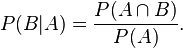
结合这两个方程式，我们可以得到：

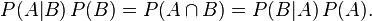
这个引理有时称作概率乘法规则。上式两边同除以 P(A)，若P(A)是非零的，我们可以得到贝叶斯定理:

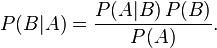
解释

通常，事件 A 在事件 B 发生的条件下的概率，与事件 B 在事件 A 发生的条件下的概率是不一样的；然而，这两者是有确定关系的，贝叶斯定理就是这种关系的陈述。

贝叶斯公式的用途在于通过己知三个概率来推测第四个概率。它的内容是：在 B 出现的前提下，A 出现的概率等于 A 出现的前提下 B 出现的概率乘以 A 出现的概率再除以 B 出现的概率。通过联系 A 与 B，计算从一个事件发生的情况下另一事件发生的概率，即从结果上溯到源头（也即逆向概率）。

通俗地讲就是当你不能确定某一个事件发生的概率时，你可以依靠与该事件本质属性相关的事件发生的概率去推测该事件发生的概率。用数学语言表达就是：支持某项属性的事件发生得愈多，则该事件发生的的可能性就愈大。这个推理过程有时候也叫贝叶斯推理。

例子：

文章来源: blog.csdn.net，作者：网奇，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/jacke121/article/details/54885242