反向传播算法（过程及公式推导）
【摘要】
反向传播算法（Backpropagation）是目前用来训练人工神经网络（Artificial Neural Network，ANN）的最常用且最有效的算法。其主要思想是：
（1）将训练集数据输入到ANN的输入层，经过隐藏层，最后达到输出层并输出结果，这是ANN的前向传播过程；
（2）由于ANN的输出结果与实际结果有误差，则计算估计值与实际值...
反向传播算法（Backpropagation）是目前用来训练人工神经网络（Artificial Neural Network，ANN）的最常用且最有效的算法。其主要思想是：
（1）将训练集数据输入到ANN的输入层，经过隐藏层，最后达到输出层并输出结果，这是ANN的前向传播过程；
（2）由于ANN的输出结果与实际结果有误差，则计算估计值与实际值之间的误差，并将该误差从输出层向隐藏层反向传播，直至传播到输入层；
（3）在反向传播的过程中，根据误差调整各种参数的值；不断迭代上述过程，直至收敛。
反向传播算法的思想比较容易理解，但具体的公式则要一步步推导，因此本文着重介绍公式的推导过程。
1. 变量定义
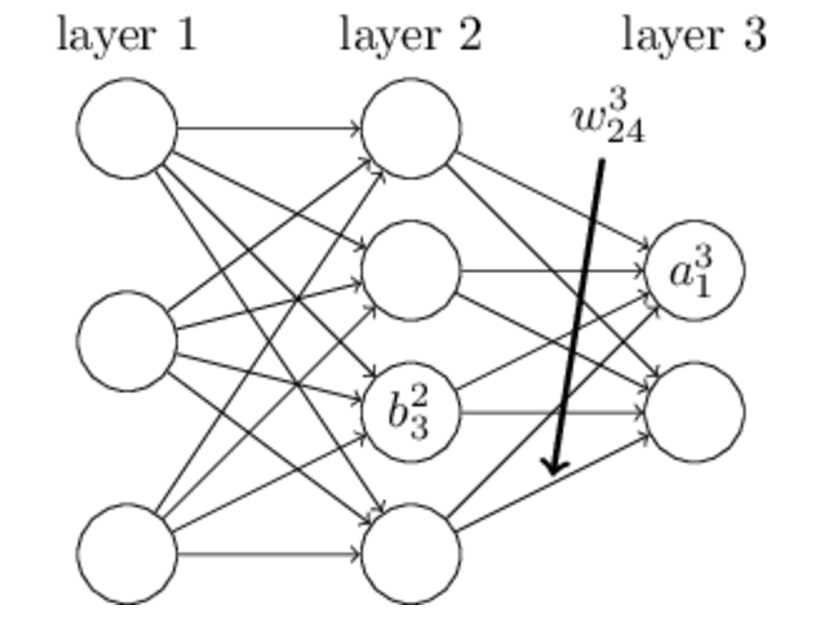
上图是一个三层人工神经网络，layer1至layer3分别是输入层、隐藏层和输出层。如图，先定义一些变量：
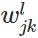表示第
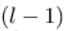
层的第
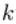个神经元连接到第
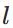层的第
个神经元的权重；
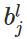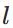表示第层的第个神经元的偏置；
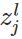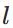表示第层的第个神经元的输入，即：
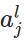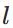
表示第层的第个神经元的输出，即：
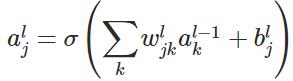
其中表示激活函数。
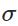
表示激活函数。
2. 代价函数
代价函数被用来计算ANN输出值与实际值之间的误差。常用的代价函数是二次代价函数（Quadratic cost function）：
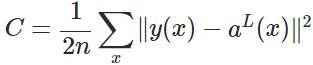
其中，表示输入的样本，表示实际的分类，表示预测的输出，表示神经网络的最大层数。
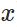
表示输入的样本，
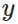表示实际的分类，
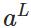表示预测的输出，
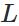表示神经网络的最大层数。
3. 公式及其推导
本节将介绍反向传播算法用到的4个公式，并进行推导。如果不想了解公式推导过程，请直接看第4节的算法步骤。
首先，将第层第个神经元中产生的错误（即实际值与预测值之间的误差）定义为：
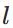
层第个神经元中产生的错误（即实际值与预测值之间的误差）定义为：
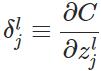
本文将以一个输入样本为例进行说明，此时代价函数表示为：
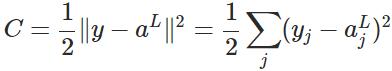
公式1（计算最后一层神经网络产生的错误）：
其中，表示Hadamard乘积，用于矩阵或向量之间点对点的乘法运算。 公式1的推导过程如下：
表示Hadamard乘积，用于矩阵或向量之间点对点的乘法运算。 公式1的推导过程如下：
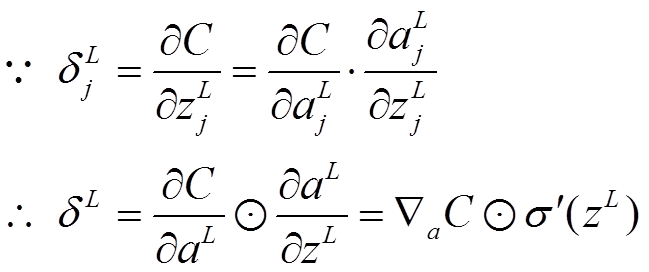
公式2（由后往前，计算每一层神经网络产生的错误）：
推导过程：
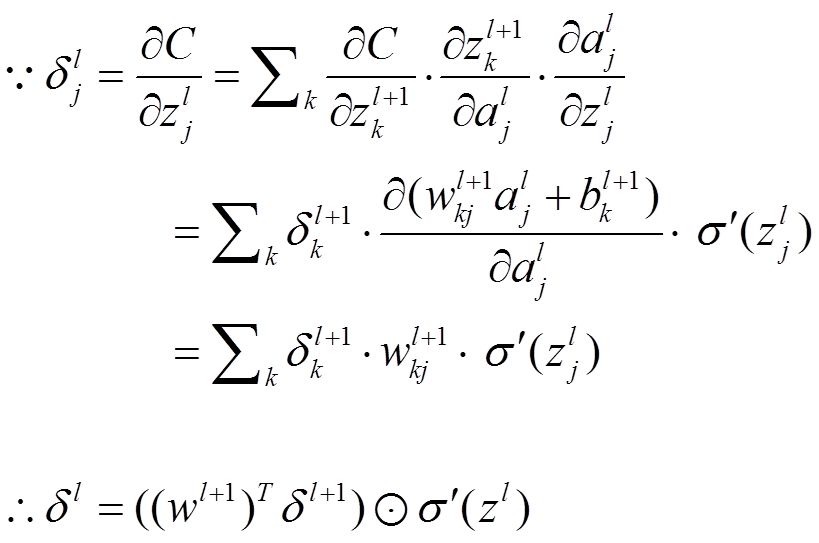
公式3（计算权重的梯度）：
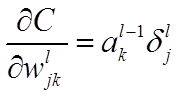
推导过程：
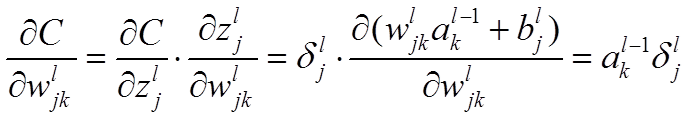
公式4（计算偏置的梯度）：
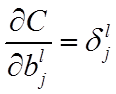
推导过程：
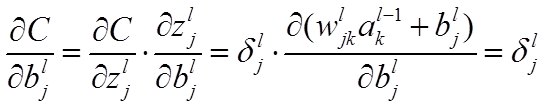
4. 反向传播算法伪代码
- 输入训练集
- 对于训练集中的每个样本x，设置输入层（Input layer）对应的激活值：
- 前向传播：
：
， 
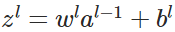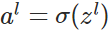
- 计算输出层产生的错误：
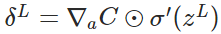
- 反向传播错误：
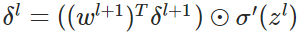
- 使用梯度下降（gradient descent），训练参数：
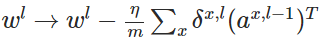
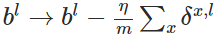
文章来源: blog.csdn.net，作者：网奇，版权归原作者所有，如需转载，请联系作者。
原文链接：blog.csdn.net/jacke121/article/details/54935021
【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱：
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者
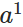评论（0）