KCF高速跟踪详解

思想

一般化的跟踪问题可以分解成如下几步：
1. 在帧中，在当前位置附近采样，训练一个回归器。这个回归器能计算一个小窗口采样的响应。
2. 在帧中，在前一帧位置附近采样，用前述回归器判断每个采样的响应。
3. 响应最强的采样作为本帧位置。

循环矩阵表示图像块

在图像中，循环位移操作可以用来近似采样窗口的位移。

训练时，围绕着当前位置进行的一系列位移采样可以用二维分块循环矩阵表示，第ij块表示原始图像下移i行右移j列的结果。类似地，测试时，前一帧结果附近的一系列位移采样也可以用表示。

注意：这里是分块循环矩阵，不是循环矩阵，

在线性代数中，循环矩阵是一种特殊形式的 Toeplitz矩阵，它的行向量的每个元素都是前一个行向量各元素依次右移一个位置得到的结果。由于可以用离散傅立叶变换快速解循环矩阵，所以在数值分析中有重要的应用。

a=[1 2 3 3 1 2 2 3 1;
4 5 6 6 4 5 5 6 4;
7 8 9 9 7 8 8 9 7;
7 8 9 9 7 8 8 9 7;
1 2 3 3 1 2 2 3 1;
4 5 6 6 4 5 5 6 4;
4 5 6 6 4 5 5 6 4;
7 8 9 9 7 8 8 9 7;
1 2 3 3 1 2 2 3 1;
]

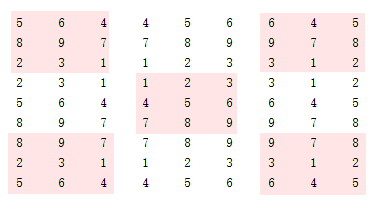
这样的可以利用傅里叶变换快速完成许多线性运算。

线性回归训练提速

此部分频繁用到了循环矩阵的各类性质，请参看这篇博客。
线性回归的最小二乘方法解为：

根据循环矩阵乘法性质，的特征值为。本身就是一个循环矩阵，其生成向量为，这个生成向量的傅里叶变换为全1向量，记为。

根据循环矩阵求逆性质，可以把矩阵求逆转换为特征值求逆。

利用的酉矩阵性质消元：

分号表示用1进行对位相除。
反用对角化性质：，上式的前三项还是一个循环矩阵。

利用循环矩阵卷积性质：

论文中，最后这一步推导的分子部分写成，是错误的。但代码中没有涉及。

线性回归系数可以通过向量的傅里叶变换和对位乘法计算得到。

核回归训练提速

不熟悉核方法的同学可以参看这篇博客的简单说明。核回归方法的回归式为：

为所有训练样本的核相关矩阵：。如果核函数选择得当，使得内部元素顺序更换不影响核函数取值，则可以保证也是循环矩阵。以下核都满足这样的条件：

设核相关矩阵的生成向量是。推导和之前线性回归的套路非常类似：

利用循环矩阵卷积性质：

两者都是同一个向量和自身位移结果进行运算。因为所有涉及到的核函数都只和位移的绝对值有关，所以，即是对称向量。

举例：，，。使用多项式核，容易验证。

对称向量的傅里叶变换为实数，有：

论文中，利用的对称性消除共轭的步骤没有提及。

线性回归系数可以通过向量的傅里叶变换和对位乘法计算得到。

核回归检测提速

所有待检测样本和所有训练样本的核相关矩阵为，每一列对应一个待测样本。可以一次计算所有样本的响应（向量）：

利用循环矩阵的转置性质性质，的特征值为：

利用循环矩阵的卷积性质：

两边傅里叶变换：

论文中，利用转置消除共轭的步骤没有提及。

所有侯选块的检测响应可以通过向量的傅里叶变换和对位乘法计算得到。

核相关矩阵计算提速

无论训练还是检测，都需要计算核相关矩阵的生成向量。除了直接计算每一个核函数，在某些特定的核函数下可以进一步加速。

多项式核

其中为多项式函数。写成矩阵形式：

在矩阵的每个元素上单独进行。根据循环矩阵性质，也是一个循环矩阵，其生成向量为。所以核相关矩阵的生成向量为：

RBF核

其他核

有一些核函数，虽然能保证是循环矩阵，但无法直接拆解出其特征值，快速得到生成向量。比如Hellinger核：，Intersection核：。

多通道

在多通道情况下（例如使用了HOG特征），生成向量变成，其中是样本像素数，是特征维度。在上述所有计算中，需要更改的只有向量的内积：

注：非常感谢GX1415926535和大家的帮助，发现原文一处错误。(21)式中不应有转置，应为：

文章来源: blog.csdn.net，作者：网奇，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/jacke121/article/details/62891960