K-means算法、高斯混合模型

简介：

        本节介绍STANFORD机器学习公开课中的第12、13集视频中的算法：K-means算法、高斯混合模型（GMM）。（9、10、11集不进行介绍，略过了哈）

一、K-means算法

        属于无监督学习的聚类算法，给定一组未标定的数据（输入样本），对其进行分类，假设可分为k个类。由于算法比较直观，故直接给出步骤和MATLAB代码。（k-means算法在数学推导上是有意义的）

MATLAB代码：

[cpp] view plain copy

print ?

1. %%  
2. %k均值聚类  
3. clear all;  
4. close all;  
5. %%  
6. n=2;  
7. m=200;  
8. v0=randn(m/2,2)-1;  
9. v1=randn(m/2,2)+1;  
10. figure;  
11. subplot(221);  
12. hold on;  
13. plot(v0(:,1),v0(:,2),'r.');  
14. plot(v1(:,1),v1(:,2),'b.');  
15. %axis([-5 5 -5 5]);  
16. title('已分类数据');  
17. hold off;  
18.   
19. data=[v0;v1];  
20. data=sortrows(data,1);  
21. subplot(222);  
22. plot(data(:,1),data(:,2),'g.');  
23. title('未分类数据');  
24. %axis([-5 5 -5 5]);  
25. %%  
26. [a b]=size(data);  
27. m1=data(20,:);%随机取重心点  
28. m2=data(120,:);%随机取重心点  
29. k1=zeros(1,2);  
30. k2=zeros(1,2);  
31. n1=0;  
32. n2=0;  
33. subplot(223);hold on;  
34. %axis([-5 5 -5 5]);  
35. for t=1:10  
36.     for i=1:a  
37.         d1=pdist2(m1,data(i,:));  
38.         d2=pdist2(m2,data(i,:));  
39.         if (d1<d2)  
40.             k1=k1+data(i,:);  
41.             n1=n1+1;  
42.             plot(data(i,1),data(i,2),'r.');  
43.         else  
44.             k2=k2+data(i,:);  
45.             n2=n2+1;  
46.             plot(data(i,1),data(i,2),'b.');  
47.         end  
48.     end  
49.     m1=k1/n1;  
50.     m2=k2/n2;  
51. %     plot(m1(1,1),m1(1,2),'g.');  
52. %     plot(m2(1,1),m2(1,2),'g.');  
53.     k1=zeros(1,2);  
54.     k2=zeros(1,2);  
55.     n1=0;  
56.     n2=0;  
57. end  
58. plot(m1(1,1),m1(1,2),'k*');  
59. plot(m2(1,1),m2(1,2),'k*');  
60. title('k-means聚类');  
61. hold off;  

        %%
        %k均值聚类
        clear all;
        close all;
        %%
        n=2;
        m=200;
        v0=randn(m/2,2)-1;
        v1=randn(m/2,2)+1;
        figure;
        subplot(221);
        hold on;
        plot(v0(:,1),v0(:,2),'r.');
        plot(v1(:,1),v1(:,2),'b.');
        %axis([-5 5 -5 5]);
        title('已分类数据');
        hold off;
        data=[v0;v1];
        data=sortrows(data,1);
        subplot(222);
        plot(data(:,1),data(:,2),'g.');
        title('未分类数据');
        %axis([-5 5 -5 5]);
        %%
        [a b]=size(data);
        m1=data(20,:);%随机取重心点
        m2=data(120,:);%随机取重心点
        k1=zeros(1,2);
        k2=zeros(1,2);
        n1=0;
        n2=0;
        subplot(223);hold on;
        %axis([-5 5 -5 5]);
        for t=1:10
        for i=1:a
         d1=pdist2(m1,data(i,:));
         d2=pdist2(m2,data(i,:));
        if (d1<d2)
         k1=k1+data(i,:);
         n1=n1+1;
         plot(data(i,1),data(i,2),'r.');
        else
         k2=k2+data(i,:);
         n2=n2+1;
         plot(data(i,1),data(i,2),'b.');
         end
         end
         m1=k1/n1;
         m2=k2/n2;
        % plot(m1(1,1),m1(1,2),'g.');
        % plot(m2(1,1),m2(1,2),'g.');
         k1=zeros(1,2);
         k2=zeros(1,2);
         n1=0;
         n2=0;
        end
        plot(m1(1,1),m1(1,2),'k*');
        plot(m2(1,1),m2(1,2),'k*');
        title('k-means聚类');
        hold off;
    
   

输出结果（未分类数据是由已分类数据去掉标签，黑色※号表示聚类中心）：

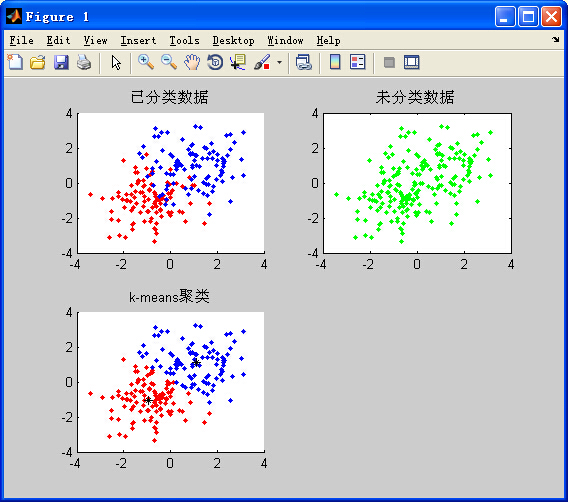
二、高斯混合模型（GMM）

           回想之前之前的高斯判别分析法（GDA），是通过计算样本的后验概率来进行判别，而后验概率是通过假设多元高斯模型来计算得来的。高斯模型的参数：均值、协方差，是由已标定（分类）的样本得来，所以可以看做是一种监督学习方法。

        在GMM模型（属于无监督学习），给定未分类的m个样本（n维特征），假设可分为k个类，要求用GMM算法对其进行分类。如果我们知道每个类的高斯参数，则可以向GDA算法那样计算出后验概率进行判别。但遗憾的是，杨输入的样本未被标定，也就是说我们得不到高斯参数：均值、协方差。这就引出EM（Expectation Maximization Algorithm：期望最大化）算法。

        EM算法的思想有点类似于k-means，就是通过迭代来得出最好的参数，有了这些参数就可以像GDA那样做分类了。GMM及EM具体步骤如下：

MATLAB代码如下：

[cpp] view plain copy

print ?

1. %%  
2. %GMM算法（高斯混合模型）soft assignment（软划分）  
3. clear all;  
4. close all;  
5. %%  
6. k=2;%聚类数  
7. n=2;%维数  
8. m=200;  
9. % v0=randn(m/2,2)-1;  
10. % v1=randn(m/2,2)+1;  
11. v0=mvnrnd([1 1],[1 0;0 1],m/2);%生成正样本1  
12. v1=mvnrnd([4 4],[1 0;0 1],m/2);%生成负样本0  
13. figure;subplot(221);  
14. hold on;  
15. plot(v0(:,1),v0(:,2),'r.');  
16. plot(v1(:,1),v1(:,2),'b.');  
17. title('已分类数据');  
18. hold off;  
19. %%  
20. data=[v0;v1];  
21. data=sortrows(data,1);  
22. subplot(222);  
23. plot(data(:,1),data(:,2),'g.');  
24. title('未分类数据');  
25. %%  
26. mu1=mean(data(1:50,:));  
27. mu2=mean(data(100:180,:));  
28. sigma1=cov(data(1:50,:));  
29. sigma2=cov(data(100:180,:));  
30. p=zeros(m,k);%概率  
31. thresh=0.05;%迭代终止条件  
32. iter=0;%记录迭代次数  
33. while(1)  
34.     iter=iter+1;  
35.     A1=1/(((2*pi)^(n/2))*((det(sigma1))^(1/2)));  
36.     A2=1/(((2*pi)^(n/2))*((det(sigma2))^(1/2)));  
37.     for i=1:m  
38.         p(i,1)=A1*exp((-1/2)*(data(i,:)-mu1)*sigma1*(data(i,:)-mu1)');  
39.         p(i,2)=A2*exp((-1/2)*(data(i,:)-mu2)*sigma2*(data(i,:)-mu2)');  
40.         pp=sum(p(i,:));  
41.         p(i,1)=p(i,1)/pp;%归一化，样本属于某类的概率的总和为1  
42.         p(i,2)=p(i,2)/pp;  
43.     end  
44.     sum1=zeros(n,n);  
45.     sum2=zeros(n,n);  
46.     for i=1:m  
47.         sum1=sum1+p(i,1)*(data(i,:)-mu1)'*(data(i,:)-mu1);  
48.         sum2=sum2+p(i,2)*(data(i,:)-mu2)'*(data(i,:)-mu2);  
49.     end  
50.     sigma1=sum1/sum(p(:,1));  
51.     sigma2=sum2/sum(p(:,2));  
52.     mu1_pre=mu1;  
53.     mu2_pre=mu2;  
54.     mu1=(p(:,1)'*data)/sum(p(:,1));  
55.     mu2=(p(:,2)'*data)/sum(p(:,2));  
56.     if ((pdist2(mu1_pre,mu1)<=thresh) || (pdist2(mu2_pre,mu2)<=thresh))  
57.         break;  
58.     end  
59. end  
60. %%  
61. subplot(223);  
62. hold on;  
63. A1=1/(((2*pi)^(n/2))*((det(sigma1))^(1/2)));  
64. A2=1/(((2*pi)^(n/2))*((det(sigma2))^(1/2)));  
65. for i=1:m  
66.     p(i,1)=A1*exp((-1/2)*(data(i,:)-mu1)*sigma1*(data(i,:)-mu1)');  
67.     p(i,2)=A2*exp((-1/2)*(data(i,:)-mu2)*sigma2*(data(i,:)-mu2)');  
68.     if p(i,1)>=p(i,2)  
69.         plot(data(i,1),data(i,2),'r.');  
70.     else  
71.         plot(data(i,1),data(i,2),'b.');  
72.     end  
73. end  
74. title('GMM分类');  
75. hold off;  
76. %完  

        %%
        %GMM算法（高斯混合模型）soft assignment（软划分）
        clear all;
        close all;
        %%
        k=2;%聚类数
        n=2;%维数
        m=200;
        % v0=randn(m/2,2)-1;
        % v1=randn(m/2,2)+1;
        v0=mvnrnd([1 1],[1 0;0 1],m/2);%生成正样本1
        v1=mvnrnd([4 4],[1 0;0 1],m/2);%生成负样本0
        figure;subplot(221);
        hold on;
        plot(v0(:,1),v0(:,2),'r.');
        plot(v1(:,1),v1(:,2),'b.');
        title('已分类数据');
        hold off;
        %%
        data=[v0;v1];
        data=sortrows(data,1);
        subplot(222);
        plot(data(:,1),data(:,2),'g.');
        title('未分类数据');
        %%
        mu1=mean(data(1:50,:));
        mu2=mean(data(100:180,:));
        sigma1=cov(data(1:50,:));
        sigma2=cov(data(100:180,:));
        p=zeros(m,k);%概率
        thresh=0.05;%迭代终止条件
        iter=0;%记录迭代次数
        while(1)
         iter=iter+1;
         A1=1/(((2*pi)^(n/2))*((det(sigma1))^(1/2)));
         A2=1/(((2*pi)^(n/2))*((det(sigma2))^(1/2)));
        for i=1:m
         p(i,1)=A1*exp((-1/2)*(data(i,:)-mu1)*sigma1*(data(i,:)-mu1)');
         p(i,2)=A2*exp((-1/2)*(data(i,:)-mu2)*sigma2*(data(i,:)-mu2)');
         pp=sum(p(i,:));
         p(i,1)=p(i,1)/pp;%归一化，样本属于某类的概率的总和为1
         p(i,2)=p(i,2)/pp;
         end
         sum1=zeros(n,n);
         sum2=zeros(n,n);
        for i=1:m
         sum1=sum1+p(i,1)*(data(i,:)-mu1)'*(data(i,:)-mu1);
         sum2=sum2+p(i,2)*(data(i,:)-mu2)'*(data(i,:)-mu2);
         end
         sigma1=sum1/sum(p(:,1));
         sigma2=sum2/sum(p(:,2));
         mu1_pre=mu1;
         mu2_pre=mu2;
         mu1=(p(:,1)'*data)/sum(p(:,1));
         mu2=(p(:,2)'*data)/sum(p(:,2));
        if ((pdist2(mu1_pre,mu1)<=thresh) || (pdist2(mu2_pre,mu2)<=thresh))
        break;
         end
        end
        %%
        subplot(223);
        hold on;
        A1=1/(((2*pi)^(n/2))*((det(sigma1))^(1/2)));
        A2=1/(((2*pi)^(n/2))*((det(sigma2))^(1/2)));
        for i=1:m
         p(i,1)=A1*exp((-1/2)*(data(i,:)-mu1)*sigma1*(data(i,:)-mu1)');
         p(i,2)=A2*exp((-1/2)*(data(i,:)-mu2)*sigma2*(data(i,:)-mu2)');
        if p(i,1)>=p(i,2)
         plot(data(i,1),data(i,2),'r.');
        else
         plot(data(i,1),data(i,2),'b.');
        end
        end
        title('GMM分类');
        hold off;
        %完
    
   

输出结果：

文章来源: blog.csdn.net，作者：网奇，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/jacke121/article/details/78488987