机器学习系列之EM算法
机器学习系列之EM算法
我讲EM算法的大概流程主要三部分：需要的预备知识、EM算法详解和对EM算法的改进。
一、EM算法的预备知识
1、极大似然估计
（1）举例说明：经典问题——学生身高问题
我们需要调查我们学校的男生和女生的身高分布。 假设你在校园里随便找了100个男生和100个女生。他们共200个人。将他们按照性别划分为两组，然后先统计抽样得到的100个男生的身高。假设他们的身高是服从高斯分布的。但是这个分布的均值u和方差∂2我们不知道，这两个参数就是我们要估计的。记作θ=[u, ∂]T。
问题：我们知道样本所服从的概率分布的模型和一些样本，而不知道该模型中的参数。
我们已知的有两个：（1）样本服从的分布模型（2）随机抽取的样本 需要通过极大似然估计求出的包括：模型的参数
总的来说：极大似然估计就是用来估计模型参数的统计学方法。
（2）如何估计
问题数学化： （1）样本集X={x1,x2,…,xN} N=100 （2）概率密度：p(xi|θ)抽到男生i（的身高）的概率 100个样本之间独立同分布，所以我同时抽到这100个男生的概率就是他们各自概率的乘积。就是从分布是p(x|θ)的总体样本中抽取到这100个样本的概率，也就是样本集X中各个样本的联合概率，用下式表示：
这个概率反映了，在概率密度函数的参数是θ时，得到X这组样本的概率。 需要找到一个参数θ，其对应的似然函数L(θ)最大，也就是说抽到这100个男生（的身高）概率最大。这个叫做θ的最大似然估计量，记为
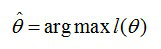
（3）求最大似然函数估计值的一般步骤
首先，写出似然函数：
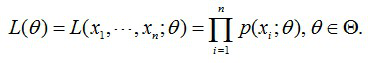
其次，对似然函数取对数，并整理：
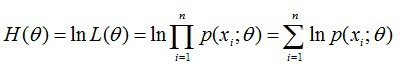
然后，求导数，令导数为0，得到似然方程；
最后，解似然方程，得到的参数即为所求。
（4）总结
多数情况下我们是根据已知条件来推算结果，而极大似然估计是已经知道了结果，然后寻求使该结果出现的可能性最大的条件，以此作为估计值。
2、Jensen不等式
（1）定义
设f是定义域为实数的函数，如果对于所有的实数x。如果对于所有的实数x，f(x)的二次导数大于等于0，那么f是凸函数。 Jensen不等式表述如下： 如果f是凸函数，X是随机变量，那么：E[f(X)]>=f(E[X]) 。当且仅当X是常量时，上式取等号。
（2）举例
图中，实线f是凸函数，X是随机变量，有0.5的概率是a，有0.5的概率是b。X的期望值就是a和b的中值了，图中可以看到E[f(X)]>=f(E[X])成立。 Jensen不等式应用于凹函数时，不等号方向反向。
二、传统EM算法详述
1、问题描述
我们抽取的100个男生和100个女生样本的身高，但是我们不知道抽取的那200个人里面的每一个人到底是从男生的那个身高分布里面抽取的，还是女生的那个身高分布抽取的。 用数学的语言就是，抽取得到的每个样本都不知道是从哪个分布抽取的。 这个时候，对于每一个样本，就有两个东西需要猜测或者估计： （1）这个人是男的还是女的？（2）男生和女生对应的身高的高斯分布的参数是多少？
EM算法要解决的问题是： （1）求出每一个样本属于哪个分布 （2）求出每一个分布对应的参数
2、举例说明
身高问题使用EM算法求解步骤：
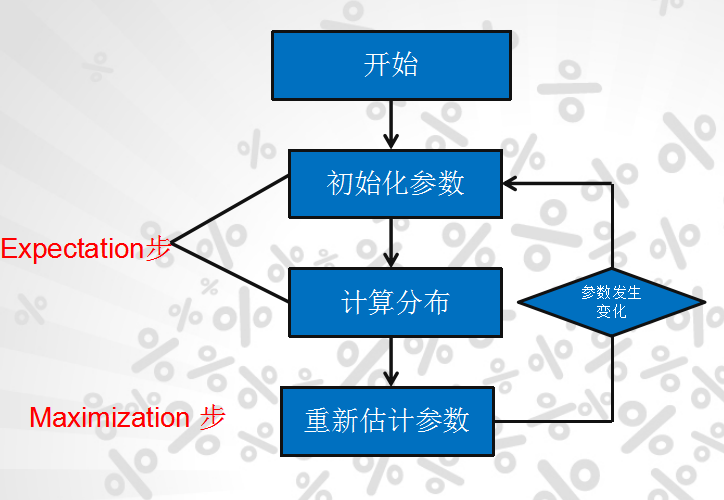
（1）初始化参数：先初始化男生身高的正态分布的参数：如均值=1.7，方差=0.1
（2）计算每一个人更可能属于男生分布或者女生分布；
（3）通过分为男生的n个人来重新估计男生身高分布的参数（最大似然估计），女生分布也按照相同的方式估计出来，更新分布。
（4）这时候两个分布的概率也变了，然后重复步骤（1）至（3），直到参数不发生变化为止。
3、算法推导
已知：样本集X={x(1),…,x(m))}，包含m个独立的样本；
未知：每个样本i对应的类别z(i)是未知的（相当于聚类）；
输出：我们需要估计概率模型p(x,z)的参数θ；
目标：找到适合的θ和z让L(θ)最大。
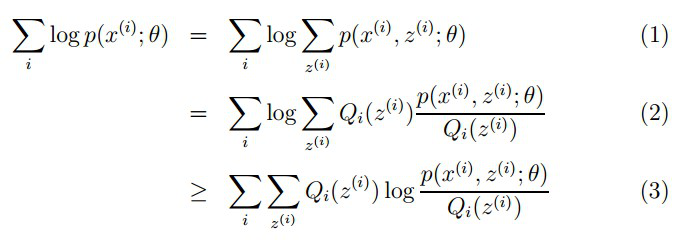
要使L(θ)最大，我们可以不断最大化下界J，来使得L(θ)不断提高，达到最大值。
问题：
什么时候下界J(z,Q)与L(θ)在此点θ处相等？
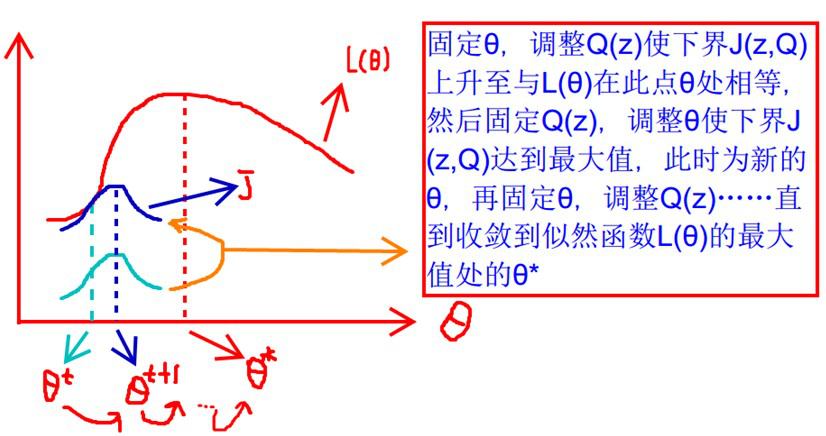
根据Jensen不等式，自变量X是常数，等式成立。即：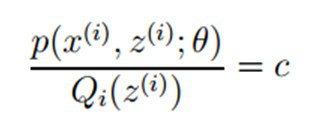
由于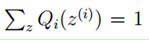
，则可以得到：分子的和等于c
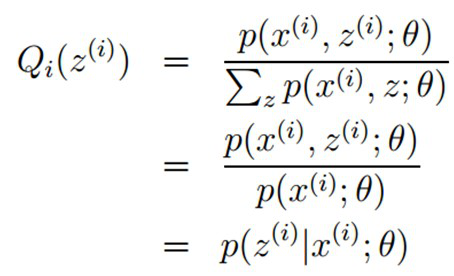
在固定参数θ后，使下界拉升的Q(z)的计算公式，解决了Q(z)如何选择的问题。这一步就是E步，建立L(θ)的下界。接下来的M步，就是在给定Q(z)后，调整θ，去极大化L(θ)的下界J。
4、算法流程
1）初始化分布参数θ； 重复以下步骤直到收敛：
E步骤：根据参数初始值或上一次迭代的模型参数来计算出隐性变量的后验概率，其实就是隐性变量的期望。作为隐藏变量的现估计值：
M步骤：将似然函数最大化以获得新的参数值：
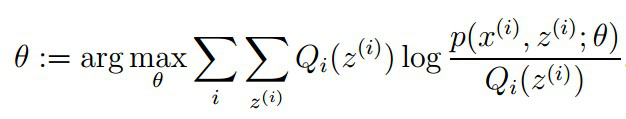
5、总结
期望最大算法（EM算法）是一种从不完全数据或有数据丢失的数据集（存在隐含变量）中求解概率模型参数的最大似然估计方法。
三、EM算法的初始化研究
1、问题描述
EM算法缺陷之一：传统的EM算法对初始值敏感，聚类结果随不同的初始值而波动较大。总的来说，EM算法收敛的优劣很大程度上取决于其初始参数。
我看了一篇论文：地址：https://yunpan.cn/cqmW9vurLFmDT 访问密码 0e74
本篇论文采用的方法：采用一种基于网格的聚类算法来初始化EM算法。
2、基本思想
基于网格的聚类算法将数据空间的每一维平均分割成等长的区间段, 从而将数据空间分成不相交的网格单元。由于同个网格单元中的点属于同一类的可能性比较大, 所以落入同一网格单元中的点可被看作一个对象进行处理, 以后所有的聚类操作都在网格单元上进行。 因此，基于网格的聚类过程只与网格单元的个数有关, 聚类的效率得到了很大的提高。
3、算法步骤
（1）定义：
（2）相似度：数据对象间的相似性是基于对象间的距离来计算的。
（3）输入输出：
（4）算法步骤
4、总结
我觉得这篇论文的主要思想应该是这样的：就拿身高举例。它就是首先做一个预处理，将身高在一个范围内（例如1.71至1.74）的分成一个网格，再看这个网格占全部数据的多少，以此判断出该网格为高密度还是低密度，然后循环算出所有网格的，再使用EM算法计算哪些高密度网格，这样会使整个算法收敛的快一些。还有一些其他的论文也是讲的这个。
EM算法一般表述：
当有部分数据缺失或者无法观察到时，EM算法提供了一个高效的迭代程序用来计算这些数据的最大似然估计。在每一步迭代分为两个步骤：期望（Expectation）步骤和最大化（Maximization）步骤，因此称为EM算法。
假设全部数据Z是由可观测到的样本X={X1, X2，……, Xn}和不可观测到的样本Z={Z1, Z2，……, Zn}组成的，则Y = X∪Z。EM算法通过搜寻使全部数据的似然函数Log(L(Z; h))的期望值最大来寻找极大似然估计，注意此处的h不是一个变量，而是多个变量组成的参数集合。此期望值是在Z所遵循的概率分布上计算，此分布由未知参数h确定。然而Z所遵循的分布是未知的。EM算法使用其当前的假设h`代替实际参数h，例如：给出假设均值u等，以估计Z的分布。
Q( h`| h) = E [ ln P(Y|h`) | h, X ]
EM算法重复以下两个步骤直至收敛。
步骤1：估计（E）步骤：使用当前假设h和观察到的数据X来估计Y上的概率分布以计算Q( h` | h )。
Q( h` | h ) ←E[ ln P(Y|h`) | h, X ]
步骤2：最大化（M）步骤：将假设h替换为使Q函数最大化的假设h`:
h ←argmaxQ( h` | h )
高斯混合模型参数估计问题：
Python实现（模拟2个正态分布的均值估计）：
#coding:gbk
import math
import copy
import numpy as np
import matplotlib.pyplot as plt
isdebug = False
# 指定k个高斯分布参数，这里指定k=2。注意2个高斯分布具有相同均方差Sigma，分别为Mu1,Mu2。
def ini_data(Sigma,Mu1,Mu2,k,N):
global X #X产生的数据 ,k维向量
global Mu #初始均值
global Expectations
X = np.zeros((1,N))
Mu = np.random.random(2) #随机产生一个初始均值。
Expectations = np.zeros((N,k)) #k个高斯分布，100个二维向量组成的矩阵。
for i in range(0,N):
if np.random.random(1) > 0.5:
#随机从均值为Mu1,Mu2的分布中取样。
X[0,i] = np.random.normal()*Sigma + Mu1
else:
X[0,i] = np.random.normal()*Sigma + Mu2
if isdebug:
print("***********")
print(u"初始观测数据X：")
print(X)
# EM算法：步骤1，计算E[zij]
def e_step(Sigma,k,N):
#求期望。sigma协方差，k高斯混合模型数，N数据个数。
global Expectations #N个k维向量
global Mu
global X
for i in range(0,N):
Denom = 0
for j in range(0,k):
Denom += math.exp((-1/(2*(float(Sigma**2))))*(float(X[0,i]-Mu[j]))**2)
#Denom 分母项 Mu(j)第j个高斯分布的均值。
for j in range(0,k):
Numer = math.exp((-1/(2*(float(Sigma**2))))*(float(X[0,i]-Mu[j]))**2) #分子项
Expectations[i,j] = Numer / Denom #期望，计算出每一个高斯分布所占的期望，即该高斯分布以多大比例形成这个样本
#if isdebug:
#print("***********")
#print(u"隐藏变量E（Z）：")
#print(Expectations)
# EM算法：步骤2，求最大化E[zij]的参数Mu
def m_step(k,N):
#最大化
global Expectations #期望值
global X #数据
for j in range(0,k):
#遍历k个高斯混合模型数据
Numer = 0 #分子项
Denom = 0 #分母项
for i in range(0,N):
Numer += Expectations[i,j]*X[0,i] # 每一个高斯分布的期望*该样本的值。
Denom += Expectations[i,j] #第j个高斯分布的总期望值作为分母
Mu[j] = Numer / Denom #第j个高斯分布新的均值，
# 算法迭代iter_num次，或达到精度Epsilon停止迭代
def run(Sigma,Mu1,Mu2,k,N,iter_num,Epsilon):
ini_data(Sigma,Mu1,Mu2,k,N)
print(X)
print(u"初始<u1,u2>:", Mu) #初始均值
for i in range(iter_num):
Old_Mu = copy.deepcopy(Mu) #算法之前的MU
e_step(Sigma,k,N)
m_step(k,N)
print(i,Mu) #经过EM算法之后的MU，
if sum(abs(Mu-Old_Mu)) < Epsilon:
break
if __name__ == '__main__':
run(6,40,20,2,100,100,0.001)
plt.hist(X[0,:],50)
plt.show()
本代码用于模拟k=2个正态分布的均值估计。其中ini_data(Sigma,Mu1,Mu2,k,N)函数用于生成训练样本，此训练样本时从两个高斯分布中随机生成的，其中高斯分布a均值Mu1=40、均方差Sigma=6，高斯分布b均值Mu2=20、均方差Sigma=6，生成的样本分布如下图所示。由于本问题中实现无法直接冲样本数据中获知两个高斯分布参数，因此需要使用EM算法估算出具体Mu1、Mu2取值。
图 1 样本数据分布
在图1的样本数据下，在第11步时，迭代终止，EM估计结果为：
Mu=[ 40.55261688 19.34252468]
文章来源: blog.csdn.net，作者：网奇，版权归原作者所有，如需转载，请联系作者。
原文链接：blog.csdn.net/jacke121/article/details/78489447
- 点赞
- 收藏
- 关注作者
评论（0）