聚类常见距离及python实现

主要内容
层次聚类类型：硬聚类、软聚类；聚合聚类、分裂聚类定义理解
欧氏与闵氏距离的缺陷分析：欧氏距离、闵可夫斯基距离的适用范围
兰氏距离：表达式与数学性质，距离适用范围
马氏距离：表达式与数学性质，距离适用范围
斜交空间距离：表达式与数学性质，距离适用范围
相似系数的算法：两个n维变量间的相似测度，计算公式
夹角余弦：几类特殊的夹角余弦的表达式与区别

层次聚类
层次聚类假设类别之间存在层次结构，将样本聚到层次化的类中。
层次聚类⼜有聚合（agglomerative）或⾃下⽽上（bottom-up）聚类、分裂（divisive）或⾃上⽽下（top-down）聚类两种⽅法。
因为每个样本只属于⼀个类，所以层次聚类属于硬聚类。
1.聚合聚类
开始将每个样本各⾃分到⼀个类,之后将相距最近的两类合并，建⽴⼀个新的类，重复此操作直到满⾜停⽌条件，得到层次化的类别
2.分裂聚类
开始将所有样本分到⼀个类,之后将已有类中相距最远的样本分到两个新的类，重复此操作直到满⾜停⽌条件，得到层次化的类别

这里的停止条件可以是类别数量达到阈值或者类间距达到阈值。

欧式距离的缺陷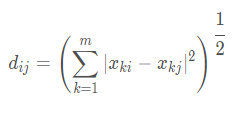

受量纲的影响明显：不同单位之间不能计算欧式距离；
未考虑个变量⽅差的不同，如果某个特征分布差异较大，效果也不好，可以用归

文章来源: blog.csdn.net，作者：网奇，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/jacke121/article/details/115874518