k-means——平面上100个样本点的聚类分析(通俗易懂)
【摘要】 1、k-means聚类的算法流程
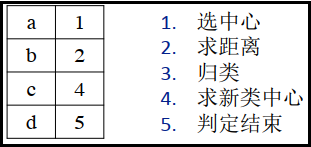
1.随机选取n个样本作为初始类中心;2.计算各样本与各类中心的距离;3.将各样本归于最近的类中心点;4.求各类的样本的均值,作为新的类中心;5.判定:若类中心不再发生变动或达到指定迭代次数,那么算法结束,否则回到第2步。
2、一个形象的例子:讲述k-means聚类原理
1)将下面这四个点,分为两类
2)聚类流程如下
...
1、k-means聚类的算法流程
- 1.随机选取n个样本作为初始类中心;
- 2.计算各样本与各类中心的距离;
- 3.将各样本归于最近的类中心点;
- 4.求各类的样本的均值,作为新的类中心;
- 5.判定:若类中心不再发生变动或达到指定迭代次数,那么算法结束,否则回到第2步。

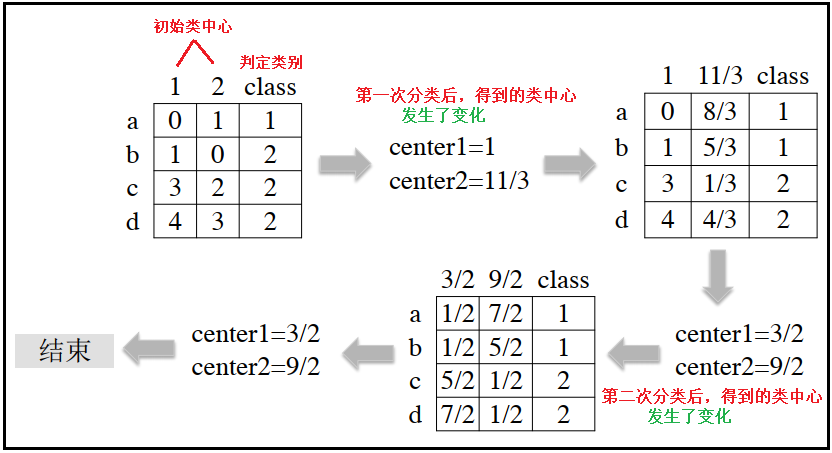
2、一个形象的例子:讲述k-means聚类原理
1)将下面这四个点,分为两类
2)聚类流程如下
3、平面上100个点的k-means聚类分析
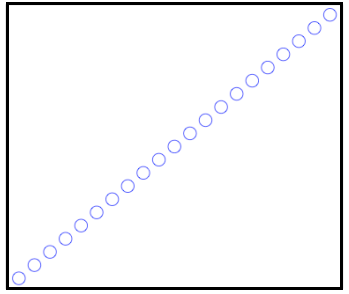
代码如下:
import numpy as np
# 构造数据集
x = np.linspace(0,99,100)
y = np.linspace(100,199,100)
aa = 0 # aa变量是为了记录,迭代次数
k = 2 # 指定将数据分为几个类别
n = len(x) # 数据集的个数
# 1、随机选取两个点,作为初始的类中心;
center0 = np.array([x[0],y[0]])
center1 = np.array([x[1],y[1]])
dis = np.zeros([n,k+1])
while aa >= 0: # 2、求各样本到各类中心的距离; for i in range(n): dis[i,0] = np.sqrt((x[i]-center0[0])**2+(y[i]-center0[1])**2) dis[i,1] = np.sqrt((x[i]-center1[0])**2+(y[i]-center1[1])**2) # 3、归类:将样本归类为,距离其最近的类中的所属类; dis[i,2] = np.argmin(dis[i,:2]) # 4、再次计算各类样本的均值,作为新的类中心; index0 = dis[:,2] == 0 index1 = dis[:,2] == 1 center0_new = np.array([x[index0].mean(),y[index0].mean()]) center1_new = np.array([x[index1].mean(),y[index1].mean()]) # 5、判断类中心,是否发生变化。如果发生变化,就回到第2步;否则,break退出循环; if all((center0 == center0_new) & (center1 == center1_new)): break center0 = center0_new center1 = center1_new aa += 1
print(len(dis[dis[:,2] == 0]),len(dis[dis[:,2] == 1]))
print(center0,center1,aa)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
结果如下:

结果分析:
从上面的结果中可以看到,最终的数据被分为的两类,每一类各有50个点。同时我们求出了最终的类中心点,一个是(24,5,124,5),另一个是(74.5,174.5),并且还求出了最后的迭代次数为7,也就是说:初始类中心一共迭代了7次后,就不再发生变化了。
文章来源: blog.csdn.net,作者:数据分析与统计学之美,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/weixin_41261833/article/details/104513778
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)