Python建立时间序列ARIMA模型实战案例
> 本文将介绍使用Python来完成时间序列分析ARIMA模型的完整步骤与流程,绘制时序图,平稳性检验,单位根检验,白噪声检验,模型定阶,模型有啊,参数估计,模型检验等完整步骤。

时间序列分析概念

时间序列分析 是统计学中的一个非常重要的分支,是以概率论与数理统计为基础、计算机应用为技术支撑,迅速发展起来的一种应用性很强的科学方法。时间序列是变量按时间间隔的顺序而下形成的随机变量序列,大量自然界、社会经济等领域的统计指标都依年、季、月或日统计其指标值,随着时间的推移,形成了统计指标的时间序列,例如,股价指数、物价指数、GDP和产品销售量等等都属于时间序列。
建立模型基本步骤
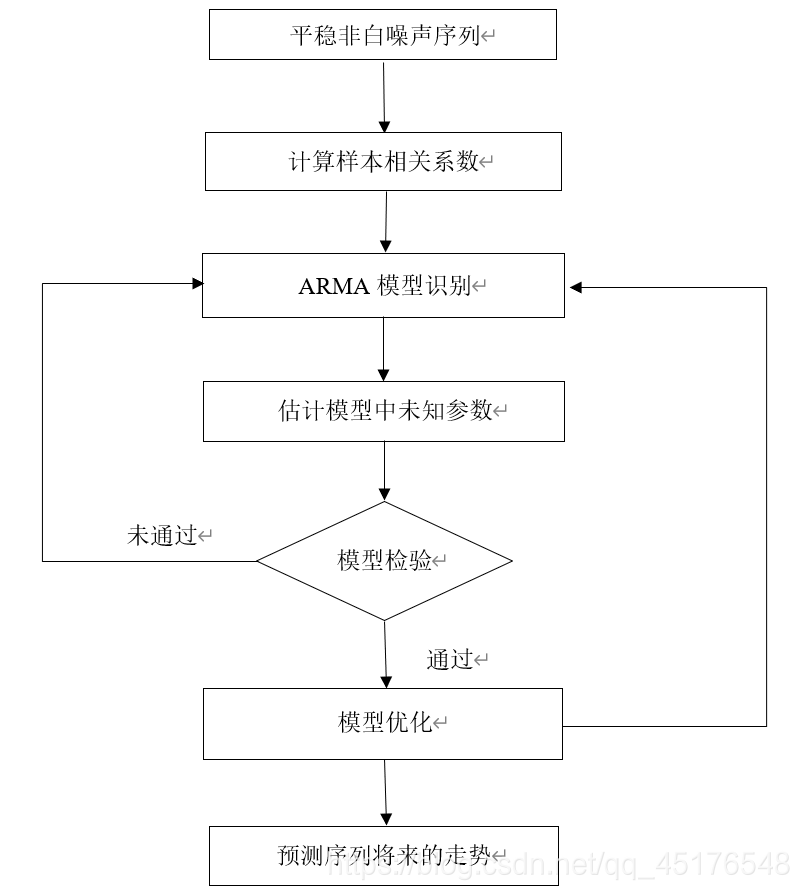
ARIMA模型建模实战
导入模块
import sys
import os
import pandas as pd
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
from statsmodels.tsa.stattools import adfuller
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.graphics.api import qqplot
import matplotlib.pylab as plt
from matplotlib.pylab import style
style.use('ggplot')
from arch.unitroot import ADF
import warnings
warnings.filterwarnings("ignore")
pd.set_option('display.float_format', lambda x: '%.5f' % x)
np.set_printoptions(precision=5, suppress=True)
pd.set_option('display.max_columns', 100)
pd.set_option('display.max_rows', 100)
%matplotlib inline
"""中文显示问题"""
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
加载数据
data = pd.read_excel("data.xlsx",index_col="年份",parse_dates=True)
data.head()
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| xt | |
|---|---|
| 年份 | |
| 1952-01-01 | 100.00000 |
| 1953-01-01 | 101.60000 |
| 1954-01-01 | 103.30000 |
| 1955-01-01 | 111.50000 |
| 1956-01-01 | 116.50000 |
平稳性检验
时序图
data["diff1"] = data["xt"].diff(1).dropna()
data["diff2"] = data["diff1"].diff(1).dropna()
data1 = data.loc[:,["xt","diff1","diff2"]]
data1.plot(subplots=True, figsize=(18, 12),title="差分图")

时序图检验 - - 全靠肉眼的判断和判断人的经验,不同的人看到同样的图形,很可能会给出不同的判断。因此我们需要一个更有说服力、更加客观的统计方法来帮助我们检验时间序列的平稳性,这种方法,就是单位根检验。
原文链接:https://blog.csdn.net/qq_45176548/article/details/111504846
单位根检验
print("单位根检验:\n")
print(ADF(data.diff1.dropna()))
单位根检验:
Augmented Dickey-Fuller Results
=====================================
Test Statistic -3.156
P-value 0.023
Lags 0
-------------------------------------
Trend: Constant
Critical Values: -3.63 (1%), -2.95 (5%), -2.61 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.
**单位根检验** - -对其一阶差分进行单位根检验,得到:1%、%5、%10不同程度拒绝原假设的统计值和ADF Test result的比较,本数据中,P-value 为 0.023,接近0,ADF Test result同时小于5%、10%即说明很好地拒绝该假设,本数据中,ADF结果为-3.156,拒绝原假设,即一阶差分后数据是平稳的。
白噪声检验
判断序列是否为非白噪声序列
from statsmodels.stats.diagnostic import acorr_ljungbox
acorr_ljungbox(data.diff1.dropna(), lags = [i for i in range(1,12)],boxpierce=True)
(array([11.30402, 13.03896, 13.37637, 14.24184, 14.6937 , 15.33042,
16.36099, 16.76433, 18.15565, 18.16275, 18.21663]),
array([0.00077, 0.00147, 0.00389, 0.00656, 0.01175, 0.01784, 0.02202,
0.03266, 0.03341, 0.05228, 0.07669]),
array([10.4116 , 11.96391, 12.25693, 12.98574, 13.35437, 13.85704,
14.64353, 14.94072, 15.92929, 15.93415, 15.9696 ]),
array([0.00125, 0.00252, 0.00655, 0.01135, 0.02027, 0.03127, 0.04085,
0.06031, 0.06837, 0.10153, 0.14226]))
通过P<α,拒绝原假设,故差分后的序列是平稳的非白噪声序列,可以进行下一步建模
模型定阶
现在我们已经得到一个平稳的时间序列,接来下就是选择合适的ARIMA模型,即ARIMA模型中合适的p,q。
第一步我们要先检查平稳时间序列的自相关图和偏自相关图。通过sm.graphics.tsa.plot_acf和sm.graphics.tsa.plot_pacf得到图形
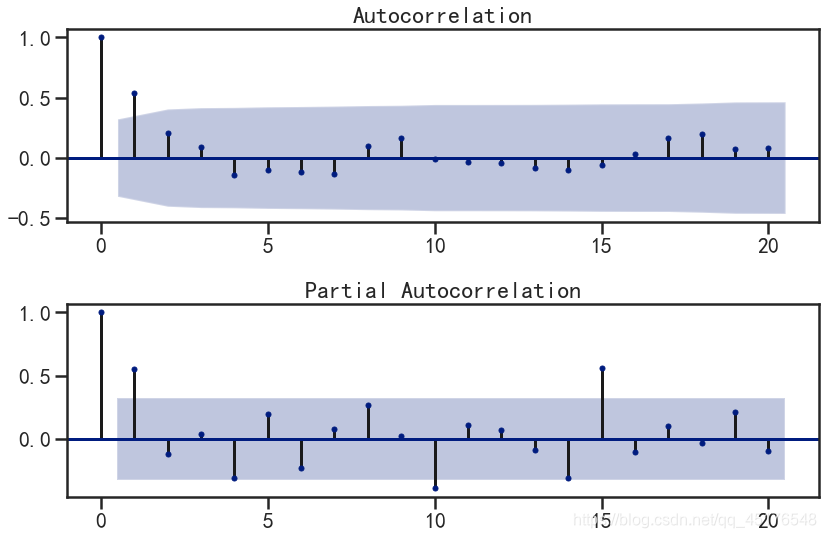
从一阶差分序列的自相关图和偏自相关图可以发现:
- 自相关图拖尾或一阶截尾
- 偏自相关图一阶截尾,
- 所以我们可以建立ARIMA(1,1,0)、ARIMA(1,1,1)、ARIMA(0,1,1)模型。
模型优化

- 其中L是在该模型下的最大似然,n是数据数量,k是模型的变量个数。
python代码如下:
arma_mod20 = sm.tsa.ARIMA(data["xt"],(1,1,0)).fit()
arma_mod30 = sm.tsa.ARIMA(data["xt"],(0,1,1)).fit()
arma_mod40 = sm.tsa.ARIMA(data["xt"],(1,1,1)).fit()
values = [[arma_mod20.aic,arma_mod20.bic,arma_mod20.hqic],[arma_mod30.aic,arma_mod30.bic,arma_mod30.hqic],[arma_mod40.aic,arma_mod40.bic,arma_mod40.hqic]]
df = pd.DataFrame(values,index=["AR(1,1,0)","MA(0,1,1)","ARMA(1,1,1)"],columns=["AIC","BIC","hqic"])
df
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| AIC | BIC | hqic | |
|---|---|---|---|
| AR(1,1,0) | 253.09159 | 257.84215 | 254.74966 |
| MA(0,1,1) | 251.97340 | 256.72396 | 253.63147 |
| ARMA(1,1,1) | 254.09159 | 258.84535 | 259.74966 |
- 构造这些统计量所遵循的统计思想是一致的,就是在考虑拟合残差的同时,依自变量个数施加“惩罚”。但要注意的是,这些准则不能说明某一个模型的精确度,也即是说,对于三个模型A,B,C,我们能够判断出B模型是最好的,但不能保证B模型能够很好地刻画数据
参数估计
from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(data["xt"], order=(0,1,1))
result = model.fit()
print(result.summary())
ARIMA Model Results
==============================================================================
Dep. Variable: D.xt No. Observations: 36
Model: ARIMA(0, 1, 1) Log Likelihood -122.987
Method: css-mle S.D. of innovations 7.309
Date: Tue, 22 Dec 2020 AIC 251.973
Time: 09:11:55 BIC 256.724
Sample: 01-01-1953 HQIC 253.631
- 01-01-1988
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 4.9956 2.014 2.481 0.013 1.048 8.943
ma.L1.D.xt 0.6710 0.165 4.071 0.000 0.348 0.994
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
MA.1 -1.4902 +0.0000j 1.4902 0.5000
-----------------------------------------------------------------------------
模型检验

参数的显著性检验


P<α,拒绝原假设,认为该参数显著非零MA(2)模型拟合该序列,残差序列已实现白噪声
模型的显著性检验

resid = result.resid#残差
fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(111)
fig = qqplot(resid, line='q', ax=ax, fit=True)

qq图显示,我们看到红色的KDE线与N(0,1)平行,这是残留物正太分布的良好指标,说明残差序列是白噪声序列,模型的信息的提取充分,当让大家也可以使用前面介绍的检验白噪声的方法LB统计量来检验
ARIMA(0,1,1)模型拟合该序列,残差序列已实现白噪声,且参数均显著非零。说明AR(0,11)模型是该序列的有效拟合模型
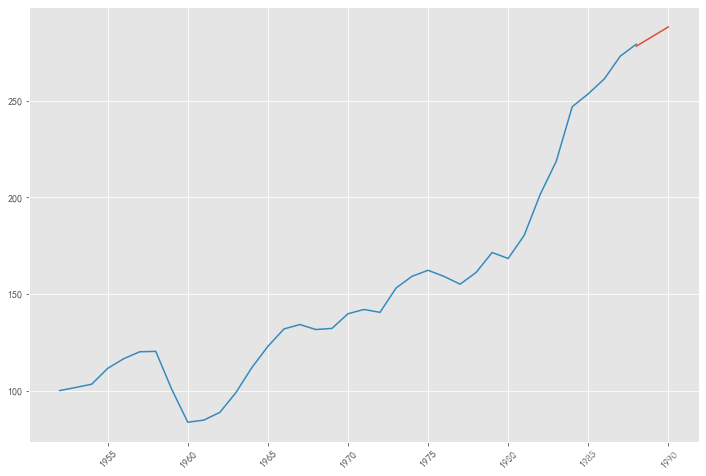
模型预测
pred = result.predict('1988', '1990',dynamic=True, typ='levels')
print (pred)
1988-01-01 278.35527
1989-01-01 283.35088
1990-01-01 288.34649
Freq: AS-JAN, dtype: float64
plt.figure(figsize=(12, 8))
plt.xticks(rotation=45)
plt.plot(pred)
plt.plot(data.xt)
plt.show()
推荐阅读
- 冰冰B站视频弹幕爬取原理解析
- 使用xpath爬取数据
- jupyter notebook使用
- BeautifulSoup爬取豆瓣电影Top250
- 一篇文章带你掌握requests模块
- Python网络爬虫基础–BeautifulSoup
到这里就结束了,如果对你有帮助你,欢迎点赞关注,你的点赞对我很重要
- 点赞
- 收藏
- 关注作者



评论(0)