Python OpenCV 之图像金字塔,高斯金字塔与拉普拉斯金字塔
Python OpenCV 365 天学习计划,与橡皮擦一起进入图像领域吧。
基础知识铺垫
学习图像金字塔,发现网上的资料比较多,检索起来比较轻松。
图像金字塔是一张图像多尺度的表达,或者可以理解成一张图像不同分辨率展示。
金字塔越底层的图片,像素越高,越向上,像素逐步降低,分辨率逐步降低。
高斯金字塔
我们依旧不对概念做过多解释,第一遍学习应用,应用,毕竟 365 天的周期,时间长,后面补充理论知识。
高斯金字塔用于向下采样,同时它也是最基本的图像塔。
在互联网检索原理,得到最简单的说明如下:
将图像的最底层(高斯金字塔的第 0 层),例如高斯核(5x5)对其进行卷积操作,这里的卷积主要处理掉的是偶数行与列,然后得到金字塔上一层图像(即高斯金字塔第 1 层),在针对该图像重复卷积操作,得到第 2 层,反复执行下去,即可得到高斯金字塔。
每次操作之后,都会将 M×N 图像变成 M/2 × N/2 图像,即减少一半。
还有实测中发现,需要用图像的宽和高一致的图片,并且宽高要是 2 的次幂数,例如,8 像素,16 像素,32 像素等等,一会你也可以实际测试一下。
图像金字塔应用到的函数有 cv2.pyrDown() 和 cv2.pyrUp() 。
cv2.pyrDown 与 cv2.pyrUp 函数原型
通过 help 函数得到函数原型如下:
pyrDown(src[, dst[, dstsize[, borderType]]]) -> dst
pyrUp(src[, dst[, dstsize[, borderType]]]) -> dst
- 1
- 2
两个函数原型参数一致,参数说明如下:
- src:输入图像;
- dst: 输出图像;
- dstsize: 输出图像尺寸,默认值按照
((src.cols+1)/2, (src.rows+1)/2)计算。
关于两个函数的补充说明:
- cv2.pyrDown 从一个相对高分辨率的大尺寸的图像上构建一个金字塔,运行之后的结果是,图像变小,分辨率降低(下采样);
- cv2.pyrUp 是一个上采样的过程,尽管相对尺寸变大,但是分辨率不会增加,图像会变得更模糊。
测试代码如下:
import cv2 as cv
src = cv.imread("./testimg.jpeg")
print(src.shape[:2])
cv.imshow("src", src)
# 向下采样
dst = cv.pyrDown(src)
print(dst.shape[:2])
cv.imshow("dst", dst)
# 再次向下采样
dst1 = cv.pyrDown(dst)
print(dst1.shape[:2])
cv.imshow("dst1", dst1)
cv.waitKey()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
运行代码之后,得到三张图片,大小依次减小,分辨率降低。

通过上面运行得到的最小图,在执行向上采样之后,图片会变的模糊,这也说明上采样和下采样是非线性处理,它们是不可逆的有损处理,因此下采样后的图像是无法还原的,即使放大图片也会变模糊(后面学习到拉普拉斯金字塔可以解决该问题)。
# 向上采样
dst2 = cv.pyrUp(dst1)
print(dst2.shape[:2])
cv.imshow("dst2", dst2)
- 1
- 2
- 3
- 4
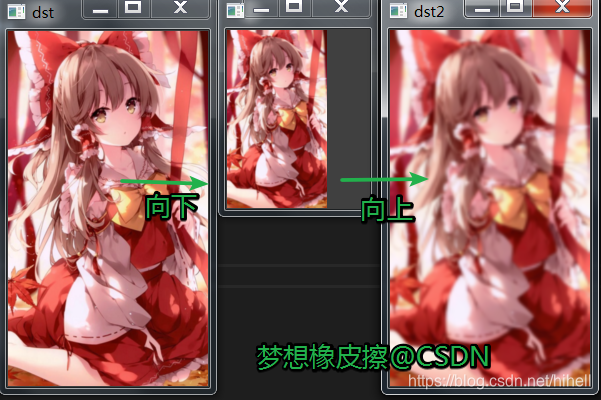
在总结一下上采样和下采样的步骤:
- 上采样:使用 cv2.pyrUp 函数, 先将图像在每个方向放大为原来的两倍,新增的行和列用 0 填充,再使用先前同样的内核与放大后的图像卷积,获得新增像素的近似值;
- 下采样:使用 cv2.pyrDown 函数,先对图像进行高斯内核卷积 ,再将所有偶数行和列去除。
拉普拉斯金字塔(Laplacian Pyramid, LP)
拉普拉斯金字塔主要用于重建图像,由上文我们已经知道在使用高斯金字塔的的时候,上采样和下采样会导致图像细节丢失。
拉普拉斯就是为了在放大图像的时候,可以预测残差,何为残差,即小图像放大的时候,需要插入一些像素值,在上文直接插入的是 0,拉普拉斯金字塔算法可以根据周围像素进行预测,从而实现对图像最大程度的还原。
学习到原理如下:用高斯金字塔的每一层图像,减去其上一层图像上采样并高斯卷积之后的预测图像,得到一系列的差值图像即为 LP 分解图像(其中 LP 即为拉普拉斯金字塔图像)。
关于拉普拉斯还存在一个公式(这是本系列课程第一次书写公式),其中 L 为拉普拉斯金字塔图像,G 为高斯金字塔图像
L n = G n − P y r U p ( P y r D o w n ( G n ) ) L_n = G_n-PyrUp(PyrDown(G_n)) Ln=Gn−PyrUp(PyrDown(Gn))
使用下面的代码进行测试。
import cv2 as cv
src = cv.imread("./testimg.jpeg")
print(src.shape[:2])
cv.imshow("src", src)
# 向下采样一次
dst = cv.pyrDown(src)
print(dst.shape[:2])
cv.imshow("dst", dst)
# 向上采样一次
dst1 = cv.pyrUp(dst)
print(dst1.shape[:2])
cv.imshow("dst1", dst1)
# 计算拉普拉斯金字塔图像
# 原图 - 向上采样一次的图
laplace = cv.subtract(src, dst1)
cv.imshow("laplace", laplace)
cv.waitKey()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
运行结果如下,相关的图像已经呈现出来,重点注意最右侧的图片。
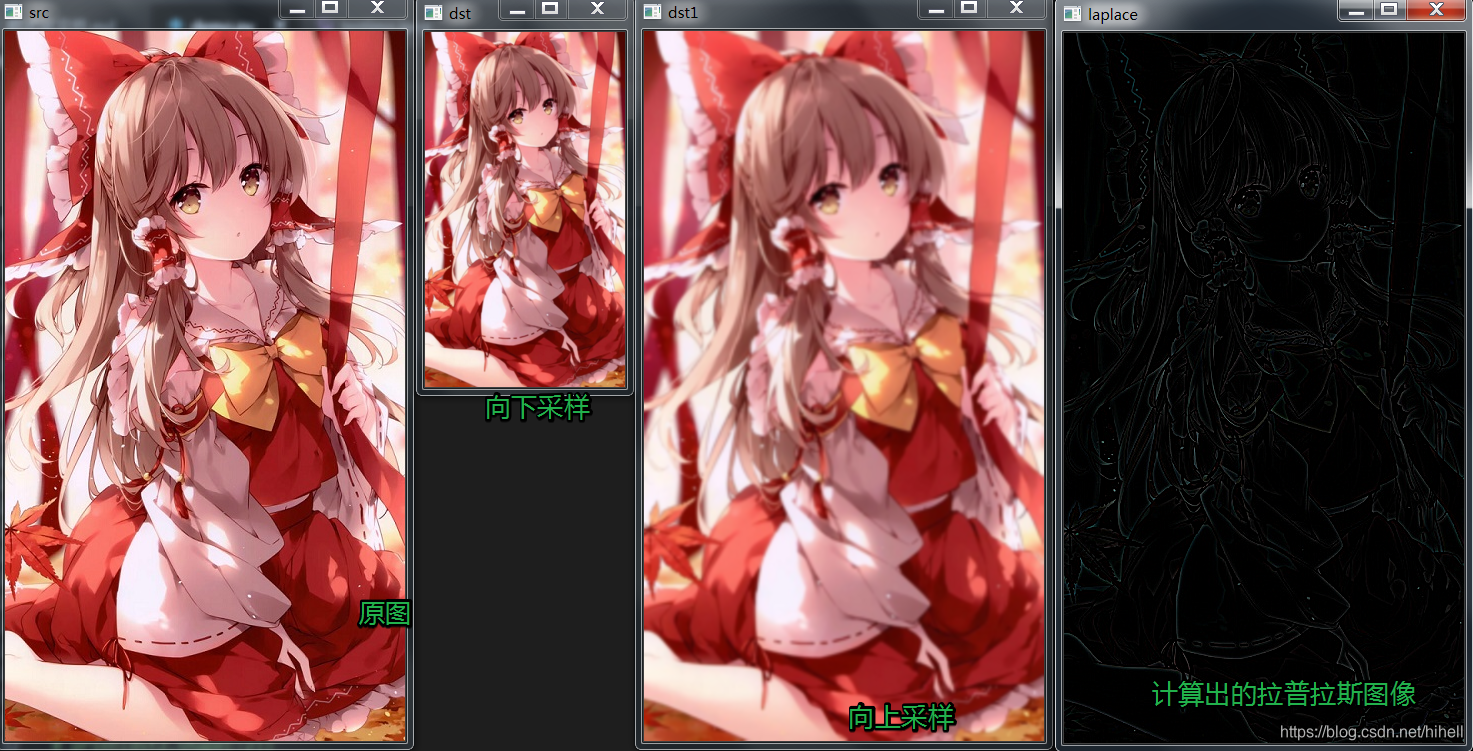
这个地方需要注意下,如果你使用 cv.subtract(src, dst1) 函数,得到的是上图效果,但是在使用还原的时候会发现问题,建议直接使用 -完成,匹配公式,修改代码如下:
# cv.subtract(src, dst1)
laplace = src - dst1
- 1
- 2
代码运行效果如下。

学习过程中发现这样一段话:图像尺寸最好是 2 的整次幂,如 256,512 等,否则在金字塔向上的过程中图像的尺寸会不等,这会导致在拉普拉斯金字塔处理时由于不同尺寸矩阵相减而出错。
这个我在实测的时候发现确实如此,例如案例中使用的图像,在向下采样 2 次的时候,图像的尺寸就会发生变化,测试代码如下:
import cv2 as cv
src = cv.imread("./testimg.jpeg")
print(src.shape[:2])
cv.imshow("src", src)
# 向下采样1次
dst1 = cv.pyrDown(src)
print(dst1.shape[:2])
cv.imshow("dst", dst1)
# 向下采样2次
dst2 = cv.pyrDown(dst1)
print(dst1.shape[:2])
cv.imshow("dst2", dst2)
# 向上采样1次
up_dst1 = cv.pyrUp(dst2)
print(up_dst1.shape[:2])
cv.imshow("up_dst1", up_dst1)
# 计算拉普拉斯金字塔图像
# 采样1次 - 向上采样1次的图
laplace = dst1 - up_dst1
cv.imshow("laplace", laplace)
cv.waitKey()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
注意 print(up_dst1.shape[:2]) 部分的输出如下:
(710, 400)
(355, 200)
(355, 200)
(356, 200)
- 1
- 2
- 3
- 4
如果在该基础上使用拉普拉斯图像金字塔,就会出现如下错误
Sizes of input arguments do not match
- 1
在总结一下拉普拉斯图像金字塔的执行过程:
- 向下采样:用高斯金字塔的第 i 层减去 i+1 层做上采样的图像,得到拉普拉斯第 i 层的图像;
- 向上采样:用高斯金字塔的 i+1 层向上采样加上拉普拉斯的第 i 层,得到第 i 层的原始图像。
向下采样上面的代码已经实现了,但是拉普拉斯向上采样还未实现,完善一下代码如下,为了代码清晰,我们将变量命名进行修改。
import cv2 as cv
src = cv.imread("./testimg_rect.jpeg")
print(src.shape[:2])
cv.imshow("src", src)
# 高斯金字塔第 0 层
gus0 = src # 原图
# 高斯金字塔第 1 层
gus1 = cv.pyrDown(gus0)
# 高斯第 2 层
gus2 = cv.pyrDown(gus1)
# 拉普拉斯金字塔第 0 层
lap0 = gus0 - cv.pyrUp(gus1)
# 拉普拉斯金字塔第 1 层
lap1 = gus1 - cv.pyrUp(gus2)
# 显示拉普拉斯第一层代码
cv.imshow("laplace", lap1)
cv.waitKey()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
下面用修改好的代码完成还原图片的操作。
import cv2 as cv
src = cv.imread("./testimg_rect.jpeg")
print(src.shape[:2])
cv.imshow("src", src)
# 高斯金字塔第 0 层
gus0 = src # 原图
# 高斯金字塔第 1 层
gus1 = cv.pyrDown(gus0)
# 高斯第 2 层
gus2 = cv.pyrDown(gus1)
# 拉普拉斯金字塔第 0 层
lap0 = gus0 - cv.pyrUp(gus1)
# 拉普拉斯金字塔第 1 层
lap1 = gus1 - cv.pyrUp(gus2)
rep = lap0 + cv.pyrUp(lap1 + cv.pyrUp(gus2))
gus_rep = cv.pyrUp(cv.pyrUp(gus2))
cv.imshow("rep", rep)
cv.imshow("gus_rep", gus_rep)
cv.waitKey()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
以上代码最重要的部分为下面两句:
rep = lap0 + cv.pyrUp(lap1 + cv.pyrUp(gus2))
gus_rep = cv.pyrUp(cv.pyrUp(gus2))
- 1
- 2
第一行代码中 lap1 + cv.pyrUp(gus2) 即文字公式 【用高斯金字塔的 i+1 层向上采样加上拉普拉斯的第 i 层,得到第 i 层的原始图像】的翻译。
第二行代码是使用直接向上采样,最终得到的是损失细节的图像。
上述代码运行的结果如下,通过拉普拉斯可以完美还原图像。
学习本案例之后,你可以在复盘本文开始部分的代码,将其进行修改。

最后在学习一种技巧,可以直接将两幅图片呈现,代码如下:
import cv2 as cv
import numpy as np
src = cv.imread("./testimg_rect.jpeg")
print(src.shape[:2])
cv.imshow("src", src)
# 向下采样1次
down_dst1 = cv.pyrDown(src)
print(down_dst1.shape[:2])
cv.imshow("dst", down_dst1)
# 向上采样1次
up_dst1 = cv.pyrUp(down_dst1)
print(up_dst1.shape[:2])
cv.imshow("up_dst1", up_dst1)
res = np.hstack((up_dst1, src))
cv.imshow('res', res)
cv.waitKey()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
运行之后,通过 np.hstack((up_dst1, src))函数,将两个图像矩阵合并,实现效果如下:

橡皮擦的小节
希望今天的 1 个小时,你有所收获,我们下篇博客见~
相关阅读
技术专栏
逗趣程序员
今天是持续写作的第 71 / 100 天。
如果你有想要交流的想法、技术,欢迎在评论区留言。
如果你想跟博主建立亲密关系,可以关注同名公众号 梦想橡皮擦,近距离接触一个逗趣的互联网高级网虫。
博主 ID:梦想橡皮擦,希望大家点赞、评论、收藏。
文章来源: blog.csdn.net,作者:梦想橡皮擦,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/hihell/article/details/113484961
- 点赞
- 收藏
- 关注作者


评论(0)