【深度学习基础-06】支持向量机SVM（下）-线性不可分

 1 SVM的优点

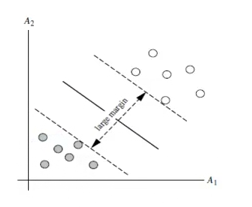
训练好的模型算法复杂度是由支持向量的个数决定，而不是数据维度决定，所以SVM不太容易过拟合。

SVM训练出来的模型完全依赖于支持向量，即使训练集里面所有非支持点都去除，重复训练过程，结果模型完全一样

一个SVM如果训练得到的支持向量个数少，则模型更容易泛化（比如各有1个点，剩下的所有可以随便扔）

2 针对线性不可分情况

数据集在空间中对应的向量不可以被一个超平面分开

2.1 如何解决？

1. 利用一个非线性的映射，把原数据集中的向量点转化到更高维度的空间中
2. 在这个高纬度空间找一个线性超平面来根据线性可分的情况处理

举例子：一维度转化为两个维度

文章来源: kings.blog.csdn.net，作者：人工智能博士，版权归原作者所有，如需转载，请联系作者。

原文链接：kings.blog.csdn.net/article/details/86101273