时间序列分析-------乘法季节模型

推荐阅读

1. 使用Python完成时间序列分析基础
2. SPSS建立时间序列乘法季节模型实战案例
3. SPSS建立时间序列加法季节模型实战案例
4. Python建立时间序列ARIMA模型实战案例

• 乘法季节模型结构

乘法季节模型建立

绘制时序图

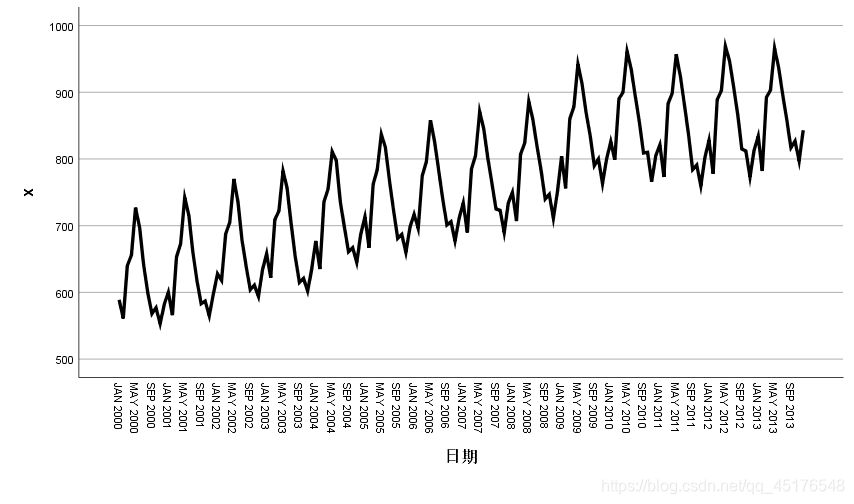
时序图显示该序列具有长期增长性趋势和以年为周期的季节效应

差分平稳化

        对原序列做1阶12步差分，希望提取原序列的趋势效应和季节效应，差分后的时序图如下所示： 

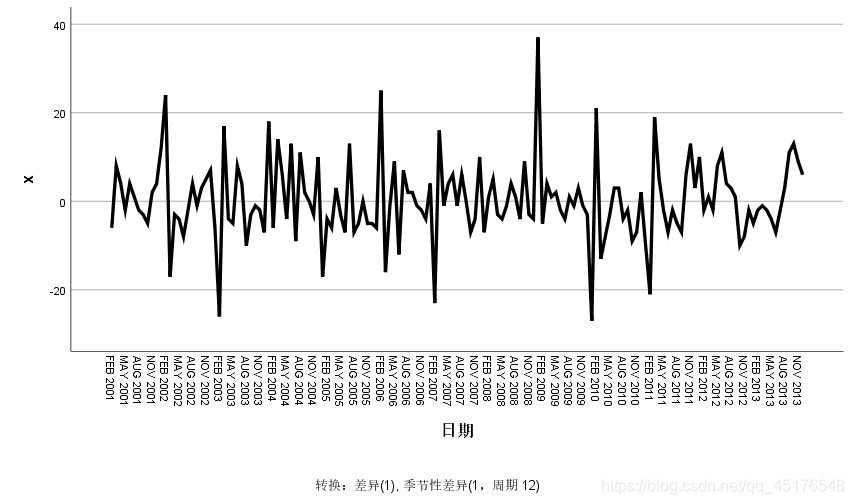
易得模型平稳

白噪声检验

 P<α，故拒绝原假设，即差分后的序列属于非白噪声序列

 综上：差分后的序列是平稳非白噪声序列，需要对差分后的序列进一步拟合ARMA模型

时序图定阶

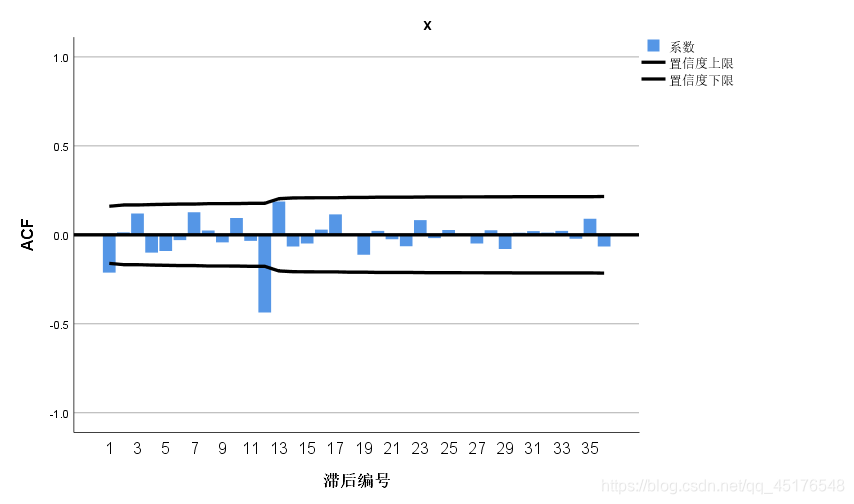
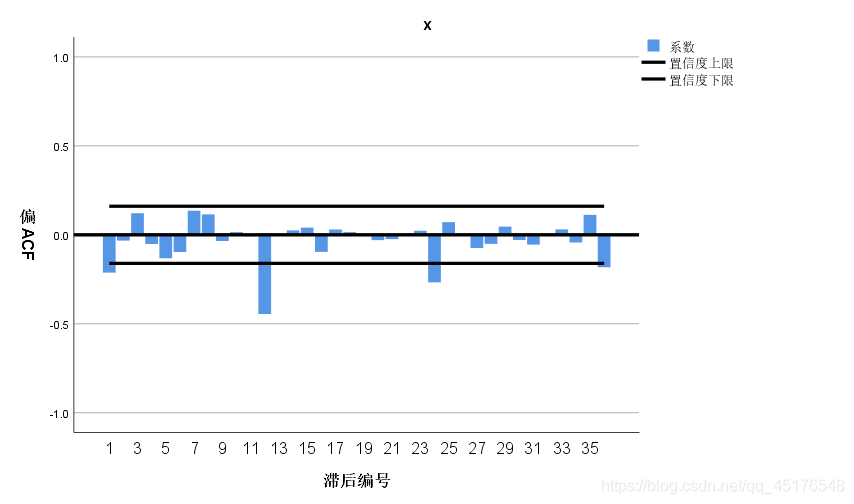
自相关图显示延迟12阶自相关系数大于两倍标准差，这说明差分后序列中仍然蕴含非常显著的季节效应，延迟1阶的自相关系数也大于2倍标准差，这说明差分后序列还具有短期相关性。     

1. 短期相关特征：自相关图和偏自相关图显示12阶以内的自相关系数，ARMA(1,1),ARMA(1,0),ARMA(0,1)提取差分后序列的短期自相关信息
2. 季节自相关特征：季节自相关特征时自相关系数截尾，偏自相关系数拖尾，这里可以永12步为周期的ARMA(0,1)12模型来提取差分后序列的季节自相关信息。

参数估计和模型检验

综合前面的差分信息，我们要建立ARIMA(1,1,1)*(0,1,1)12、ARIMA(1,1,0)*(0,1,1)12、ARIMA(0,1,1)*(0,1,1)12模型

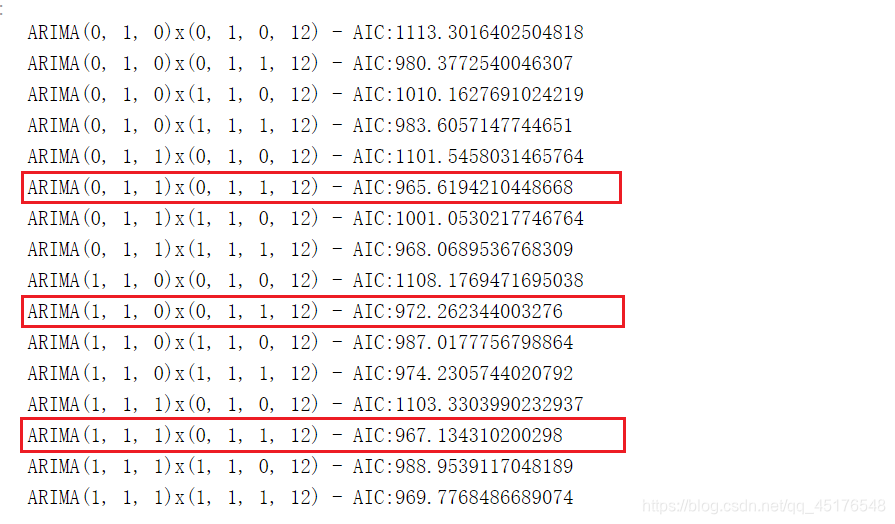
• ARIMA(1,1,1)*(0,1,1)12

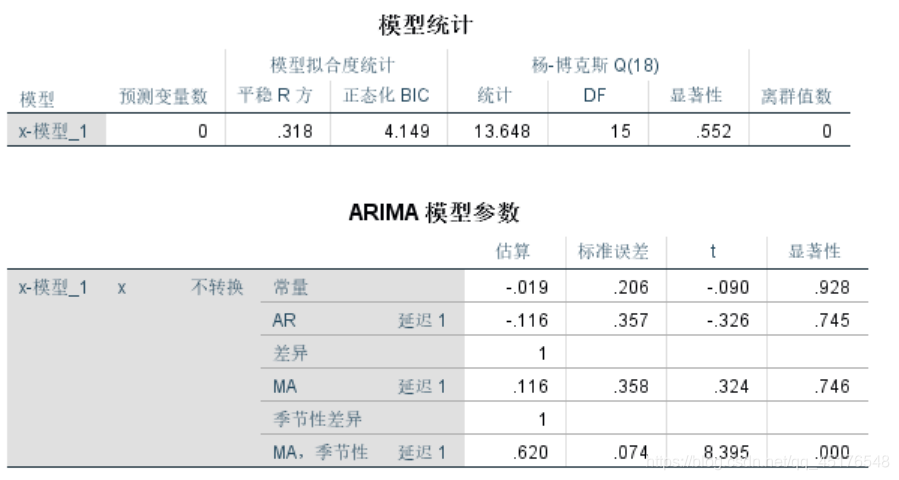
 P<α，参数的显著性不通过检验

• ARIMA(0,1,1)*(0,1,1)12

模型的显著性检验：

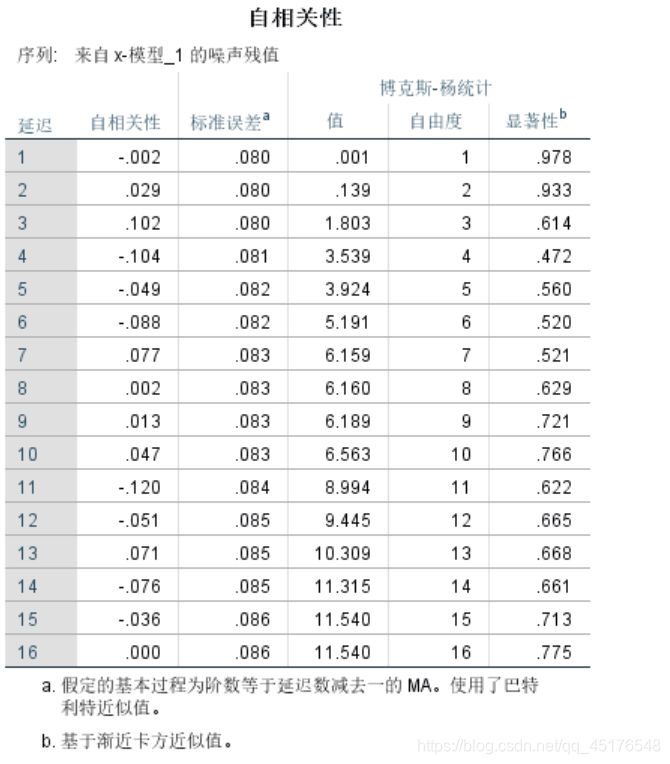
建立模型：

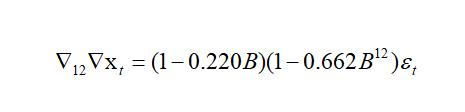
• ARIMA(1,1,0)*(0,1,1)12

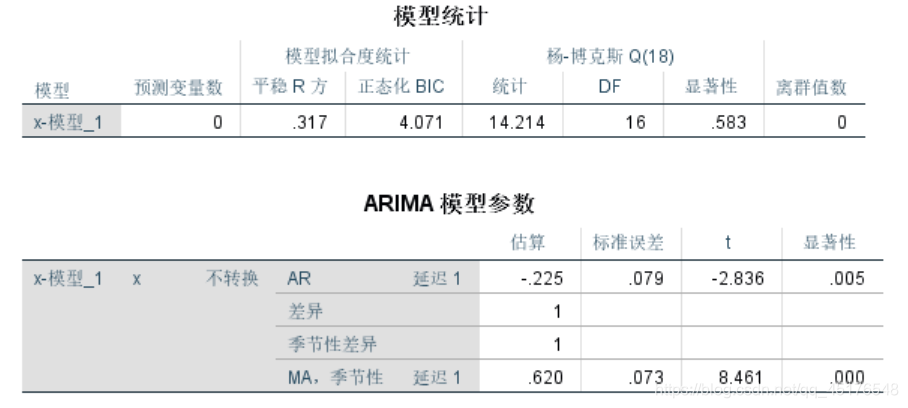
                                                                                                                      参数的显著性检验通过

模型的显著性检验

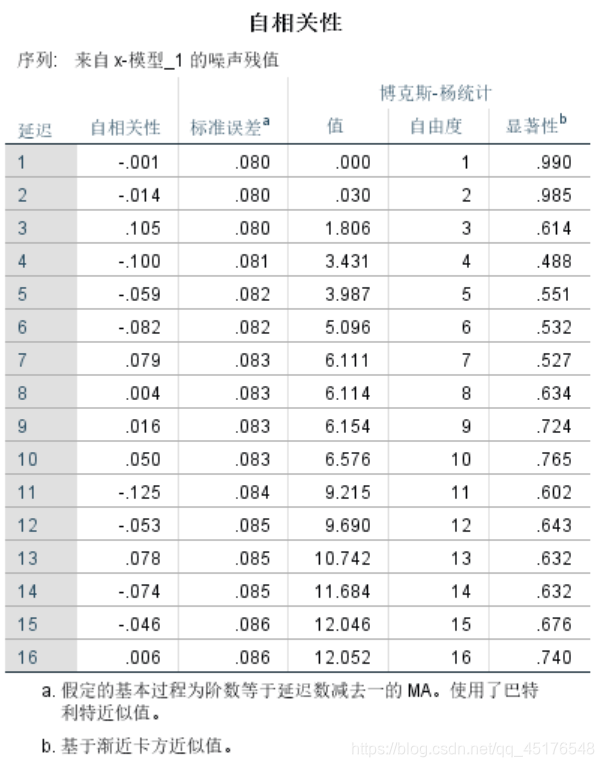
建立模型：

模型预测

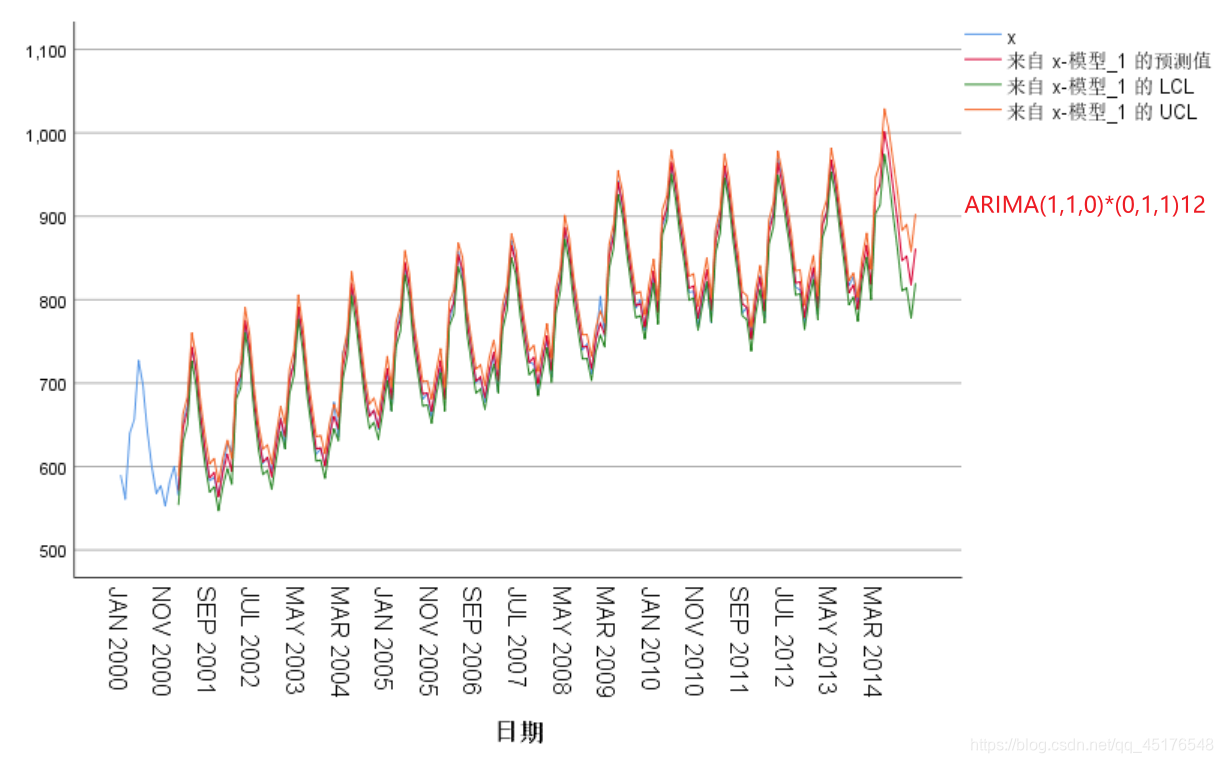
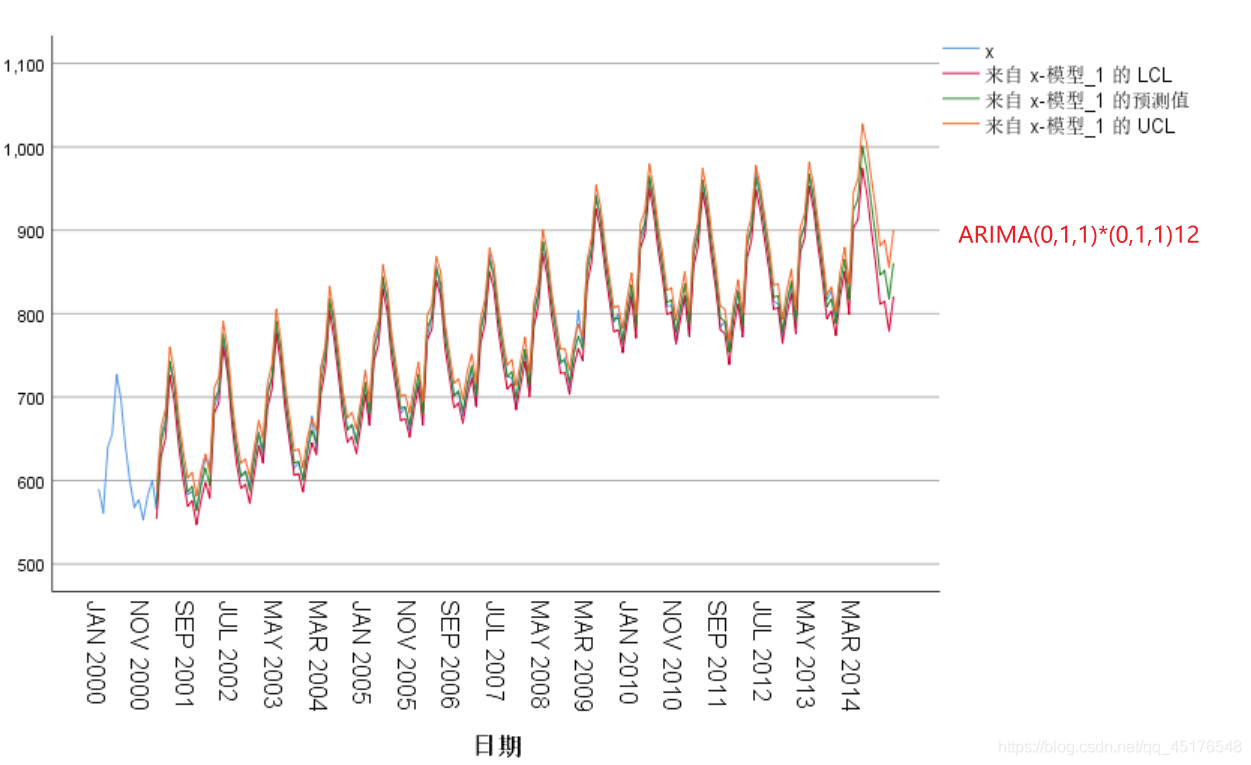
> 到这里就结束了，如果对你有帮助你，欢迎点赞关注，你的点赞对我很重要

文章来源: blog.csdn.net，作者：北山啦，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/qq_45176548/article/details/111416495