ResNet模型解析

从2012年开始，卷积神经网络（Convolutional Neural Networks, CNN）极速发展，不断涌现出诸如AlexNet、VGGNet等优秀的神经网络。到了2015年，一个新型的网络更是颠覆了计算机视觉领域和深度学习领域，这就是ResNet。

ResNet（Residual Neural Network）由微软研究院的何凯明等四名华人提出，其论文《Deep Residual Learning for Image Recognition》一举摘得CVPR2016最佳论文，下图就是它在 ILSVRC 和 COCO 2015 上的战绩。

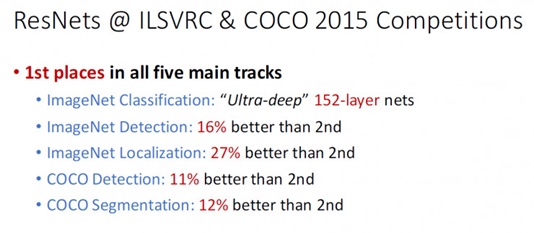
残差学习

人们在探索深度学习网络的过程中，发现了“网络越深，效果越好”这一规律，从Alexnet的7层发展到了VGG的16乃至19层。然而在继续加深网络的时候遇到了问题：

• 网络越深，模型训练难度越大，收敛速度变得很慢；

• 当网络深度达到一定深度的时候，模型的效果很难再提升；

• 甚至在继续增加深度时出现错误率提高的情况。

出现这样类似“退化”的问题，主要是由于网络深度的增加，带来的在网络训练的时候，梯度无法有效的传递到浅层网络，导致出现梯度弥散（vanishing）。何凯明等人提出的残差结构就很好地解决了这个问题。残差的基本结构如下图所示：

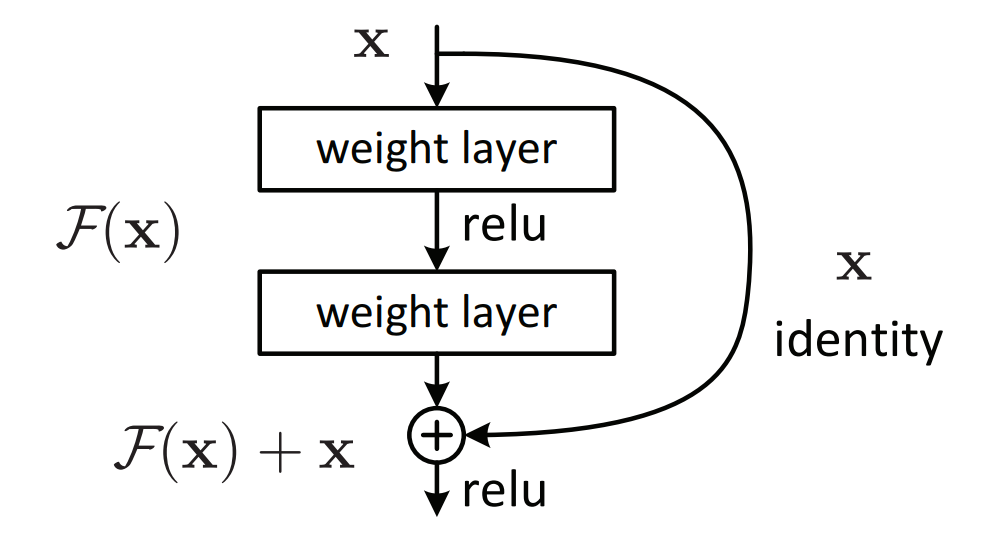
这有点类似与电路中的“短路”，所以是一种短路连接（shortcut connection），该残差块也被称为shortcut。它的原理是：对于一个堆积层结构（几层堆积而成）当输入为 x 时，其学习到的特征记为 H(x) ，现在我们希望其可以学习到残差 F(x)=H(x)-x ，这样其实原始的学习特征是 F(x)+x 。之所以这样是因为残差学习相比原始特征直接学习更容易。当残差为 0 时，此时堆积层仅仅做了恒等映射，至少网络性能不会下降，实际上残差不会为 0，这也会使得堆积层在输入特征基础上学习到新的特征，从而拥有更好的性能。

总的来看，该层的神经网络可以不用学习整个的输出，而是学习上一个网络输出的残差，因此ResNet又叫做残差网络。

ResNet网络结构

作者为了表明残差网络的有效性，使用如下三种网络进行对比。

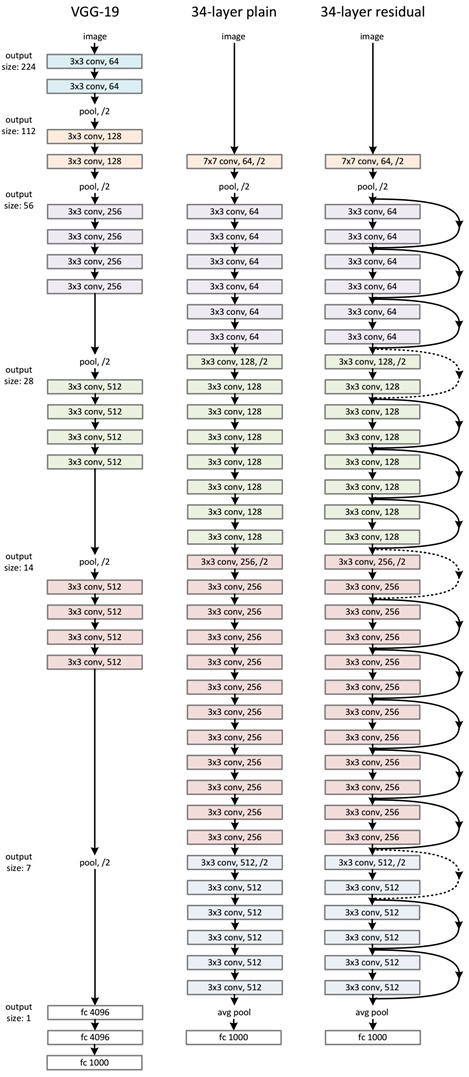
其一为 VGG-19 网络（这是 VGG paper 中最深的亦是最有效的一种网络结构），另外则是顺着VGG网络思路继续简单地加深层次而形成的一种 VGG 朴素网络，它共有34个含参层。最后则是与上述34层朴素网络相对应的 Resnet 网络，由前面介绍的残差单元来构成。在论文中可以看到详细的实验对比结果，ResNet 的结构可以极快的加速神经网络的训练，收敛性能好；模型的准确率有比较大的提升，分类性能好。

在 ResNet 中的网络结构单元被称为模块——block，其中会用到两种残差模块：一种是以两个 3x3 的卷积网络串接在一起作为一个残差模块，用于34-layer；另外一种，考虑到实际计算的时间和效率问题，作者提出了命名为 bottleneck 的结构块来代替常规的 Resedual block，将 1x1 、3x3、1x1 的3个卷积网络串接在一起作为一个残差模块，常用于层数更多的网络中。如下图所示。

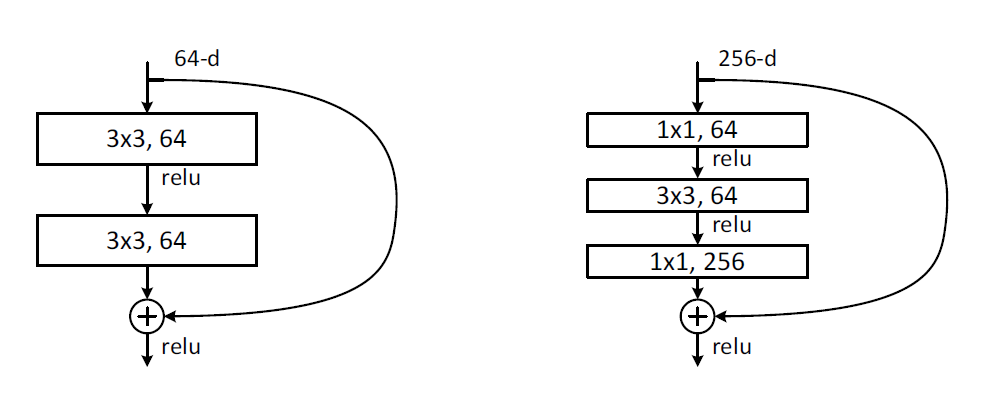
除上面展示的34-layer的ResNet，还可以构建更深的网络，如下表所示。

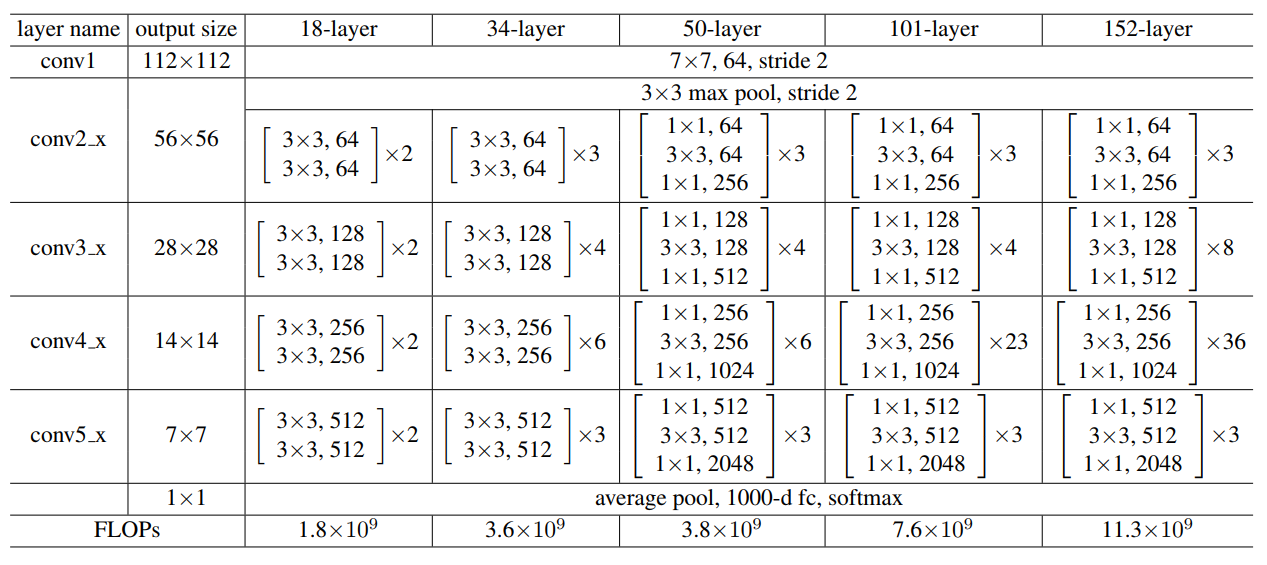
上面一共提出了5种深度的ResNet，分别是18，34，50，101和152。比较常用的是50-layer，101-layer，152-layer。他们都是由上述的残差模块堆叠在一起实现的。在此以ResNet50为例，拆解其结构，使读者有更直观的了解。

在Keras中，ResNet50的网络的整体结构示例为:

data  1,3,224,224

conv  filter=64, kernel_size=7, pad=3,stride=2 1,64,112,112

bn
activation('relu')

maxpool kernel_size=3,stride=2  1,64,56,56

# block 1  (64,64,256)
conv_block() in:1,64,56,56 filter=(64,64,256),out=1,256,56,56
identity_block  in=1,256,56,56, filter=(64,64,256),out=1,256,56,56
identity_block  in=1,256,56,56, filter=(64,64,256),out=1,256,56,56

# block 2  (128,128,512)
conv_block  in=1,256,56,56 filter=(128,128,512),out=1,512,28,28
identity_block  in=1,256,56,56 filter=(128,128,512),out=1,512,28,28
identity_block  in=1,256,56,56 filter=(128,128,512),out=1,512,28,28
identity_block  in=1,256,56,56 filter=(128,128,512),out=1,512,28,28

# block 3 (256,256,1024)
conv_block  in=1,512,28,28 filter=(256,256,1024),out=1,1024,14,14
identity_block  in=1,512,28,28 filter=(256,256,1024),out=1,1024,14,14
identity_block  in=1,512,28,28 filter=(256,256,1024),out=1,1024,14,14
identity_block  in=1,512,28,28 filter=(256,256,1024),out=1,1024,14,14
identity_block  in=1,512,28,28 filter=(256,256,1024),out=1,1024,14,14
identity_block  in=1,512,28,28 filter=(256,256,1024),out=1,1024,14,14

# block 4 (512,512,2048)
conv_block  in=1,1024,14,14 filter=(512,512,2048),out=1,2048,7,7
identity_block  in=1,1024,14,14 filter=(512,512,2048),out=1,2048,7,7
identity_block  in=1,1024,14,14 filter=(512,512,2048),out=1,2048,7,7

maxpool kernel_size=7, stride=1 out=1,2048,1,1

flatten

dence(1,1000)

acivation('softmax')

probbility(1,1000)

在Keras代码中定义该网络模型，如下：

def resnet_model(out_class, input_shape):

    inputs = Input(shape=input_shape) #1,3,224,224

    #
    x = Conv2D(64, (7, 7), strides=2, padding='same')(inputs) #conv1  1,64,112,112
    x = BatchNormalization(axis=-1)(x) #bn_conv1
    x = Activation('relu')(x) #conv1_relu

    x = MaxPool2D(pool_size=(3,3),strides=2)(x) # 1,64,56,56

    # block1  (64,64,256) 1,2 in:1,64,56,56
    x = conv_block(x, [64, 64, 256]) #out=1,256,56,56
    x = identity_block(x, [64, 64, 256]) #out=1,256,56,56
    x = identity_block(x, [64, 64, 256]) #out=1,256,56,56

    # block2  (128,128,512) 1,3 in:1,256,56,56
    x = conv_block(x, [128,128,512]) #out=1,512,28,28
    x = identity_block(x, [128,128,512]) #out=1,512,28,28
    x = identity_block(x, [128,128,512]) #out=1,512,28,28
    x = identity_block(x, [128, 128, 512])  # out=1,512,28,28

    # block 3 (256,256,1024) 1,5 in:1,512,28,28
    x = conv_block(x, [256,256,1024])  # out=1,1024,14,14
    x = identity_block(x, [256, 256, 1024])  # out=1,1024,14,14
    x = identity_block(x, [256, 256, 1024])  # out=1,1024,14,14
    x = identity_block(x, [256, 256, 1024])  # out=1,1024,14,14
    x = identity_block(x, [256, 256, 1024])  # out=1,1024,14,14
    x = identity_block(x, [256, 256, 1024])  # out=1,1024,14,14

    # block 4 (512,512,2048) 1,2 in:1,1024,14,14
    x = conv_block(x, [512,512,2048])  # out=1,2048,7,7
    x = identity_block(x, [512, 512, 2048])  # out=1,2048,7,7
    x = identity_block(x, [512, 512, 2048])  # out=1,2048,7,7

    # maxpool kernel_size=7, stride=1 out=1,2048,1,1
    x = MaxPool2D(pool_size=(7, 7), strides=1)(x)

    # flatten
    x = Flatten()(x)

    # Dense
    x = Dense(classes, activation='softmax')(x) # out=1,1000

    model = Model(inputs=inputs, outputs=out)

    return model

下面是一些ResNets的其他特征：

• 网络较深，控制了参数数量。

• 存在明显层级，特征图个数层层递进，保证输出特征的表达能力。

• 使用较少池化层，大量采用下采样，提高传播效率。

• 没有使用 dropout，利用 Batch Normalization 和全局平均池化进行正则化，加快训练速度。

• 层数较高时减少了3x3卷积核的个数，用1x1卷积核控制3x3卷积的输入输出特征 map 的数量。

深度残差网络的提出是CNN图像史上的一件里程碑事件，随着对其的不断深入研究，有很多 ResNet 的变体已经出现，如：ResNeXt、DenseNet、WideResNet等，有待读者继续深入关注和了解。