神经网络的学习笔记

一、神经网络概述

神经网络是深度学习的重要的工具，其本身是机器学习的一个算法，主要用于解决复杂的AI问题，包括卷积神经网络（CNN），全连接神经网络（FNN），循环神经网络（RNN）等。神经网络算法复杂，涉及的原理较多也较难，包括参数的迭代更新，激活函数，损失函数，梯度消失，反向传播等，下面将列出个人对于这些知识点的见解，仅供参考，也欢迎大佬指正。

二、神经网络的工作流程

神经网络分为输入层、隐藏层和输出层，输入层负责接收我们喂进模型的数据，隐藏层对数据进行学习后给出预测，输出层将预测的结果输出，明显可以看出神经网络的关键在于隐藏层的设计。一般来讲隐藏层会对来自上一层的数据进行一个线性的映射，即y(x)=w*x+b，得到新的特征，再经过激活函数将线性的结果转化为非线性的结果再传给下一层神经网络，而下一层的神经网络再做同样的工作，只是参数w和b不同，待经过所有的神经网络后得出一个预测值，将其与真实值比较并计算损失函数，根据损失函数的大小进行反向传播，对参数进行更新。

三、几个比较难的点

1.激活函数

上面也有提到，激活函数是将线性的结果进行非线性转化，即是将线性的结果映射到激活函数中，以提高模型的泛化能力，目前较多的是使用Relu函数作为激活函数，在这之前的激活函数有Sigmoid函数等。
Sigmoid函数图像：

Sigmoid: $S(x)=1/(1+e^{-x})$
Relu函数的图像：

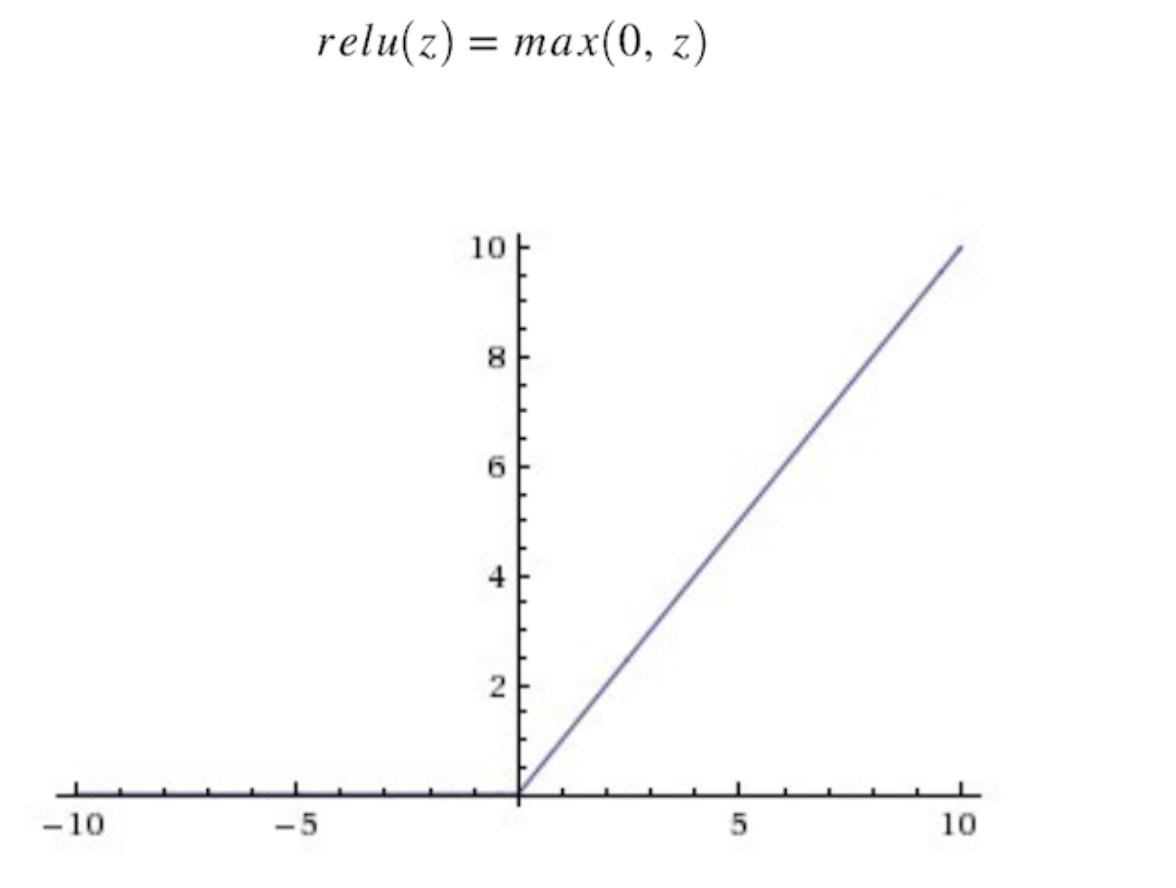
至于为什么要将Sigmoid换成Rule的问题将在下一个点解释。

2.反向传播和梯度下降

在神经网络的流程中我们知道每一层神经网络的参数w和b是需要更新的，而更新发生在反向传播的过程中，在每一次的学习后神经网络将预测值与真实值进行对比计算出损失函数，接下来损失函数对上一层的参数进行求导得出梯度的方向，根据梯度的反方向进行参数更新（之所以用梯度的方向，是因为梯度的方向变化得最快），更新的步长称为学习率，这种参数优化的方法叫做梯度下降，这一层参数更新完成后，再对上一层的参数进行求导，之后还是一样的流程，直到第一层的参数更新完毕，整个过程即为反向传播。
由于反向传播直接是对结果的链式求导，因此上文提到的激活函数对参数更新时梯度的计算具有极大的影响，激活函数的大小直接影响梯度的大小。对于Sigmoid函数，随着训练的次数的增加和神经网络层数的增加，Sigmoid函数的梯度接近零，会出现因为梯度消失带来的参数无法更新的问题，因此才会使用Relu函数来代替Sigmoid，当然了Relu函数也存在一定的缺陷，比如零点附近梯度突变的问题，所以也存在Relu函数的衍生形式的激活函数。

3.Drop_out

Drop_out是神经网络中随机丢弃某些神经元的操作。由于神经网络模型是基于对训练数据的训练得到的，所以在对训练数据的拟合会有一个不错的效果，但有时候我们训练后得到的模型对于测试数据的拟合效果不佳，说明模型出现了过拟合现象，泛化能力不足，因此我们在测试的时候随机丢弃一些神经元，降低模型对训练数据的依赖，降低其过拟合的可能性，不过这里的丢弃并非是真正的将神经元删除，而只是在喂进测试数据时不通过某个神经元的映射而已，即只是切断了“通路”，原本的模型并不发生改变。