前期我们对机器学习的基础知识，从基础的概念到实用的代码实战演练，并且系统的了解了机器学习在分类算法上面的应用，同时也对机器学习的准备知识有了一个相当大的了解度，而且还拓展了一系列知识，如推荐算法、文本处理、图像处理。以及交叉学科的应用，那么前期你如果认真的了解了这些知识，并加以利用和实现，相信你已经对机器学习有了一个“量”的认识，接下来的，我将带你继续学习机器学习学习，并且全方位，系统性的了解和深入机器学习领域，达到一个“质”的变化。

点击下方下载高清版学习知识图册

机器学习Python算法知识点大全，包含sklearn中的机器学习模型和Python预处理的pandas和numpy知识点

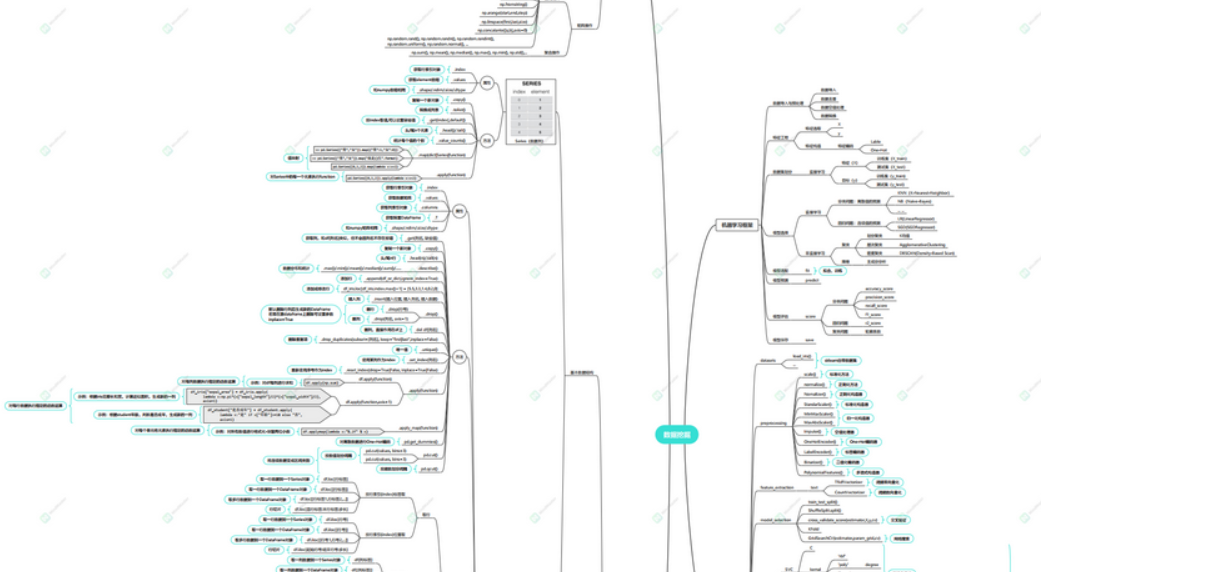
在上一篇文章，我们介绍了聚类算法以及衡量和评估聚类算法的各种方法，包括深入剖析聚类的原理，本期文章，我将带大家使用聚类进行实战

项目要求

采用聚类方法，探索最佳的聚类数N
解释你采用的方法，为什么有效（能获得最佳的聚类数目）

数据透视

代码实战

导入第三方库
from sklearn.cluster import KMeans # K均值聚类
from sklearn.cluster import AgglomerativeClustering#层次聚类
from sklearn.cluster import DBSCAN #密度聚类
from sklearn.decomposition import PCA #降维
import seaborn as sns
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
#设置字体为SimHei显示中文
plt.rcParams['font.sans-serif'] = 'SimHei'
#设置正常显示字符
plt.rcParams['axes.unicode_minus'] = False
读取数据
whw_df=pd.read_csv(r"X.csv")
whw_df.head()

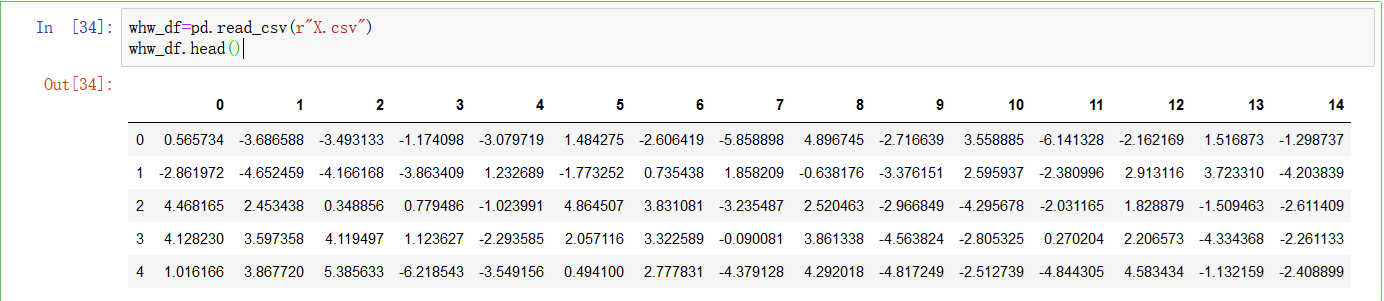
sns.pairplot(whw_df)
# 维度过多不好分析

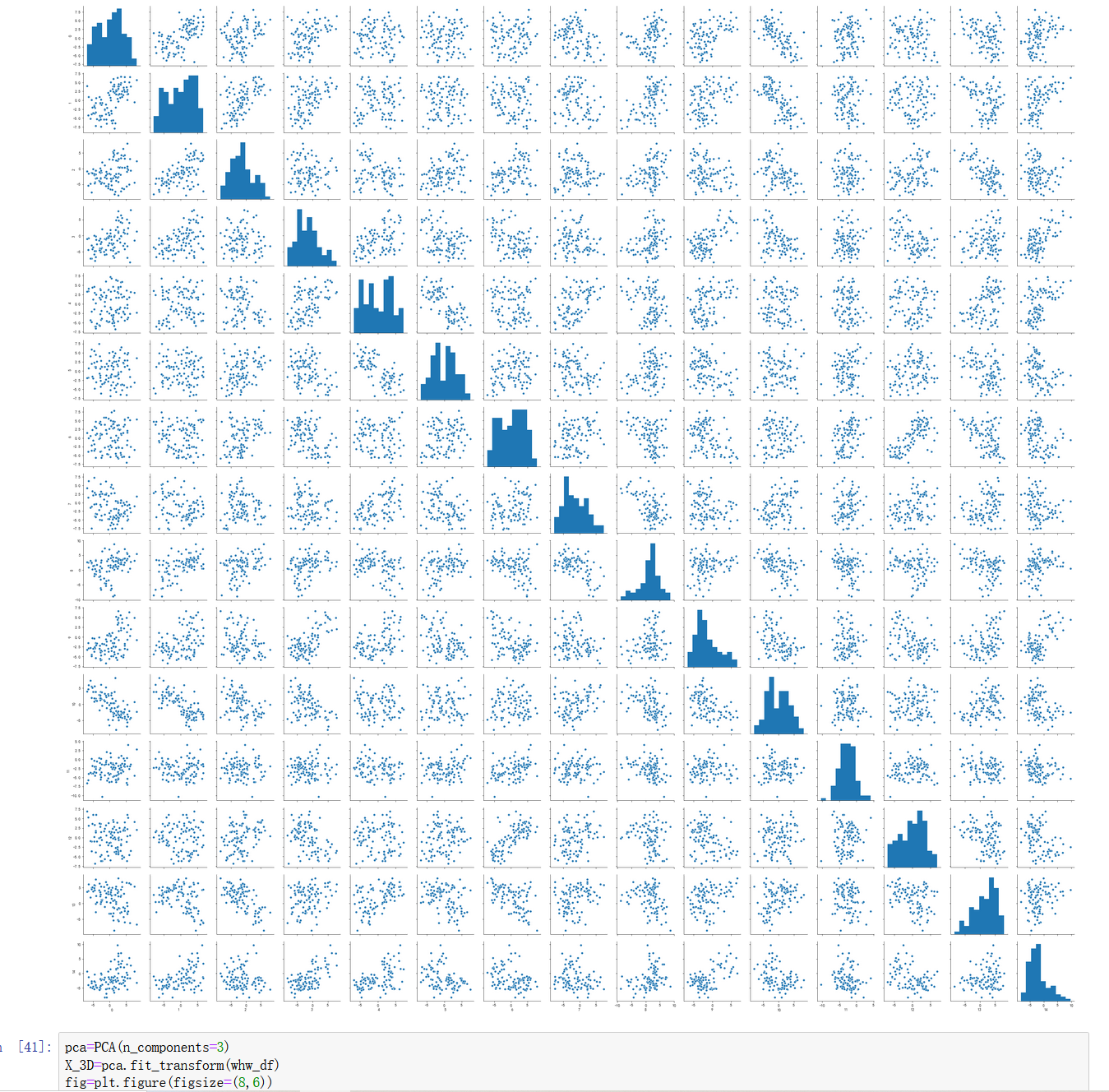
维度太多，利用PCA降维的思想进行实现（后期介绍）

#设置降至3个维度
pca=PCA(n_components=3)
X_3D=pca.fit_transform(whw_df)
fig=plt.figure(figsize=(8,6))
ax=Axes3D(fig)
#可视化
ax.scatter3D(X_3D[:,0],X_3D[:,1],X_3D[:,2],s=50)
plt.show()

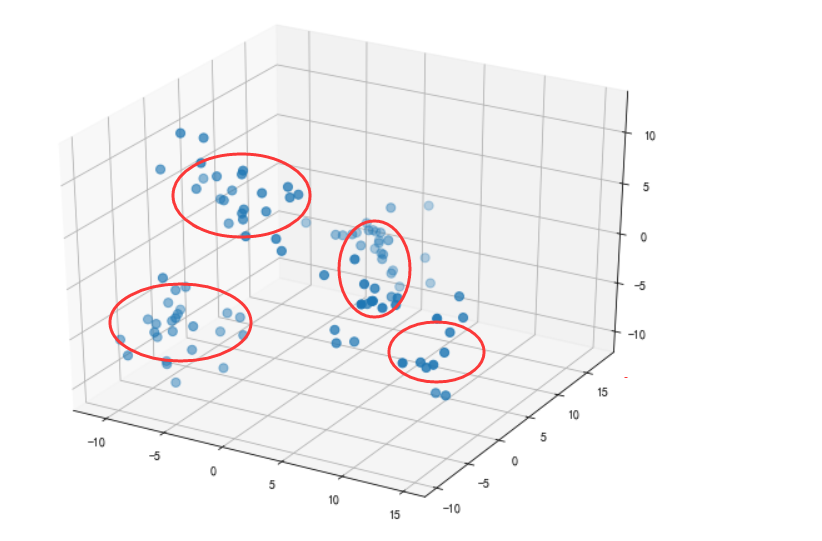
将数据降维之后，我们将其可视化绘制三维的，很容易发现呈现几个部分的聚类，这样有利于我们后续的继续探索。

寻找最佳的聚类数目（手肘法）

whw_cloumns=whw_df.columns.tolist()
# 获取列名
print(whw_cloumns)
KMeans进行选取聚类数目
分别利用手肘法和轮廓系数对聚类的数目进行探索：
手肘法
# 利用SSE选择k
whw_SSE = []  # 存放每次结果的误差平方和
for i in range(2, 8):  # 尝试要聚成的类数
    whw_estimator = KMeans(n_clusters=i)  # 构造聚类器
    whw_estimator.fit(np.array(whw_df[whw_cloumns])) #存入数组（数据的列名标签）
    whw_SSE.append(whw_estimator.inertia_)
X = range(2, 8)  # 跟k值要一样
fig = plt.figure(figsize=(8,6))
plt.xlabel('聚类数目')
plt.ylabel('SSE')
plt.plot(X, whw_SSE,'o-' )
plt.title("K值在肘关节处最优")
plt.show()  # 画出图

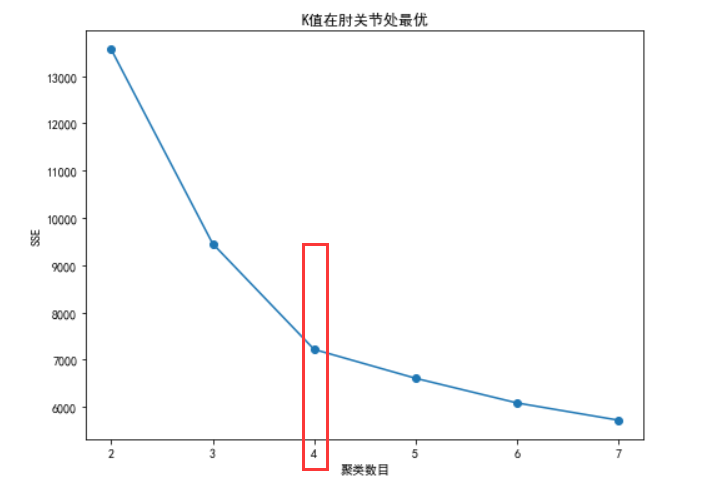
很明显在聚类数目为4的时候，比较的好，也就是拐点的地方

轮廓系数

from sklearn.metrics import silhouette_score
from sklearn.cluster import k_means
score = []
# 依次计算 2 到 7类的轮廓系数
for i in range(2,8):
    model = k_means(whw_df[whw_cloumns], n_clusters=i)
    score.append(silhouette_score(whw_df[whw_cloumns], model[1]))
fig = plt.figure(figsize=(8,6))
plt.plot(range(2, 8, 1), score,'o-')
plt.xlabel("聚类数目")
plt.ylabel("轮廓系数")
plt.title("K值在轮廓系数最高点最优")
plt.show()

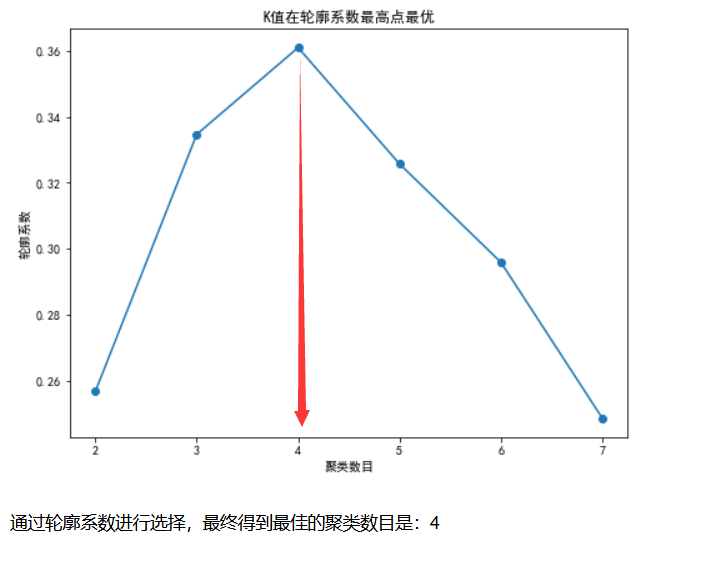
很容易发现在轮廓系数的算法里面，最佳的聚类数目也是4

可视化（对1和2标签进行可视化）

x = whw_df[[ "1","2"]]
# 建立模型
model = k_means(x, n_clusters=4)
# 绘图
plt.scatter( whw_df['1'],whw_df['2'], c=model[1])
plt.show()

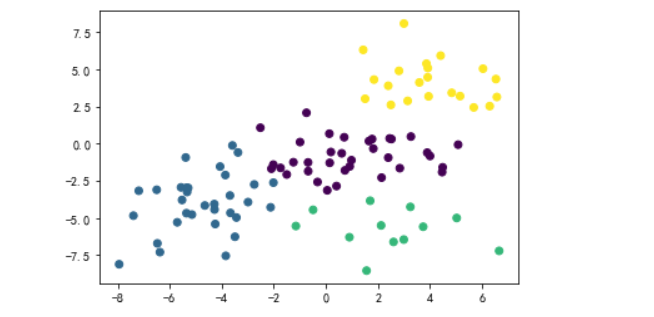
层次聚类法

import pandas as pd
import seaborn as sns  #用于绘制热图的工具包
from scipy.cluster import hierarchy  #用于进行层次聚类，话层次聚类图的工具包
from scipy import cluster   
import matplotlib.pyplot as plt
from sklearn import decomposition as skldec #用于主成分分析降维的包
whw_df_T=whw_df.T
Z = hierarchy.linkage(whw_df_T, method ='ward',metric='euclidean')
hierarchy.dendrogram(Z,labels = whw_df_T.index)

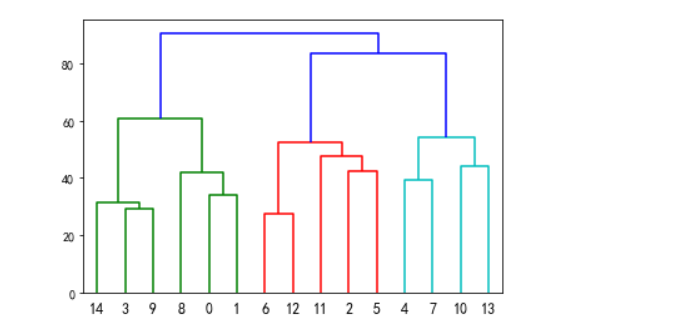
label = cluster.hierarchy.cut_tree(Z,height=57)
label = label.reshape(label.size,)
#根据两个最大的主成分进行绘图
pca = skldec.PCA(n_components = 0.95)    #选择方差95%的占比
pca.fit(whw_df_T)   #主城分析时每一行是一个输入数据
result = pca.transform(whw_df_T)  #计算结果
fig = plt.figure(figsize=(10,6))
# plt.figure()  #新建一张图进行绘制
plt.scatter(result[:, 0], result[:, 1], c=label, edgecolor='k') #绘制两个主成分组成坐标的散点图
for i in range(result[:,0].size):
    plt.text(result[i,0],result[i,1],whw_df_T.index[i])     #在每个点边上绘制数据名称
x_label = 'PC1(%s%%)' % round((pca.explained_variance_ratio_[0]*100.0),2)   #x轴标签字符串
y_label = 'PC1(%s%%)' % round((pca.explained_variance_ratio_[1]*100.0),2)   #y轴标签字符串
plt.xlabel(x_label)    #绘制x轴标签
plt.ylabel(y_label)    #绘制y轴标签

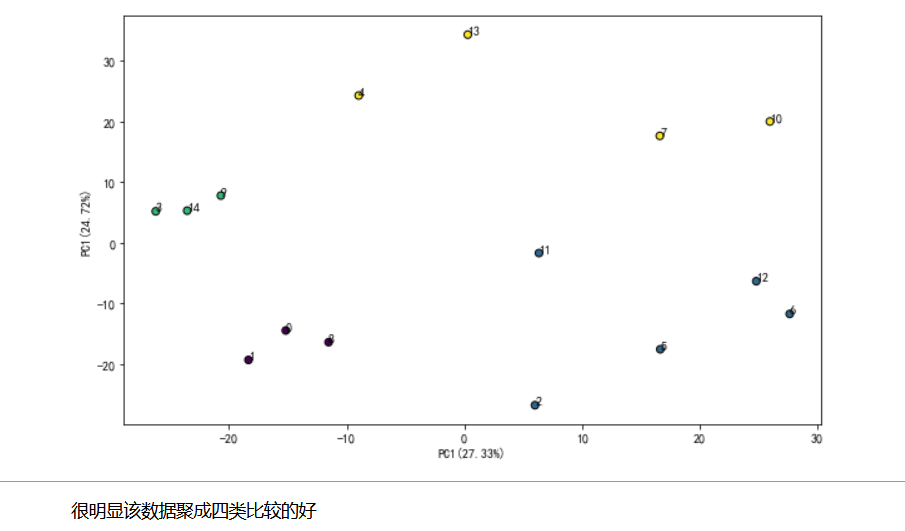
sns.clustermap(whw_df_T,method ='ward',metric='euclidean')

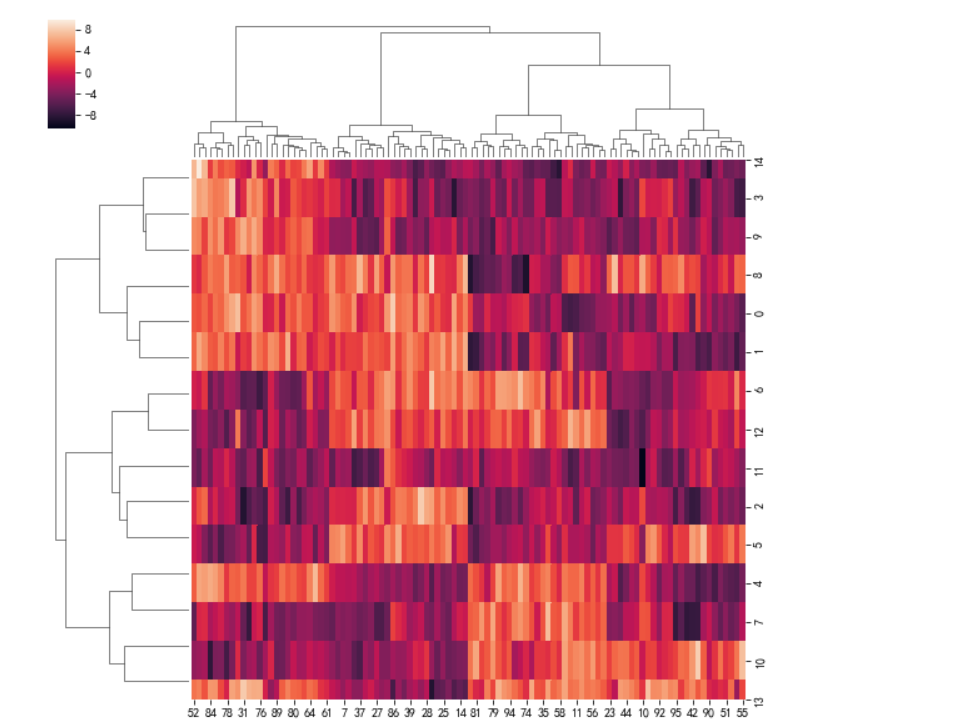
层次聚类可视化

#%% 层次聚类
from sklearn.cluster import AgglomerativeClustering
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
agg = AgglomerativeClustering(n_clusters=4,linkage='ward')
labels = agg.fit_predict(whw_df[['0','1','2']].values)
fig = plt.figure(figsize=(8,8))
ax = Axes3D(fig)
ax.scatter3D(whw_df.values[:,0],whw_df.values[:,1],whw_df.values[:,2],c=labels,s=50)
plt.show()

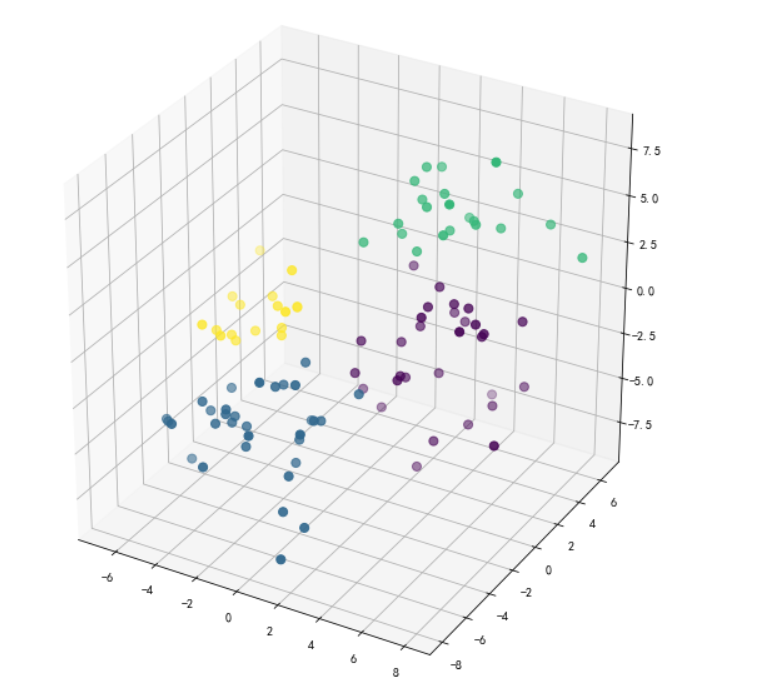通过三维指标进行聚类可视化，最终发现聚类数目为4类

密度聚类

dbs=DBSCAN()
dbs.fit_predict(whw_df)#-1代表离群点，无法分类的异常点

全部是离群点，显然不可以，我们需要调节参数进行优化，所以写循环进行测试和迭代：

report=[]
esp_range=np.arange(9,20,1)
ms_range=np.arange(8,15)
for e in esp_range:
    for ms in ms_range:
        dbs=DBSCAN(eps=e,min_samples=ms)
        y=dbs.fit_predict(whw_df)
        n_outliner=np.sum(np.where(dbs.labels_==-1,1,0))
        n_clusters=len([i for i in set(dbs.labels_) if i !=-1])
        report.append((e,ms,n_outliner,n_clusters))
pd.DataFrame(report,columns=["eps",'min_samples','n_outliner',"n_clusters"])
.plot(yticks=np.arange(0,100,5))

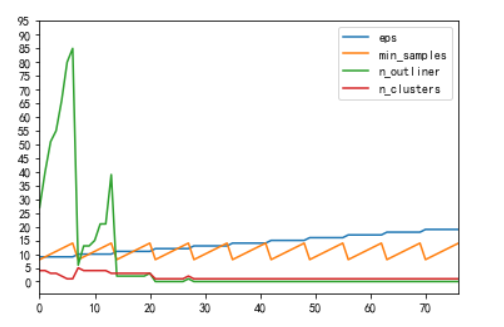
观察图形发现，参数eps最佳在10左右，min_samples在9附近
故通过测试发现，设置为下面的数值最佳


# 测试结果
dbs=DBSCAN(eps=10.5,min_samples=9)
result=dbs.fit_predict(whw_df)#-1代表离群点，无法分类的异常点
pd.value_counts(result)

离群点只有三个，已经达到较好的了

项目总结

一.K-means聚类方法

1.K-Means ( K均值）算法其中K表示簇的数量，means表示均值。算法通过预先设定的K值及每个簇的初始质心对相似的数据点进行划分。并通过划分后的均值迭代优化获得最优的聚类结果。

k值优化方案-手肘法

手肘法的核心指标是SSE(sum of the squared errors，误差平方和)

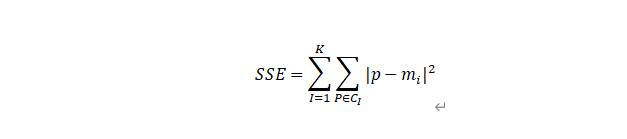
手肘法的核心思想是:随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。并且，当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说SSE和k的关系图是一个手肘的形状，而这个时部对应的k值就是数据的真实聚类数。这也是该方法被称为手时法的原因。

二．层次聚类：

层次聚类( hierarchical clustering )是指对与给定的数据集对象，我们通过层次聚类算法获得一个具有层次结构的数据集合子集结合的过程

层次聚类分为两种︰自底向上的凝聚法以及自顶向下的分裂法

2.凝聚层次聚类：
凝聚法指的是初始时将每个样本点当做一个簇，所以原始簇的数量等于样本点的个数，然后依据某种准则合并这些初始的簇，直到达到某种条件或者达到设定的簇的数目。某种准则可以是相似度

3.分裂层次聚类：
分裂法指的是初始时将所有的样本归为一个簇，然后依据某种准则进行逐渐的分裂，直到达到某种条件或者达到设定的簇的数目

三、密度聚类

DBSCAN是一种基于密度的聚类算法，这类密度聚类算法一般假定类别可以通过样本分布的紧密程度决定。同一类别的样本，他们之间的紧密相连的，也就是说，在该类别任意样本周围不远处一定有同类别的样本存在。

通过将紧密相连的样本划为一类，这样就得到了一个聚类类别。通过将所有各组紧密相连的样本划为各个不同的类别，则我们就得到了最终的所有聚类类别结果。

密度聚类(Density-Based Clustering)基于主要特点:（需要调节参数eps和min_samples）
发现任意形状的聚类

处理噪音

需要密度参数作为终止条件

DBSCAN优势：忽略噪声，发现任意形状的簇

DBSCAN的主要优点有：

可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。
可以在聚类的同时发现异常点，对数据集中的异常点不敏感。
聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。

DBSCAN的主要缺点有：

如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。
如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。
调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值ϵ
，邻域样本数阈值MinPts联合调参，不同的参数组合对最后的聚类效果有较大影响。
通过上述的K-Means ( K均值）、层次聚类、密度聚类最终得出最佳的聚类的数目为4，同时也对数据进行了探索性的尝试和研究，确定最佳的聚类数目，然后分别对其进行不同维度的测试和可视化

每文一语

已是深夜…

文章来源: wxw-123.blog.csdn.net，作者：王小王-123，版权归原作者所有，如需转载，请联系作者。

原文链接：wxw-123.blog.csdn.net/article/details/126475860

点赞
收藏
关注作者

0/1000

抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认取消

加入云驻计划，成为创作者

华为云周边好礼
免费体验产品
特殊身份标识
线下官方门票
内部专家零距离
与10000+优质创作者共同成长

立即加入

【进阶版】 机器学习之K均值聚类、层次聚类、密度聚类、实战项目含代码（15）

目录

欢迎订阅本专栏，持续更新中~

本专栏前期文章介绍！

机器学习配套资源推送

进阶版机器学习文章更新~