实现字典树
453. 最小操作次数使数组元素相等
https://leetcode.cn/problems/minimum-moves-to-equal-array-elements/

思路:
把问题换一个问法更好理解:有 n 根钉子,每次只能敲一根钉子让高度 - 1,问敲多少下钉子使得所有钉子高度一样? 答案自然就是把所有的钉子敲到跟最矮的那根一样了
根据《峡谷相对论》,当对方追着你满地图跑时,敌方加速 == 我减速,所以每次都有n-1个元素加1 == 每次都有一个元素减1。既然每次只能做减法,那么最少次数就是把所有元素都减到最小的那个元素值
class Solution {
public:
int minMoves(vector<int>& nums) {
int minVal = nums[0];//不能初始化为0,防止数组中全为负数
//1.遍历数组找到数组元素最小值
for(auto& num:nums)
{
minVal = min(minVal,num);
}
//2.所有元素到最小值需要减多少次
int res = 0;
for(auto & num:nums)
{
res+= num - minVal;
}
return res;
}
};
462. 最少移动次数使数组元素相等 II
https://leetcode.cn/problems/minimum-moves-to-equal-array-elements-ii/

class Solution {
public:
int minMoves2(vector<int>& nums) {
//中位数是最优解
//将nums中所有元素都变成nums数组中的中位数时,移动次数最少
//1.先排序
sort(nums.begin(),nums.end());
//2.累加数组所有数到中位数的距离
int ans = 0;
int mid = nums[nums.size()/2];
for(int i = 0;i<nums.size();i++)
{
ans += abs(nums[i] - mid);
}
return ans;
}
};
208. 实现 Trie (前缀树)
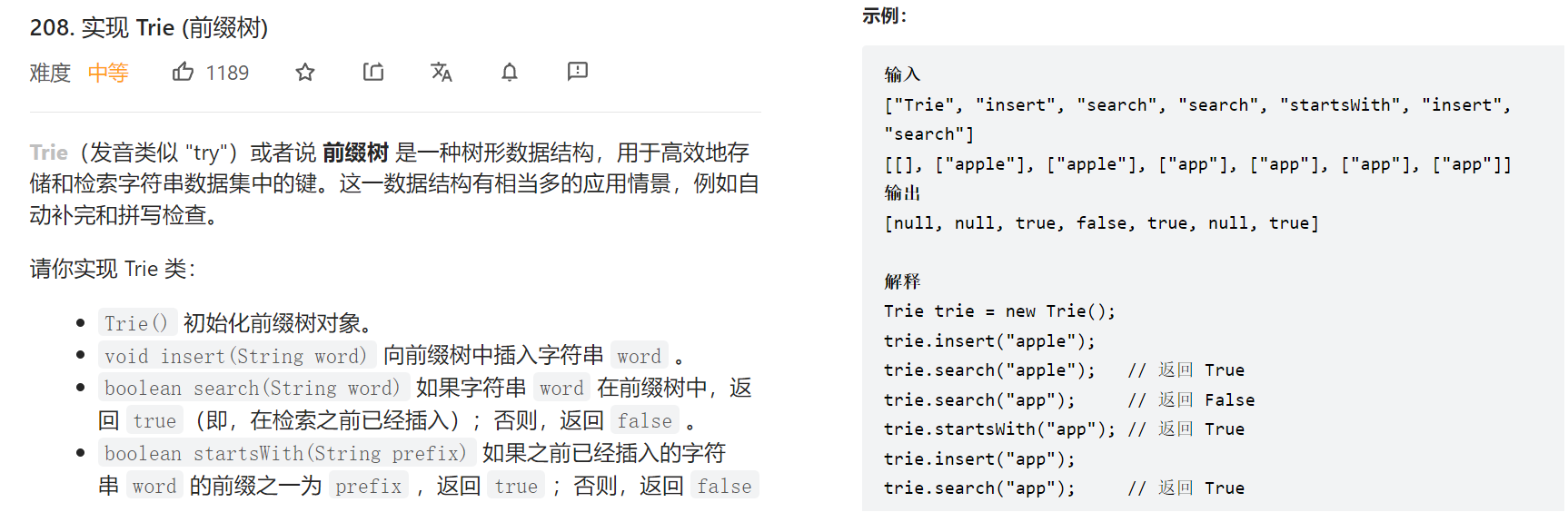
又称前缀树或字典树
每个节点包含以下字段:pass->标志多少个字符串创建的时候经过这个节点 end->多少个字符串以该节点结尾 nexts:指向子节点的数组/容器
插入字符串
我们从字典树的根开始,插入字符串。对于当前字符对应的子节点,有两种情况:
子节点存在:沿着指针移动到子节点,继续处理下一个字符
子节点不存在:创建一个新的子节点,记录在nexts数组的对应位置上,然后沿着指针移动到子节点,继续搜索下一个字符
重复以上步骤,直到处理字符串的最后一个字符,然后将当前节点标记为字符串的结尾
查找前缀
我们从字典树的根开始,查找前缀。对于当前字符对应的子节点,有两种情况:
子节点存在: 沿着指针移动到子节点,继续搜索下一个字符
子节点不存在: 说明字典树中不包含该前缀,返回空指针
重复以上步骤,直到返回空指针或搜索完前缀的最后一个字符若搜索到了前缀的末尾,就说明字典树中存在该前缀。此外,若前缀末尾对应节点的 end >0,则说明字典树中存在该字符串
哈希表unordered_map实现:
用map也可以实现
字母映射表next 的妙用就体现了,vector<TreeNode*> nexts ||unordered_map<char, TrieNode*> nexts; 中保存了对当前结点而言下一个可能出现的所有字符的链接,因此我们可以通过一个父结点来预知它所有子结点的值
struct TrieNode
{
TrieNode()
:end(0)
,pass(0)
{}
~TrieNode()
{
//释放哈希表的内容
for (auto& x : nexts)
{
delete x.second;//x是pair对象,我们要释放的是第二个成员,指针
x.second = NULL;
}
}
int end;
int pass;
unordered_map<char, TrieNode*> nexts;//字符-节点指针
};
class Trie {
public:
Trie() {
_root = new TrieNode();
}
void insert(string word) {
if (word == "") return;
TrieNode* cur = _root;//从根位置开始遍历
cur->pass++;//根节点的pass值++
for (int i = 0; i < word.size(); i++)
{
char ch = word[i];//字符
//检测cur->nexts[ch]得到的对应的节点,判断是否存在
if (cur->nexts[ch] == nullptr) //说明节点不存在,要新开辟一个节点
{
cur->nexts[ch] = new TrieNode();//相当于在哈希表新插入路径<ch,TrieNode*>
}
cur = cur->nexts[ch];
cur->pass++;
}
//最后一个位置的end值++
cur->end++;
}
bool search(string word) {
if (word == "") return false;
TrieNode* cur = _root;//从根位置往下找
for (int i = 0; i < word.size(); i++)
{
char ch = word[i];
if (cur->nexts[ch] == nullptr)
{
//说明该字符串不存在
return false;
}
cur = cur->nexts[ch];//到下一个位置考察
}
//如果结尾位置的end值>0说明字符串存在, 否则不存在
//不能直接return true,如:找abc 而只有abcd,这样就错了!
//因为c位置,end值不为1
return cur->end > 0;
}
bool startsWith(string prefix) {
if (prefix == "")
{
return 0;
}
TrieNode* cur = _root;//从根位置开始找
for (int i = 0; i < prefix.size(); i++)
{
char ch = prefix[i];
if (cur->nexts[ch] == NULL)//说明没有以pre为前缀的字符串
{
return 0;
}
cur = cur->nexts[ch];//到达下一个位置
}
return cur->pass;//返回pre最后一个字符对应的pass值,即多少个字符串构建的时候是以pre为前缀的
}
TrieNode* _root;
};
/**
* Your Trie object will be instantiated and called as such:
* Trie* obj = new Trie();
* obj->insert(word);
* bool param_2 = obj->search(word);
* bool param_3 = obj->startsWith(prefix);
*/
vector实现:
//前缀树的每个节点
struct TrieNode
{
TrieNode()
{
pass = 0;
end = 0;
nexts.resize(26, nullptr);
}
int pass;//pass:经过该节点的路径有几条
int end;//end:以该节点结尾的路径有几条
//下级的节点
vector<TrieNode*> nexts;//字符a-z 相对映射在vector,下标为0-25的位置
};
class Trie {
public:
Trie() {
root = new TrieNode();
}
void insert(string word) {
//如果words是空串就不插入
if (word == "") return;
TrieNode* cur = root;//从根节点出发
cur->pass++;//沿途节点的pass值要++
int path = 0;//标识当前字符应该映射在哪个位置
//遍历字符串
for (int i = 0; i < word.size(); i++)
{
path = word[i] - 'a';// 映射在vector的位置
//如果当前节点的vector中path下标的这个位置为空,就在path下标处新开辟一个节点
if (cur->nexts[path] == nullptr)
{
cur->nexts[path] = new TrieNode();//
}
cur = cur->nexts[path];//node去下一个节点
cur->pass++;//沿途节点的pass值++
}
//此时cur就是在字符串的结束节点处,该节点end值++
cur->end++;
}
bool search(string word) {
if (word == "") return false;
TrieNode* cur = root;
int path = 0;
for (int i = 0; i < word.size(); i++)
{
path = word[i] - 'a';
if (cur->nexts[path] == nullptr)
{
return false;
}
cur = cur->nexts[path];
}
return cur->end>0;
}
bool startsWith(string prefix) {
if (prefix == "") return 0;
TrieNode* cur = root;
int path = 0;
//遍历字符串
for (int i = 0; i < prefix.size(); i++)
{
path = prefix[i] - 'a';
//如果当前节点的nexts数组中path下标处的节点是空->字符串不存在
if (cur->nexts[path] == nullptr)
{
return 0;
}
cur = cur->nexts[path];//到达下一个位置
}
//返回此时字符串pre结尾节点的pass的值,就知道多少个字符串是以pre这个字符串作为前缀的
return cur->pass;
}
TrieNode* root;//前缀树的根节点
};
/**
* Your Trie object will be instantiated and called as such:
* Trie* obj = new Trie();
* obj->insert(word);
* bool param_2 = obj->search(word);
* bool param_3 = obj->startsWith(prefix);
*/
- 点赞
- 收藏
- 关注作者


评论(0)