基于前序遍历的无递归的树形结构的数据库表设计

目前常见的树形结构数据库存储方案有以下四种，但是都存在一定问题:
1)Adjacency List（邻接表）：每个节点仅记录父节点主键。优点是简单，缺点是访问子树需要递归遍历，对数据库压力大（即使是支持递归SQL的数据库)。
2)Path Enumerations( 路径枚举)：用一个字符串记录当前节点所在路径。优点是查询方便，缺点是占用空间大，查询需要使用like模糊方法，效率低，插入新记录时要手工更改此节点以下所有路径，维护不便。
3)Closure Table(闭包表)：专门一张表维护Path，缺点是占用空间大，操作不直观。
4)Nested Sets (嵌套集)：记录左值和右值，优点是查询子树无需递归，缺点是非常复杂、难操作。

本文介绍的基于树形结构的前序遍历序列方法，示意图如下：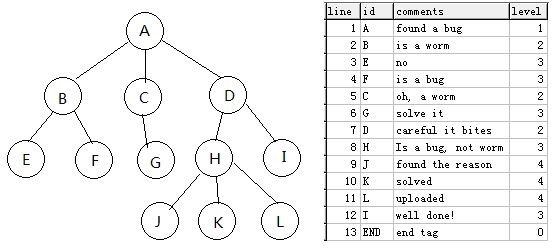  


如上图左边的树结构，映射在数据库里的结构见右图表格，注意整个表格是一个排好序的树结构的前序遍历序列,相同节点深度的排序以line为准。 表格的最后一行(或每个根节点)必须有一个END标记，level设为0，上表中的ID为主键，Level为树节点的深度。在以上基础上，只要一句SQL,就可以无递归查询出任意节点的所有子树节点, 比某些数据自带的基于递归原理的查询更高效。 假设节点的行号为X,level为Y,则查询整个子树的SQL为: 

select * from tb where line>=X and line<(select min(line) from tb where line>X and level<=Y)

例如获取D节点及其所有子节点： 

select * from tb where line>=7 and line< (select min(line) from tb where line>7 and level<=2)

它依据的原理很简单：按树结构的前序遍历序列存储的树结构，判断它的所有子结点，只要从这个节点开始往下划竖线，竖线右边的全是它的子节点，直到碰到竖线上或竖线左边出现非空值则终止，原理图如下：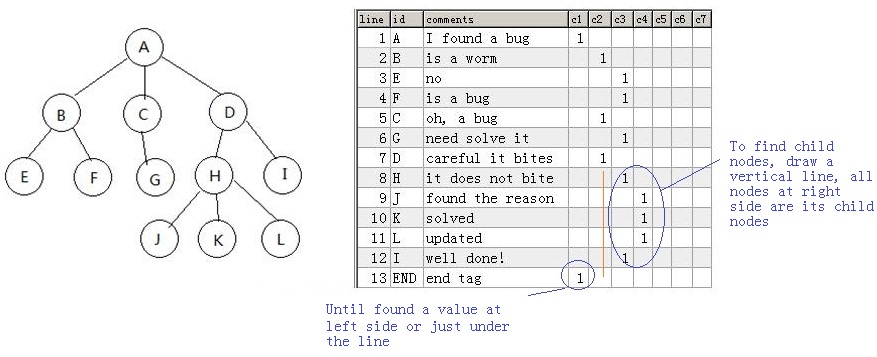


这种方案的优点是查询高效，删除高效（只需要删除当前行即可，虽然会造成line字段的跳号，但是不影响使用），插入节点也很简单，只需要2行简单的SQL即可，例如要在line=9和line=10的两个节点之间插入一个新节点，则新节点行号应为10,原行号为10的将变为11, SQL操作为:

update tb2 set line=line+1 where line>=10; //把10以后的所有行号加1
insert into tb (line,id,level) values (10,'T',4); //执行插入新节点操作

虽然影响的行数非常多，但是理解和维护都非常简单。 如果担心插入操作对性能的影响，还可以将行号跳号设计(如按100000跳号)，新的节点可以插入在两个节点的空号区中段(如果节点间存在空号区)，这样可以很大程序上消除进行加1操作的概率。

这种方案的缺点是当需要移动节点时，必须维护整张表的前序遍历排序顺序，必要时要进行整张表或子树的重排序, 这是一个很耗时的工作(其它三种方案Path Enumerations/Closure Table/Nested Sets也有这个缺点），这是不可避免的，是以始终维护一个索引为代价换取查询性能的提高。因此它最适合只有增删查操作，但是很少有移动节点的场合。

总结：这种方案最适合的场合是树的深度很深(可以超过上百万)，不经常移动节点、对查询速度要求极高的场合(因为无递归)。

本文实际上可以抽象成一种利用前序遍历给多叉树建查询索引的方案，即使在没有数据库存在的情况下，也是有可能在程序中应用到这种方案的，只要将SQL中的查询功能改成手工进行数组遍历即可。
另外，数据库开发者也可以考虑，对于邻接表模式(即只有id和pid两个关键字段)存储的树结构, 可以用这种方法创建一个内部索引，将level和line作为数据库表的隐藏字段，这样用户就可以不用手工维护level、line以及维护前序遍历排序这些与业务无关的操作，这才是最人性化的使用方式。