机器学习Gradient Descent(梯度下降) + Momentum(动量)寻找局部最优解Local Minima的过程
Gradient Descent(梯度下降) + Momentum(动量)
上次 这里 介绍了Gradient Descent寻找最优解的过程
学习到发现还有一个算法就是加上Momentum(动量,就是上一次Gradient Descent后的步长值)来作为下一次更新位置的参数,这样来寻找局部最优解Local Minima的话,会比单独使用梯度下降法来求解效果更好,有一点像粒子群算法。
Movement:最后一步的移动目前是最小的梯度
- 首先
同梯度下降法一样,找到一点起始点 θ 0 θ^0 θ0,此时的位移(Movement)为0,故 M 0 = 0 M^0=0 M0=0.
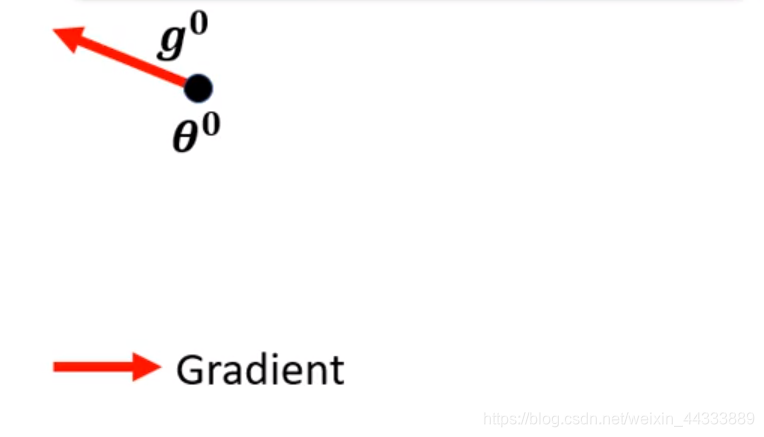
- 紧接着
Gradient Descent来计算 g 0 g^0 g0,再计算下一步的 M 1 = λ M 0 − δ g 0 M^1=λM^0-δg^0 M1=λM0−δg0
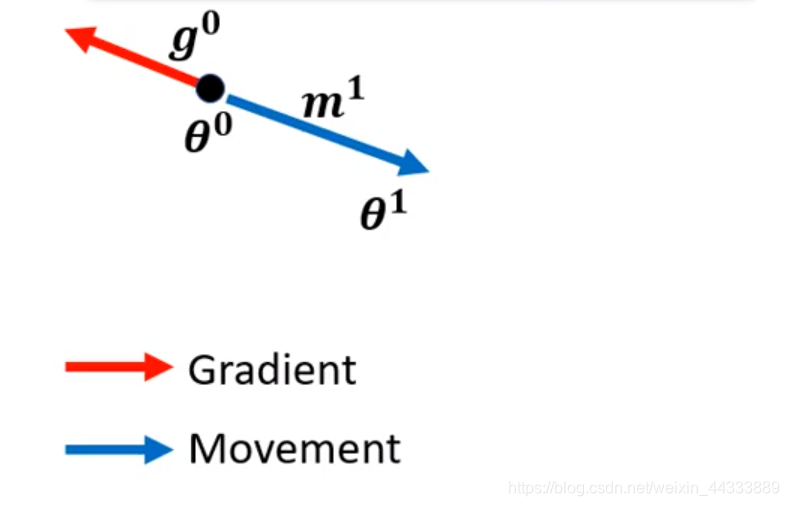
由于加了动量,故不再按照梯度下降法的反方向寻找Local Minima了
- 然后
移动 θ 1 = θ 0 + M 1 θ^1=θ^0+M^1 θ1=θ0+M1,再计算 g 1 g^1 g1,再移动 M 2 = λ M 1 − δ g 1 M^2 =λM^1-δg^1 M2=λM1−δg1
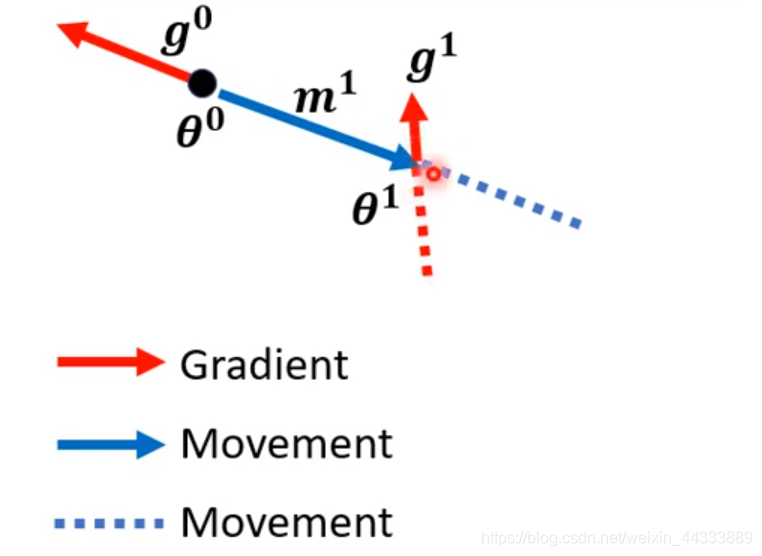
再移动 θ 2 = θ 1 + M 2 θ^2=θ^1+M^2 θ2=θ1+M2
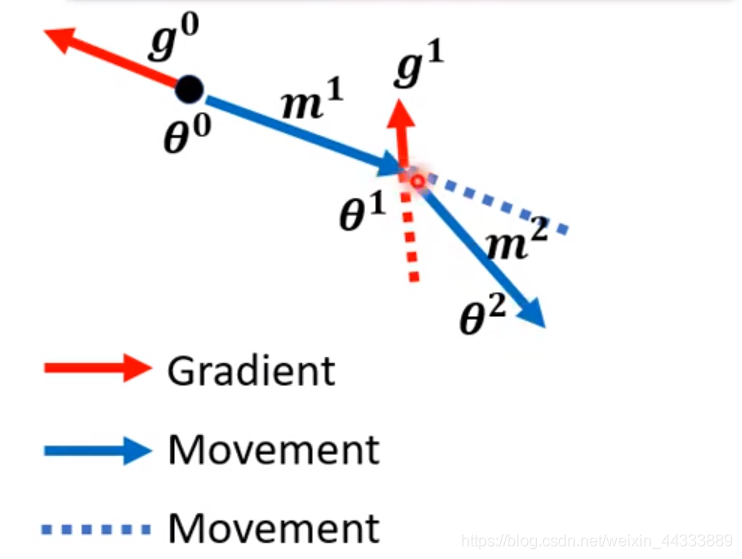
注意,此时的 θ 2 θ^2 θ2为Gradient Descent(梯度下降) + Momentum(动量)以后的方向,这样的话寻找 Local MInima会更加精确,避免overfitting,和共轭方向法类似。
然后,以此类推求下去
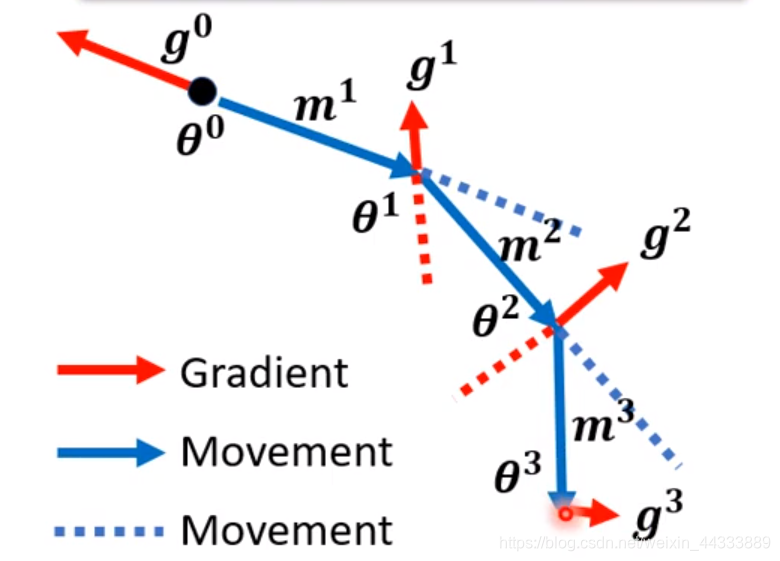
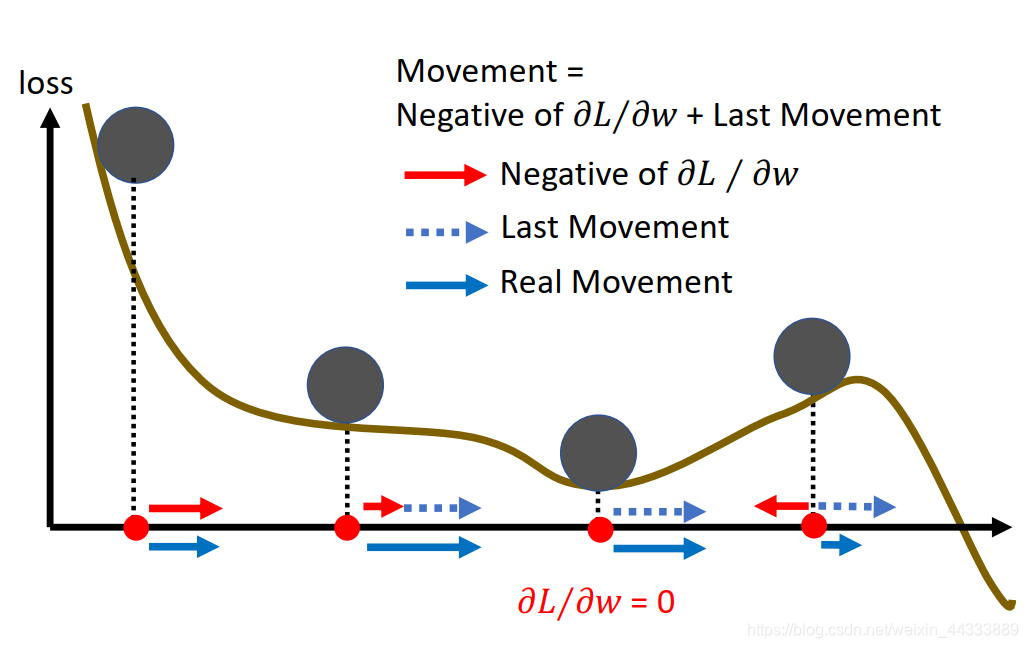
具体地,如下图,加上动量后,寻找的过程可能会比单一梯度下降慢,就比如在遇见第一个Local MInima的时候,Gradient Descent或许就会停下来了,而Gradient Descent(梯度下降) + Momentum(动量)呢,当上一步的Movement和 g x g^x gx的大小相等,方向相反,那么会被抵消;若Movement大于 g x g^x gx的值,那么会继续往后面去寻找局部最优解,但是最终,还是会回到最好的局部最优解位置来。
Deep Learning Fitting!!!
ღ( ´・ᴗ・` )
❤
学习DeepLearning坚持!30天计划!!!
打卡 第 1 /30 Day!!!
『
你说过,人最大的敌人是自己。
』
文章来源: blog.csdn.net,作者:府学路18号车神,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/weixin_44333889/article/details/119191209
- 点赞
- 收藏
- 关注作者


评论(0)